Высшая математика 

Методические указания

назад

Задача 1.

Теоретическое введение

Функцией переменной величины , называется величина такая, что каждому значению , принадлежащей некоторой области , соответствует единственное значение величины .

Обозначение: .

– область определения функции, – аргумент.

– область изменения функции, – значение;

Функия может быть задана аналитически, таблично, графически.

Основными элементарными функциями являются:

  1. степенные (, где – произвольное число)

  2. показательные (, , )

  3. логарифмические (,, )

  4. тригонометрические (, , , )

  5. обратные тригонометрические (,,, )

Композиция (суперпозиция) двух функций и есть функция, в которой аргументом одной из данных функции, является значение другой функции. Обозначение: и .

Сложная функция есть композиция двух и более функций.

Элементарная функция есть функция, полученная из основных элементарных функций с помощью арифметических действии и композиции.

Целью математического анализа является изучение различных функций, их свойств, и операций связанных с функциями.

Функция называется четной, если для всех своих аргументов.

Функция называется нечетной, если для всех своих аргументов.

Число называется пределом функции при , стремящемся к и обознается , если при неограниченном приближении к , неограниченно приближается .

Свойства пределов:

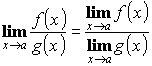  1. Передел суммы двух функций равен сумме пределов этих функций, если они существуют:

  2. Предел произведения функции равен произведению пределов, если они существуют:

  3. Предел частного двух функций равен частному пределов, если они существуют, и предел знаменателя не равен нулю: , при
.

Обычно , например:

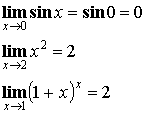
Однако, иногда значение не входит в область определения функции . В этом случае имеются различные методы вычисления пределов:

Выделение общего множителя

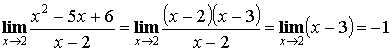
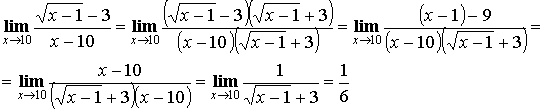
    3. Выделение главной части

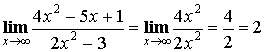
    5. Использование замечательных пределов

    Первый замечательный предел:

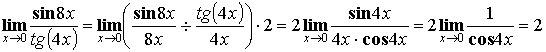
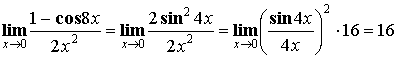
    7. Второй замечательный предел: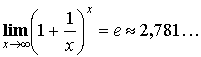

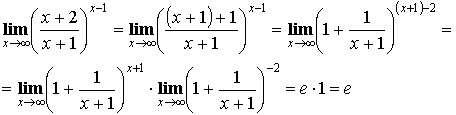
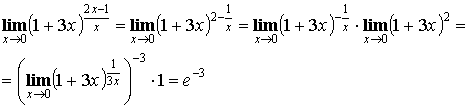
    8.  

Задача 2.

Теоретическое введение

Производная или от данной функции есть предел отношения приращения функции к соответствующему приращению аргумента, когда приращение аргумента стремится к нулю: или

Механический смысл производной – скорость изменения функции.

Геометрический смысл производной – тангенс угла наклона касательной к графику функции:

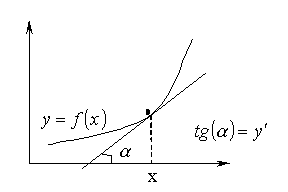
Правила дифференцирования:

  1. Производная постоянной величины равна 0.

  2. Производная суммы равна сумме производных.

  3. Производная произведения:

  4. Производная частного:

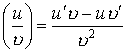
Производная сложной функции:

Производная от сложной функции по независимому аргументу равна производной от по промежуточному аргументу , умноженной на его производною по независимой переменной .

Примеры:

  1. ;

  2. ;

  3. ;

 

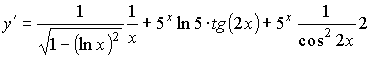
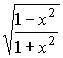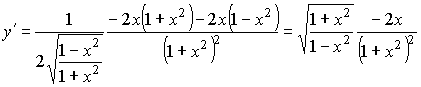
Методика решения задачи 3 (исследование функции) см. примеры из конспекта лекций.

Задача 4.

Найти неопределенные интегралы:

а) ;

Решение: введем переменную . Тогда

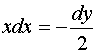; . Сделаем замену:

.

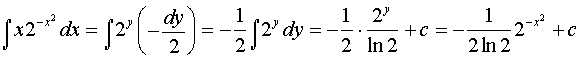б) ;

Решение: используем метод интегрирования по частям:

.

Обозначим: . Тогда .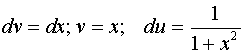

Задача 5.

Вычислить площадь фигуры, ограниченной линиями:

и .

Решение:

Найдем точки пересечения графиков данных функций. Для этого приравняем функции и решим уравнение

Итак, точки пересечения и .

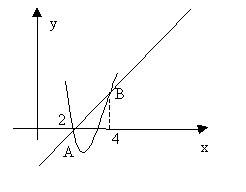
Площадь фигуры найдем, используя формулу

.

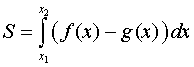В нашем случае

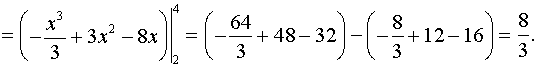
Ответ: площадь равна (квадратных единиц).

назад