8.3. Основные структуры алгоритмов

Основные структуры алгоритмов — это ограниченный набор блоков и стандартных способов их соединения для выполнения типичных последовательностей действий. Приводимые ниже структуры рекомендуются при использовании так называемого структурного подхода к разработке алгоритмов и программ. Структурный подход предполагает использование только нескольких основных структур, комбинация которых дает все многообразие алгоритмов и программ.

К основным структурам относятся:

1. Следование. Последовательное размещение блоков и групп блоков. В программе реализуется последовательным размещением операторов.

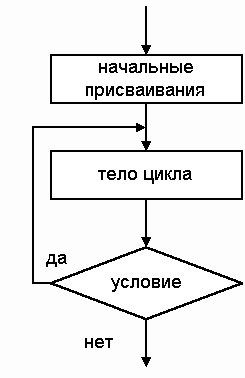
2. Ц и к л До (рис. 8.3). Применяется при необходимости выполнить какие-либо вычисления несколько раз до выполнения некоторого условия. Особенность этого цикла в том, что он всегда выполняется хотя бы один раз, так как первая проверка условия выхода из цикла происходит после того, как тело цикла выполнено. Тело цикла — а последовательность действий, которая выполняется многократно (в цикле). Начальные присвоения — задание начальных значений тем переменным, которые используются в теле цикла.

Рис. 8.3	Рис. 8.4

На естественном языке циклу До соответствует последовательность операторов:

1 Операторы начальных присвоений

2 Операторы тела цикла

3 Если условие идти к 2

Цикл, использованный в приведенном выше примере, это цикл До.

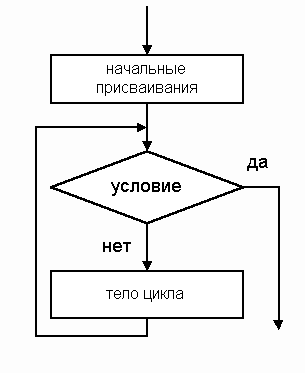
3. Цикл Пока (рис. 8.4). Цикл Пока отличается от цикла До тем, что проверка условия проводится до выполнения тела цикла, и если при первой проверке условие выхода из цикла выполняется, то тело цикла не выполняется ни разу.

На естественном языке циклу Пока соответствует последовательность операторов:

1 Операторы начальных присвоений

2 Если условие идти к 5

3 Операторы тела цикла

4 Идти к 2

5 ...

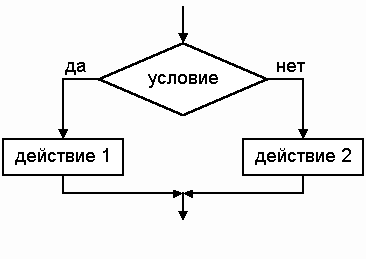
4. Разветвление (рис. 8.5). Применяется, когда в зависимости от условия нужно выполнить либо одно, либо другое действие. Действие 1 или действие 2 может в свою очередь содержать несколько этапов.

Рис. 8.5	Рис. 8.6

На естественном языке разветвлению соответствует последовательность операторов:

1 Если условие идти к 4

2 Операторы действия 2

3 Идти к 5

4 Операторы действия 1

5 ...

5. Обход (рис. 8.6). Частный случай разветвления, когда одна ветвь не содержит никаких действий.

6. Множественный выбор (рис.8.7). Является обобщением разветвления, когда в зависимости от значения переменной (I) выполняется одно из нескольких действий. При I=1 выполняется действие S1,при I=2— действие S2 и т. д.

Особенностью всех приведенных структур является то, что они имеют один вход и один выход, и их можно соединять друг с другом в любой последовательности. В частности, каждая структура может содержать любую другую структуру в качестве одного из блоков.

Обычно при составлении схемы блоки размещаются друг под другом в порядке их выполнения. Возврат назад осуществляется только на циклах. Это дает простую и наглядную структуру алгоритма, по которой далее легко составить программу.

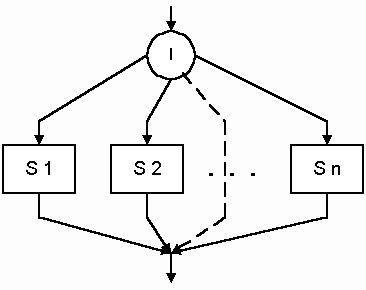
Рис. 8.7

Одним из приемов разработки алгоритма решения более сложных задач является метод пошаговой детализации, когда первоначально продумывается и фиксируется общая структура алгоритма без детальной проработки отдельных его частей, но при этом также используются лишь основные структуры алгоритмов. Блоки, требующие дальнейшей детализации, обозначаются пунктирной линией. Далее прорабатываются (детализируются) отдельные блоки, не детализированные на предыдущем шаге. То есть на каждом шаге разработки уточняется реализация фрагмента алгоритма (или программы), и, таким образом на каждом шаге мы имеем дело с более простой задачей. Полностью закончив детализацию всех блоков, мы получим решение всей задачи в целом. Описанный метод пошаговой детализации называется также программированием сверху вниз.

В некоторых случаях стремление во что бы то ни стало остаться в рамках структурного подхода приводит к необоснованному усложнению программы и потере ее наглядности и естественности. Если учесть, что структурное программирование имеет целью не подчинить программы каким-то правилам, а сделать их более удобными для восприятия, то в ряде случаев оказывается целесообразным отдать предпочтение ясности и естественности программы.

Упражнения. Составить схему и программу на естественном языке для решения задач, используя типовые структуры алгоритмов и их простые сочетания.

Выполнить составленную программу при заданных исходных данных, фиксируя значения изменяемых переменных в ячейках памяти и с помощью трассировочной таблицы. Для каждого из заданных наборов данных программу нужно выполнять заново, начиная с первого оператора.

Упражнение 1. Разделить натуральное число n на натуральное число m, получить в качестве результата частное от деления k и остаток l, т. е. представить число n в виде

n = k m + l ,

где l < m, k – целое. Операцию деления не использовать.

Решение. Операцию деления можно представить как последовательность вычитании делителя из делимого. Тогда количество вычитаний будет частным от деления k. При этом последовательные вычитания нужно проводить до тех пор, пока результат вычитания не станет меньше делителя. Тогда эта последняя разность и будет остатком от деления l.

Далее приводится схема алгоритма (рис. 8.8) и программа на естественном языке для решения этой задачи.

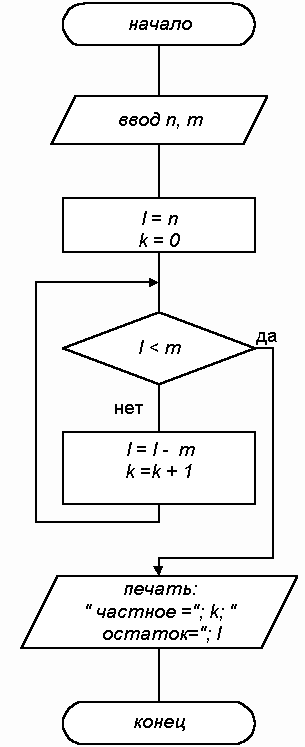
Рис. 8.8

Программа “Деление двух натуральных чисел”. Исходные данные: n, m - натуральные числа. Результат: k, l.
1 задать значения n, m
2 l = n
3 k = 0
4 если l < m идти к 8
5 l = l — m
6 k = k +1
7 идти к 4
8 закончить вычисления

Обратите внимание на то, что проверка условия выхода из цикла проводится до входа в цикл (цикл Пока) и при n < m остается k = 0.

Выполнить программу при: 1) n = 15, m = 5; 2) n = 14, m = 5; 3) n = 3, m = 5;

Упражнение 2. Задано число х. Вычислить функцию знака числа

Решение. Схема алгоритма приводится на рис. 1.9. Алгоритм представляет собой разветвление, содержащее в одной из ветвей еще одно разветвление.

Рис. 8.9

Программа “Вычисление знака числа”. Исходные данные: х — любое число. Результат: S.

1. задать значение х
2. если х < 0 идти к 8
3. если х = 0 идти к 6
4. S = 1
5. идти к 9
6. S = 0
7. идти к 9
8. S = -1
9. закончить вычисления

Обратите внимание на использование оператора “идти к N” (операторы 5, 7) в этой программе. Он позволяет обойти одну из ветвей разветвления, если выполнена другая.

Выполнить программу при: 1) х = -6; 2) х = 0; 3) х = 12.

Упражнение 3. Выбрать максимальное из двух чисел х, у и присвоить его значение переменной u.

Решение. Для решения этой простой задачи будем просматривать числа по очереди. Пока мы “видим” только первое число х, будем считать его максимальным и присвоим u значение х (u = х). Затем и сравним со вторым числом у, и если окажется, что значение u меньше у, то u присвоим новое значение, иначе u оставим без изменения. Схема алгоритма приведена на рис. 1.10.

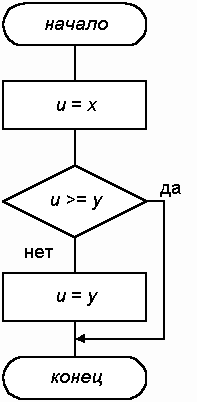
Рис. 8.10

Программа “Нахождение максимального из двух чисел”. Исходные данные: х, у — любые числа. Результат: u - максимальное из х, у.

1. задать значения х, у
2. u = х
3. если u у идти к 5
4. u = у
5. закончить вычисления

Следует обратить внимание на характерный прием, используемый в приведенной программе. Значение переменной u в результате выполнения программы будет равно либо х, либо у. Одно из этих значений и присваивается переменной u в начале программы (u = х). Далее, переменная u изменяет свое значение, только если х < у. Если же х у, то значение u сохраняется без изменений.

Идея, лежащая в основе этого алгоритма, позволяет единообразными действиями найти максимальное из трех и т.д. чисел.

Программа “Нахождение максимального из трех чисел”. Исходные данные: х, у, z - любые числа. Результат: u —максимальное из х, у, z.

1. задать значения х, у, z
2. u = х
3. если u у идти к 5
4. u = y
5. если u z идти к 7
6. u = z
7. закончить вычисления

Выполнить программу при: 1) х = 8, y = 12, z = 6; 2) х = 5, y = 3, z = 4; 3) х = 6, y=2, z = 13.

Упражнение 4. В переменную х по очереди помещаются (вводятся) 10 чисел. В переменной Р получить максимальное из этих чисел.

Решение. Если до входа в цикл переменной Р присвоить значение первого введенного числа х, то в цикле для очередного значения х нужно проверять условие P x, и если оно не выполняется, то заменить старое значение Р на новое, равное текущему значению х. После чего в х вводится следующее значение. Алгоритм представляет собой цикл До с обходом внутри цикла. Схема алгоритма представлена на рис. 8.11 в двух вариантах.

В первом варианте (рис. 8.11а) имеются два блока ввод х. Первый из них выполняется только один раз для ввода первого числа, которое используется для задания первоначального значения Р, и если остальные числа окажутся не больше первого, то Р сохранит это первое значение. Второй блок ввод х выполняется многократно (в цикле), и каждый раз осуществляется ввод в переменную х (задание переменной х значения) очередного из заданных десяти чисел.

Второй вариант (рис. 8.116) составлен для случая поиска максимального из десяти положительных чисел. Если известно, что все вводимые числа будут больше какого-либо заданного значения (в данном случае больше нуля), то первоначально Р можно задать таким, чтобы первое введенное значение х его обязательно превзошло (например, вначале присвоить Р любое отрицательное число). Тогда ввод первого значения х можно также осуществлять в цикле.

Программа “Нахождение максимального из десяти положительных чисел”.

1. Р = -1
2. i = 1
3. задать очередное значение х
4. если P x идти к 6
5. Р = x
6. i = i +1
7. если i 10 идти к 3
8. закончить вычисления

Выполнить программу для следующего набора чисел: 3, 18, 24, 8, 11, 6, 12, 19, 44, 23.

Упражнение 5. Задано n троек чисел a, b, c. Вводя их по очереди и интерпретируя как длины сторон треугольника, определить, сколько троек может быть использовано для построения треугольника (числа a, b, c при вводе расположены в порядке возрастания a b c). Результат получить в переменной k.
Указание. По трем сторонам с длинами a, b, c (a bc ) можно построить треугольник, если с<а+b.

Алгоритм решения задачи представлен на рис. 8.12.

Для каждой тройки чисел проверяется условие с³ a+b , и если оно не выполняется (треугольник может быть построен), то значение k, увеличивается на 1. До входа в цикл, пока ни одна тройка чисел не введена и не проверена на возможность построения треугольника, k полагается равным 0.

Программа “Определение числа треугольников”.

1. задать значение n
2. k = 0
3. i = 1
4. задать очередной набор a, b, c
5. если сa+b идти к 7
6. k = k + 1
7. i = i + 1
8. если i n идти к 4
9. закончить вычисления

Выполнить программу для пяти (n = 5) троек чисел:

1. 6, 12, 3; 2) 5, 2, 2; 3)11, 6, 2; 4) 1, 6, 3; 5) 4, 6, 2.

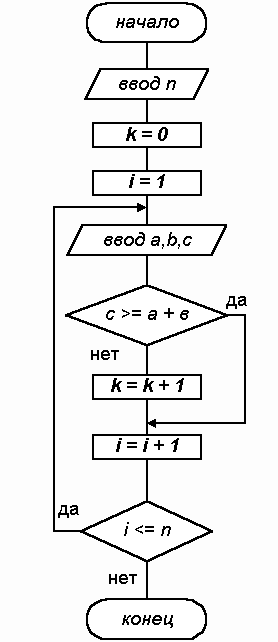
Рис. 8.12