2.1. Краткие теоретические сведения

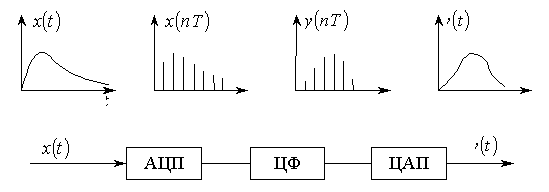
Система дискретной обработки непрерывных (аналоговых) сигналов (рис. 2.1.) получила широкое распространение в связи с высоким качеством цифровой обработки дискретных последовательностей. Преобразователи "аналог – цифра" (АЦП) и "цифра – аналог" (ЦАП) являются устройствами сопряжения цифрового процессора – в данном случае цифрового фильтра (ЦФ) – с аналоговой частью канала связи.

Рис. 2.1

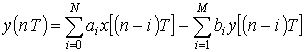,                                                       (2.1)

где  – коэффициенты, определяемые параметрами ЦФ в направлении прямого прохождения сигнала,

 – коэффициенты, определяемые параметрами ЦФ в цепи обратной связи.

Согласно (2.1), дискретная система состоит из элементов задержки сигналы, умножителей и сумматоров. Разностному уравнению дискретной системы соответствует дифференциальное уравнение аналоговой системы.

Дискретная система без обратных связей называется нерекурсивным ЦФ. Схема нерекурсивного ЦФ общего вида приведена на рис. 2.2а.

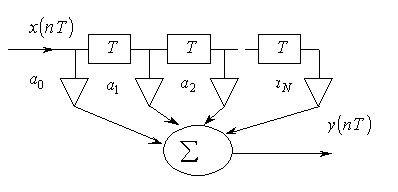
Рис. 2.2а

Соответствующее разностное уравнение можно записать непосредственно по схеме или согласно (2.1) :

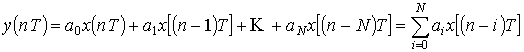
или в сокращенной форме записи

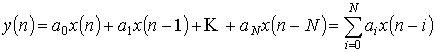
Дискретная система с ОС называется рекурсивным ЦФ. Схема рекурсивного ЦФ общего вида приведена на рис 2.2б. функционирование такого фильтра описывается разностным уравнением (2.1).

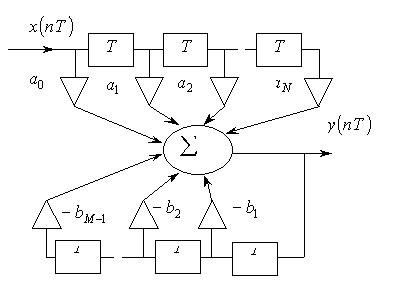
Рис. 2.2б

Разностное уравнение является основой расчета ЦФ во временной области. Во временной области к ЦФ предъявляются требования относительно импульсной характеристики фильтра . Для нерекурсивного ЦФ импульсная характеристика в соответствии с определением имеет вид последовательности

,

поэтому поставленная задача решается выбором соответствующих значений коэффициентов в отводах фильтра .

Для рекурсивного ЦФ, содержащего  прямых  обратных отводов, импульсная характеристика запишется так

                                                           (2.2)

где  – дискретная  – функция.

В наиболее простом случае можно потребовать, чтобы  первых отсчетов в (2.2), причем , совпадали бы с  первыми отсчетами требуемой последовательности. В этом случае, согласно (2.2), получается система из  уравнений, в которой  последних уравнений не содержат коэффициентов , что позволяет вычислить коэффициенты . Затем производится расчет коэффициентов  из системы  первых уравнений.

Расчет ЦФ в частной области имеет ряд особенностей и первая их них определяется тем обстоятельством, что преобразование Фурье или Лапласа применительно к (2.1) приводит к передаточной функции трансцендентного вида. В результате расчет ЦФ резко усложняется. Существенных упрощений можно добиться, если частное описание ЦФ осуществлять в области  – изображений.

Формулы прямого и обратного  – преобразования имеют вид

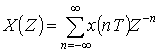
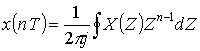                                                                         (2.3)

Частотные переменные  и  связанны соотношением

                                                                                                     (2.4)

В соответствии с (2.4), левая полуплоскость комплексного переменного  преобразуется во внутреннюю часть единичного круга на плоскости , а правая полуплоскость – во внешнюю часть круга (рис. 2.3); мнимая ось на плоскости  переходит в окружность единичного радиуса на плоскости .

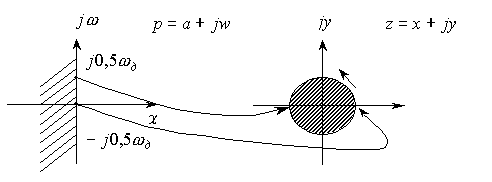
Рис. 2.3

 – изображения дискретных сигналов и системных характеристик являются рациональными функциями, что упрощает решение задач анализа и расчета ЦФ.

Если применить  – преобразование к (2.1), то можно получить выражение для передаточной функции рекурсивного ЦФ

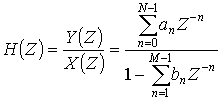,                                                                    (2.5)

где . Соответствующее выражение для нерекурсивного ЦФ

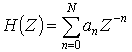
Определить передаточную функцию ЦФ можно  непосредственно по схеме; коэффициент передачи элемента задержки равен  в соответствии с теоремой запаздывания и формулой (2.4).

По известным  – изображениям – , ,  – простой заменой

                                                                                                    (2.7)

Для формирования требуемых характеристик можно применить как нерекурсивный, так и рекурсивный ЦФ. Но каждый из фильтров имеет свои особенности. Нерекурсивный ЦФ имеет при прочих равных условиях больше отводов, то есть получается более сложным. С другой стороны, нерекурсивный ЦФ позволяет получить линейную фазу при произвольной АЧХ, такой фильтр всегда устойчив и проще в настройке, эффекты конечной разрядности кодовых слов меньше сказываются на качественных показателях фильтра.

Рассмотрим расчет нерекурсивных ЦФ с линейной фазой, получивших наибольшее распространение среди устройств с нерекурсивной реализацией.

Нерекурсивные ЦФ с линейной ФЧХ получается при условии симметричной (рис. 2.4а) или антиметричной (рис. 2.4б) импульсной характеристики фильтра.

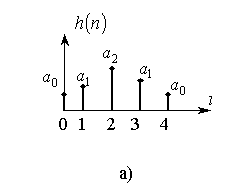
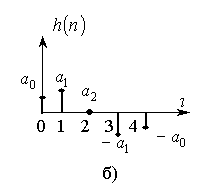
Рис. 2.4

В случае симметричной характеристики фаза фильтра определяется выражением

,                                                                (2.8)

где  – число отсчетов, включая нулевой отсчет,

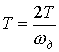,  – частота дискретизации.

АЧХ выражается в форме ряда Фурье, содержащего только косинусы.

В случае антиметричной импульсной характеристики

                                                             (2.9)

АЧХ выражается в форме ряда Фурье, содержащего только синусы.

Пусть, например, импульсная характеристика имеет вид, показанный на рис. 2.4а. Тогда

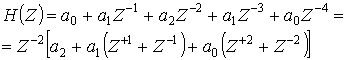
Отсюда, после замены по формуле (2.7) и очевидных преобразований

.

Следовательно,

,

Как видно из примера, отсчеты импульсной характеристики фильтра численно равны коэффициентам ряда Фурье, выражающего АЧХ фильтра. Этот факт используется для расчетов коэффициентов ряда Фурье, поскольку отсчеты во временной области и отсчеты в частной области связаны формулами дискретного преобразования Фурье (ДПФ)

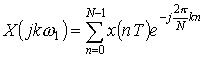
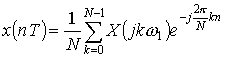,                                                                   (2.10)

где ,

 – интервал между частотными выборками.

Наибольшее распространение получили два метода расчета нерекурсивных ЦФ: метод рядов Фурье и метод частотной выборки.

Рассмотрим основные этапы расчета по методу рядов Фурье. 

1.     Выбрать тактовую частоту  с таким расчетом, чтобы требуемая характеристика разместилась в диапазоне .

2.     Продлить требуемую частотную характеристику на весь диапазон  четным и нечетным образом, поскольку частотная характеристика ЦФ есть функция периодическая. Необходимое число первых членов ряда Фурье получается по возможности наименьшим, если учесть особенности требуемой АЧХ.

Например.

a)     Падающий  характер АЧХ (рис. 2.5а,б). Следует выбрать симметричную импульсную характеристику ЦФ (ряд косинусов). На рис. 2.5а АЧХ продлена нечетным образом (постоянной составляющей не будет, поэтому  нужно взять четными), на рис. 2.5б АЧХ продлена четным образом (постоянная составляющая  присутствует, то есть  – нечетное)

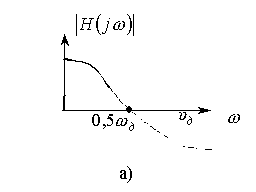
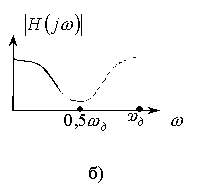
Рис. 2.5

b)    Нарастающий характер АЧХ (рис. 2.5в,г). Следует взять вариант ЦФ с антиметричной импульсной характеристикой (ряд синус). На рис. 2.5в АЧХ продолжена четным образом ( – четное), на рис. 2.5г – нечетным образом ( – нечетное).

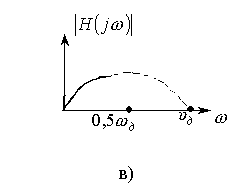
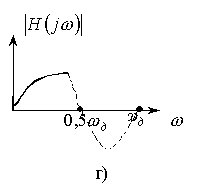
Рис. 2.5

3.     Задаться числом  частотных выборок (включая нулевую) в диапазоне . Чем больше , тем выше точность аппроксимации, но увеличивается сложность ЦФ.

4.     Определить фазу частотных выборок по формулам (2.8), (2.9) и рассчитать отсчеты импульсной характеристики ЦФ , то есть коэффициенты ряда, по формуле обратного ДПФ (2.10).

5.     Составить схему ЦФ, в которой , и определить передаточную функцию . Осуществить переход  в соответствии с (2.7) и выполнить поверочный расчет частотных характеристик ЦФ.

Другое название метода рядов Фурье – метод взвешивания. Дело в том, что на участках резкого перехода частотных характеристик от одного значения к другому качество аппроксимации резко ухудшается за счет эффекта Гибсса, поэтому значение  берутся с определенным весом. Весовая функция  – сглаживающая "окно" (рис. 2.4в) – существенно уменьшает амплитуду колебаний аппроксимирующей функции вблизи крутых изгибов требуемой характеристики. Существует различные типы весовых функций, например, "окно"  Хемминга.

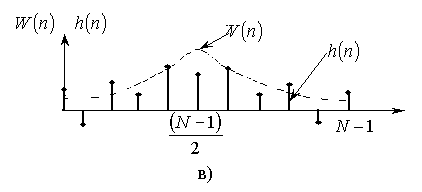
Рис. 2.4

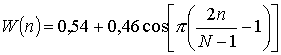                                                       (2.11)

Реализация устройств, передаточная функция которых в области реальных частот должна содержать мнимую единицу в качестве множителя (дифференциаторы, интеграторы, преобразователи Гильберта), осуществляется, как правило, по схеме нерекурсивного ЦФ. В этом случае следует брать импульсную характеристику антиметричного типа.

Метод частотной выборки

Расчет по методу частотной выборки совпадает с расчетом по методу рядов Фурье. Различие состоит в способах улучшения качества аппроксимации на участках разрыва частотных характеристик. В окрестности разрыва (переходная область) значения частотных выборок оптимизируются с таким расчетом, чтобы улучшить качество аппроксимации в смысле поставленных целей. Например, оптимизация выборок, попавших в переходную область АЧХ для идеального ФНЧ позволяет увеличить минимум затухания в полосе непропускания: если в переходную область попадает одни отсчет, то можно получить минимум затухания порядка 50 дБ, два отсчета – 70 дБ, три отсчета – 90 дБ.

Применение сглаживающих "окон" и оптимизации частотных выборок в переходной области позволяет получить вариант аппроксимации, близкий к оптимальному.

Рассмотрим расчет рекурсивных фильтров.

Нерекурсивный ЦФ не имеет аналогов в виде цепи RLC. Рекурсивный ЦФ наоборот имеет много общего с обычными фильтрами. Например,  импульсная характеристика рекурсивного ЦФ и непрерывного фильтра есть функция бесконечной протяженности. Поэтому расчет рекурсивного ЦФ, по – возможности, стремятся свести к расчету аналогового фильтра, что позволяет воспользоваться обширной литературой по расчету аналоговых фильтров.

Прямой переход от одного типа фильтров к другому через системные характеристики согласно (2.4) или (2.7), то есть

невозможно, так как в результате перехода передаточная функция становится трансцендентной, а значит физически нереализуемой. Поэтому получили распространение различные способы приближенного перехода, среди которых чаще применяется метод билинейного преобразования. Метод билинейного преобразования основан на замене точного равенства (2.4) приближенным равенством

                                                                                              (2.12)

Подстановка (2.12) в выражение для  приводит к рациональной функции , что требуется по условиям физической реализуемости. Погрешности, возникающие за счет приближения в (2.12), можно учесть в процессе проектирования.

Основные этапы расчеты по методу билинейного преобразования.

1.     Выполнить пересчет по точкам требуемых частотных характеристик ЦФ в соответствующие характеристики АФ по формуле, следующей из (2.12)

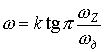,                                                                                          (2.13)

где  – частота для АФ,

 – частота для ЦФ.

Значение коэффициента  может быть любым, поэтому  можно выбрать, например, по соображениям нормирования оси частот.

2.     Решить задачу аппроксимации для АФ и сформировать передаточную функцию .

3.     Осуществить переход  в соответствии с (2.12).

4.     Проверить  на устойчивость: полюсы  должны находиться внутри единичного круга на плоскости . Устойчивость не выполняется в исключительных случаях. Удовлетворительного решения можно добиться, например, допустимой коррекцией исходных данных, параметров аппроксимации, величины тактовой частоты.

5.     Осуществить реализацию .

Реализация рекурсивного ЦФ по схеме общего вида (рис. 2.2б) применятся редко: схема общего вида чувствительна к ошибкам округления в умножителях ЦФ. Поэтому  чаще применяется параллельная или каскадная реализация.

Для параллельной реализации требуется представление  в виде суммы простых дробей

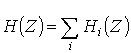                                                                                     (2.14)

Для каскадной реализации требуется представление   в виде произведения простых сомножителей

                                                                                     (2.15)

Простейшие передаточные функции  в общем случае второго порядка, так как комплексно-сопряженную пару полюсов или нулей разделять нельзя. Поэтому общий вид такой функции

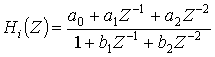                                                                     (2.16)

Схему “фильтрованного” звена второго порядка, соответствующего (2.16), можно получить, например, по схеме общего вид на рис. 2.2б. Такая схема показана на рис. 2.6а. На рис. 2.6б приведена эквивалентная схема, которая получается из первой, если поменять местами рекурсивную и нерекурсивную части цепи.

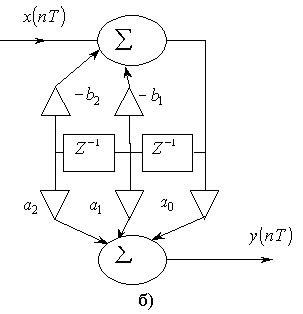
Рис. 2.6

Схемы фильтровых звеньев первого порядка получается из схемы фильтровых звеньев второго порядка как частный случай.

Примеры простейших функций первого порядка

, , , ,

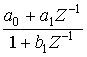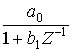Расчет ЦФ целесообразно проводить с применением нормирования  по частоте. Находит применение, например, нормирования к частоте , то есть

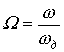                                                                                                   (2.17)

Подобно аналоговым фильтрам широко применяется логарифмический масштаб АЧХ

, дБ.                                                                              (2.18)

На выбор величины тактовой частоты  дополнительное ограничение оказывают следующие 2 фактора: снижение  ужесточает требования к восстанавливающему фильтру в ЦАП, повышение  ужесточает требования к быстродействию арифметических узлов ЦФ.