|
Электромагнитные поля и волны |
|
Лабораторная работа 1 |
ЦЕЛЬ РАБОТЫ: Исследование влияния параметров реальных сред на процесс распространения электромагнитных волн.
ЗАДАНИЕ ДЛЯ ПРЕДВАРИТЕЛЬНОГО РАСЧЕТА.
Для прямоугольного волновода сечением a![]() b мм, заполненного различными средами (см. таблицу 2), рассчитать для заданных в таблице 1 вариантов частоты f : коэффициент затухания α, фазовую постоянную β, модуль характеристического сопротивления
b мм, заполненного различными средами (см. таблицу 2), рассчитать для заданных в таблице 1 вариантов частоты f : коэффициент затухания α, фазовую постоянную β, модуль характеристического сопротивления
![]() , длину волны
, длину волны ![]() и фазовую скорость
и фазовую скорость ![]() в прямоугольном волноводе, заполненного средой. Определить эквивалентную проводимость среды
в прямоугольном волноводе, заполненного средой. Определить эквивалентную проводимость среды
![]() . В качестве исследуемых сред используются немагнитные среды. Относительная магнитная проницаемость m
для немагнитных сред всегда равна единице
. В качестве исследуемых сред используются немагнитные среды. Относительная магнитная проницаемость m
для немагнитных сред всегда равна единице ![]()
![]() .
.
Таблица 1
|
последняя цифра пароля |
1 |
2 |
3 |
4 |
||||||||
|
Вариант |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
|
Частота, ГГц |
7,5 |
10 |
8,15 |
7,6 |
9,8 |
8,25 |
7,7 |
9,6 |
8,35 |
7,8 |
9,4 |
8,45 |
|
последняя цифра пароля |
5 |
6 |
7 |
8 |
||||||||
|
Вариант |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
|
Частота, ГГц |
7,9 |
9,2 |
8,55 |
8,0 |
9,0 |
7,05 |
8,1 |
9,1 |
9,95 |
8,3 |
9,3 |
7,55 |
|
последняя цифра пароля |
9 |
10 |
11 |
12 |
||||||||
|
Вариант |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
|
Частота, ГГц |
8,5 |
9,5 |
7,65 |
8,7 |
9,7 |
7,75 |
8,9 |
9,9 |
7,85 |
8,2 |
8,8 |
9,85 |
Таблица 2
|
№ варианта |
Среда |
|
|
|
|
1 |
Фторопласт |
|
|
|
|
Текстолит |
|
|
|
|
|
2 |
Оргстекло |
|
|
|
|
Дерево |
|
|
|
|
|
3 |
Текстолит |
|
|
|
|
Дерево |
|
|
|
№ варианта выбирается самостоятельно.
Примечание: при проведении расчетов:
![]() ;
; ![]() ; а =23 мм; в = 10 мм.
; а =23 мм; в = 10 мм.
ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ.
Лабораторная установка (см. рис.1) состоит из генераторов сигнала СВЧ (1), измерительной линии (2), заполненной исследуемой средой (3), измерителя напряжения (4), короткозамыкателя (5) и согласованной поглощающей нагрузки (6).
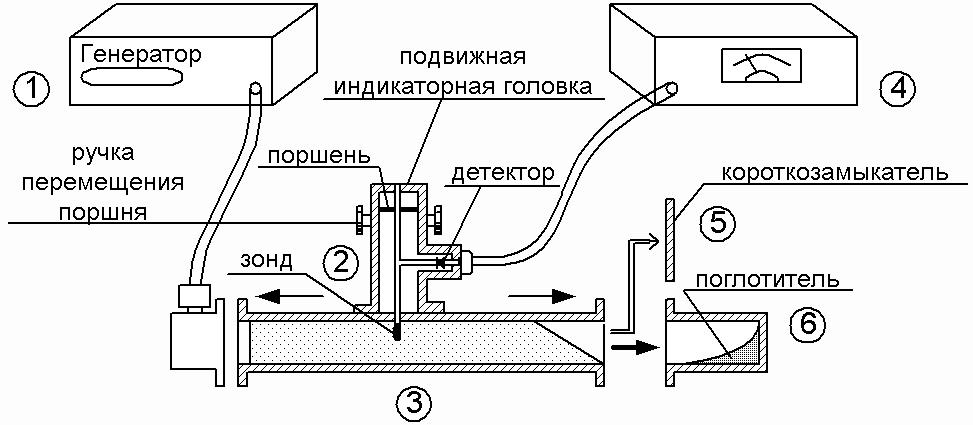
Рисунок 1 – Лабораторная установка
ЗАДАНИЕ И ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ.
ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ должен содержать:
1.Цель работы.
2.Блок-схема лабораторной установки.
3. Результаты предварительного расчета, представленные в виде
таблиц и графиков зависимости напряженности электрического поля от координаты z для различных сред.
4. Выводы по работе.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Под волновым процессом понимают возмущение некоторой величины в пространстве, перемещающееся с конечной скоростью и переносящее энергию без переноса вещества.
Математически волновой процесс описывается однородным уравнением Гельмгольца:
![]() ,
(1)
,
(1)
где 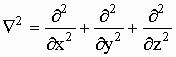 - оператор Лапласа,
- оператор Лапласа,
![]() - волновое число или постоянная распространения,
- волновое число или постоянная распространения,
![]() - абсолютные диэлектрическая и магнитная проницаемости,
- абсолютные диэлектрическая и магнитная проницаемости,
![]() -
относительные диэлектрическая и магнитная проницаемости.
-
относительные диэлектрическая и магнитная проницаемости.
Плоская электромагнитная волна
– это волновой процесс, у которого электрическая и магнитная составляющие
поля во всех точках плоскости, перпендикулярной направлению распространения
волны, имеют одинаковые значения. Если принять в качестве направления распространения
плоской электромагнитной волны ось z в декартовой системе координат, то, согласно
определению, поле плоской электромагнитной волны не зависит от поперечных
координат x и y. Следовательно,  и уравнение (1) принимает следующий вид:
и уравнение (1) принимает следующий вид:
 .
.
Решение данного дифференциального уравнения 2-го порядка имеет вид:
![]() ,
(2)
,
(2)
где ![]() – единичный вектор.
– единичный вектор.
Общее решение представляет собой два волновых процесса, распространяющихся на встречу друг друга, вдоль отрицательного и положительного направления оси z (волна падающая и отраженная). Поскольку в рассматриваемой задаче рассматривается один источник, то учитываем только волну с амплитудой А
![]() .
(3)
.
(3)
Выделим из комплексного выражения действительную часть:
![]() .
.
а) Плоская электромагнитная волна в идеальной среде.
Идеальной средой принято называть среду в которой отсутствуют потери энергии при распространении электромагнитной волны. Общая запись плоской электромагнитной волны в идеальной среде:
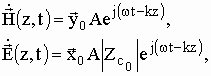 (4)
(4)
где k – вещественное волновое число.
Вектор напряженности магнитного поля перпендикулярен
вектору напряженности электрического поля. Электрическое и магнитное поля
колеблются в пространстве синхронно и синфазно. Коэффициент пропорциональности,
определяемый как ![]() , называется
характеристическим (волновым) сопротивлением данной среды
, называется
характеристическим (волновым) сопротивлением данной среды ![]() :
:
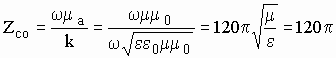 .
(5)
.
(5)
Из (5) видно, что ![]() полностью определяется лишь параметрами самой среды.
полностью определяется лишь параметрами самой среды.
Перейдем от комплексных значений в (4) к мгновенным, в результате получим:
 (6)
(6)
где ![]() - фаза колебаний.
- фаза колебаний.
Длина волны ![]() - это расстояние, которое проходит фазовый фронт за один период колебаний
высокой частоты. Отсюда фазовая скорость плоской электромагнитной волны в
идеальной среде равна:
- это расстояние, которое проходит фазовый фронт за один период колебаний
высокой частоты. Отсюда фазовая скорость плоской электромагнитной волны в
идеальной среде равна:
![]()
 ,
,
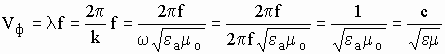 ,
(7)
,
(7)
где: 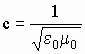 - скорость света.
- скорость света.
б) Плоская электромагнитная волна в реальной среде.
При распространении электромагнитных волн в реальных средах происходит частичное рассеивание их энергии, которое обусловлено потерями в среде. Различают два вида потерь в среде:
![]() ,
,
где ![]() .
.
При фиксированной частоте эти два вида потерь с макроскопической точки зрения неразличимы: как те так и другие потери приводят к преобразованию электромагнитной энергии в другие виды энергий. Вследствие этого комплексная диэлектрическая проницаемость среды с учетом обеих видов потерь запишется как:
![]() .
.
Можно формально ввести понятие эквивалентной
проводимости среды, соответствующую поляризационным потерям как: ![]() .
.
Отсюда: ![]() .
.
Тогда окончательно получаем:
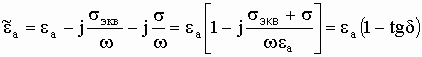 .
(8)
.
(8)
Отношение  - носит название тангенса угла потерь.
- носит название тангенса угла потерь.
Отношение 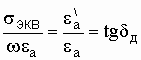 - носит название тангенса угла диэлектри-ческих
потерь.
- носит название тангенса угла диэлектри-ческих
потерь.
Разделение сред на диэлектрические и проводящие с физической точки зрения связанно с наличием свободных носителей заряда. В то же время можно сказать, что разделение сред на диэлектрики и проводники достаточно условно, поскольку одна и та же среда может вести себя по разному на различных частотах (например, морская вода на НЧ является проводником, а на СВЧ – диэлектриком).
В данной лабораторной работе исследуются
диэлектрические среды, для которых справедливо неравенство 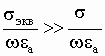 ,
поэтому:
,
поэтому:
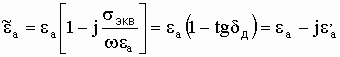 .
(9)
.
(9)
Вследствие этого, волновое число также является комплексной величиной:
![]() .
(10)
.
(10)
Вещественную часть волнового числа b называют фазовой постоянной, а мнимую часть a - коэффициентом затухания. Значения b и a можно найти непосредственно из (10):
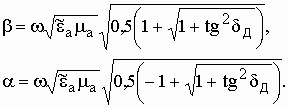 (11)
(11)
Таким образом, с учетом выражений (4) и (10) уравнение плоской электромагнитной волны в реальной безграничной среде запишется как:
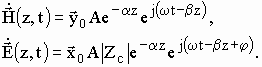
Перейдем к мгновенным значениям ![]() и
и ![]() , в результате получим:
, в результате получим:
 (12)
(12)
где 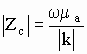 - модуль характеристического сопротивления реальной среды,
- модуль характеристического сопротивления реальной среды,
![]() - сдвиг по фазе.
- сдвиг по фазе.
Сравнивая уравнения (6) и (12), можно выявить следующие различая между плоской электромагнитной волной в идеальной и реальной среде:
а) Векторы Е и Н сдвинуты по фазе на угол, равный j ;
б) Множитель ![]() указывает на экспоненциальное ослабление поля в направлении распространения
волны, что связанно с преобразованием части электромагнитной энергии в другие
виды энергий. Отсюда очевиден физический смысл коэффициента затухания: a
характеризует уменьшение амплитуды волны на единицу длины.
указывает на экспоненциальное ослабление поля в направлении распространения
волны, что связанно с преобразованием части электромагнитной энергии в другие
виды энергий. Отсюда очевиден физический смысл коэффициента затухания: a
характеризует уменьшение амплитуды волны на единицу длины.
в) Роль волнового числа (постоянной распространения) электромагнитной волны в постоянной среде играет вещественная часть b комплексного волнового числа. Постоянная распространения b характеризует изменение фазы волны на единицу длины. По аналогии с идеальной средой, для реальной среды длина волны и фазовая скорость будут определяться как:
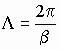 ,
,
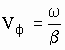 . (13)
. (13)
В заключении изобразим мгновенную картину плоской электромагнитной волны, распространяющейся в идеальной среде (рис. 2 а) и в реальной среде (рис. 2б).
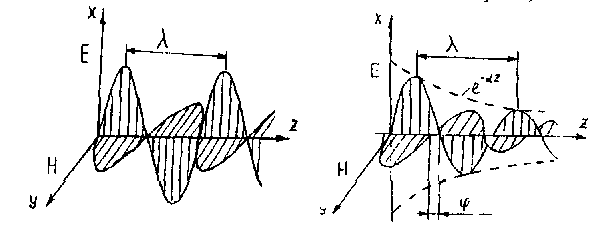
а) б)
Рисунок 2 – Эскиз взаимного расположения электрических и магнитных полей в пространстве а) в идеальных средах б) в реальных средах
в) Плоская электромагнитная волна в направляющей системе.
Для исследования поведения плоских электромагнитных волн в реальной среде в данной лабораторной работе используется направляющая система, позволяющая сосредоточить электромагнитную энергию в определенном пространстве и передать ее в заданном направлении. Примером направляющей системы может, в частности, служить полая металлическая труба прямоугольного сечения, носящая название прямоугольный волновод. Электромагнитное поле в прямоугольном волноводе можно рассматривать как результат сложения плоских электромагнитных волн, рассмотренных ранее, многократно отраженных под углом g от граничных поверхностей, образующих волновод (см. рис. 3).
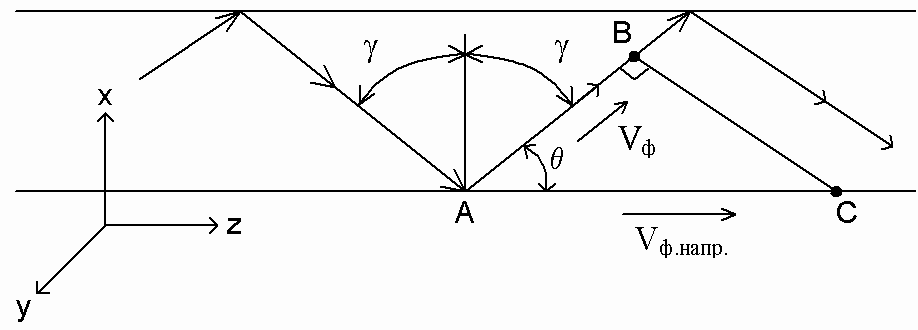
Рисунок 3 – Электромагнитное поле в прямоугольном волноводе
Плоская электромагнитная волна, двигаясь
от точки А до точки В, за время ![]() пройдет расстояние АВ равное
пройдет расстояние АВ равное ![]() .
За это же время волна вдоль стенки волновода пройдет расстояние
.
За это же время волна вдоль стенки волновода пройдет расстояние ![]() и равное
и равное ![]() . Таким образом:
. Таким образом: 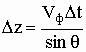 ,
фазовая скорость электромагнитной волны в направляющей системе:
,
фазовая скорость электромагнитной волны в направляющей системе:
 .
.
Так как ![]() ,
то отличительной особенностью направляющих систем является то, что фазовая
скорость распространения электромагнитной волны в них больше чем фазовая скорость
волны в неограниченной среде. В частности для прямоугольного волновода:
,
то отличительной особенностью направляющих систем является то, что фазовая
скорость распространения электромагнитной волны в них больше чем фазовая скорость
волны в неограниченной среде. В частности для прямоугольного волновода:
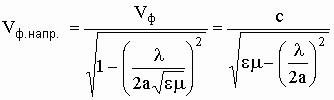 ,
(14)
,
(14)
где: ![]() - длина волны в свободном пространстве;
- длина волны в свободном пространстве;
а – размер широкой стенки прямоугольного волновода.
Исходя из (13) и (14) нетрудно определить основные параметры электромагнитной волны в прямоугольном волноводе, заполнено реальной средой:
Постоянная распространения волны в прямоугольном волноводе b :
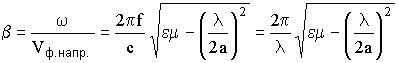 ,
,
 . (15)
. (15)
Длина волны в прямоугольном волноводе
![]() :
:
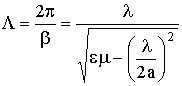 ,
,
![]() . (16)
. (16)
Модуль характеристического сопротивления прямоугольного волновода:
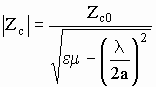 .
(17)
.
(17)
Коэффициент затухания a в прямоугольном волноводе:
 ,
,
![]() . (18)
. (18)
На практике, чтобы определить затухание
волны ![]() в прямоугольном волноводе
при прохождении пути L, берут отношение амплитуд на концах этого участка:
в прямоугольном волноводе
при прохождении пути L, берут отношение амплитуд на концах этого участка:
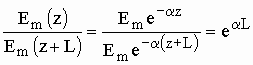 .
.
Затухание в децибелах определяют как двадцать десятичных логарифмов от этого отношения:
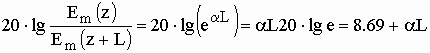 .
.
Отсюда:
 ,
,
![]() . (19)
. (19)
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какая волна называется плоской волной? При каком условии электромагнитную волну можно считать плоской волной?
2. Какие среды называют идеальными, какие реальными? Приведите примеры идеальных и реальных сред.
3. Чем обусловлены потери энергии электромагнитной волны в диэлектрике, проводнике и вакууме?
4. Поясните физический смысл коэффициента затухания и фазовой постоянной.
5. Что называют длиной волны и периодом колебаний?
6. Записать уравнение плоской волны для электрического и магнитного полей в идеальной среде.
7. Записать уравнение плоской волны для электрического и магнитного полей в реальной среде.
8. Поясните физический смысл тангенса угла потерь.
9. Какое физическое явление используется для измерения диэлектрической проницаемости?
10. Какое физическое явление используется для измерения коэффициента затухания?
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Вольман В.И., Пименов Ю.В. Техническая электродинамика:
Учебник для вузов. М.: Связь, 1971, стр. 166-230.
2. Семенов Н.А. Техническая электродинамика: Учебник для вузов.
М.: Связь, 1973, стр. 98-117.