|
Электромагнитные поля и волны |
|
Лабораторная работа 3 |
|
Цель работы:
1. Исследование дисперсионных характеристик прямоугольного волновода: зависимости длины волны в волноводе и фазовой скорости в волноводе от частоты.
2. Исследование распределения электромагнитного поля в поперечном сечении прямоугольного волновода на примере волны Н10.
1 Задание для предварительного расчета
Исходные данные для предварительного расчета в таблице 1.
Таблица 1.
|
M |
N |
а, мм |
Частоты генератора, ГГц |
||||
|
1 |
1 2 3 |
28.5 28.5 28.5 |
5.60 5.65 5.75 |
5.90 5.95 6.05 |
6.20 6.25 6.35 |
6.50 6.55 6.65 |
6.80 6.85 6.95 |
|
2 |
4 5 6 |
28.5 28.5 28.5 |
5.70 5.85 5.87 |
6.00 6.15 6.17 |
6.30 6.45 6.47 |
6.60 6.75 6.77 |
6.90 7.05 7.07 |
|
3 |
7 8 9 |
28.5 28.5 28.5 |
5.80 5.95 5.97 |
6.10 6.25 6.27 |
6.40 6.55 6.57 |
6.70 6.85 6.87 |
7.00 7.15 7.17 |
|
4 |
10 11 12 |
28.5 28.5 28.5 |
5.90 6.05 6.09 |
6.20 6.35 6.39 |
6.50 6.65 6.69 |
6.80 6.95 6.99 |
7.10 7.25 7.29 |
|
5 |
13 14 15 |
28.5 28.5 28.5 |
6.00 6.15 6.19 |
6.30 6.45 6.49 |
6.60 6.75 6.79 |
6.90 7.05 7.09 |
7.20 7.35 7.39 |
|
6 |
16 17 18 |
28.5 28.5 28.5 |
6.10 6.20 6.25 |
6.40 6.50 6.55 |
6.70 6.80 6.85 |
7.00 7.10 7.15 |
7.30 7.40 7.45 |
|
7 |
19 20 21 |
23.0 23.0 23.0 |
8.00 8.15 8.25 |
8.40 8.55 8.05 |
8.80 8.95 9.05 |
9.20 9.35 9.45 |
9.60 9.75 9.85 |
|
8 |
22 23 24 |
23.0 23.0 23.0 |
8.10 8.29 8.35 |
8.50 8.69 8.75 |
8.90 9.09 9.15 |
9.30 9.49 9.55 |
9.70 9.89 9.95 |
|
9 |
25 26 27 |
23.0 23.0 23.0 |
8.20 8.37 8.45 |
8.60 8.77 8.85 |
9.00 9.17 9.25 |
9.40 9.57 9.65 |
9.80 9.97 10.05 |
|
10 |
28 29 30 |
23.0 23.0 23.0 |
8.30 8.47 8.55 |
8.70 8.87 8.95 |
9.10 9.27 9.35 |
9.50 9.67 9.75 |
9.90 10.07 10.15 |
|
11 |
31 32 33 |
23.0 23.0 23.0 |
8.40 8.57 8.65 |
8.80 8.97 9.05 |
9.20 9.37 9.45 |
9.60 9.77 9.85 |
10.00 10.17 10.25 |
|
12 |
34 35 36 |
23.0 23.0 23.0 |
8.50 8.67 8.75 |
8.90 9.07 9.15 |
9.30 9.47 9.55 |
9.70 9.87 9.95 |
10.10 10.27 10.35 |
М – последняя цифра пароля, N – две последние цифры пароля.
2 ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ
Лабораторная установка (рисунок 1) состоит из генератора СВЧ сигналов1, волноводной измерительной линии 2, устройства для измерения поля в поперечном сечении 3, короткозамкнутой нагрузки 4, согласующей нагрузки 5, индикаторного прибора 6.
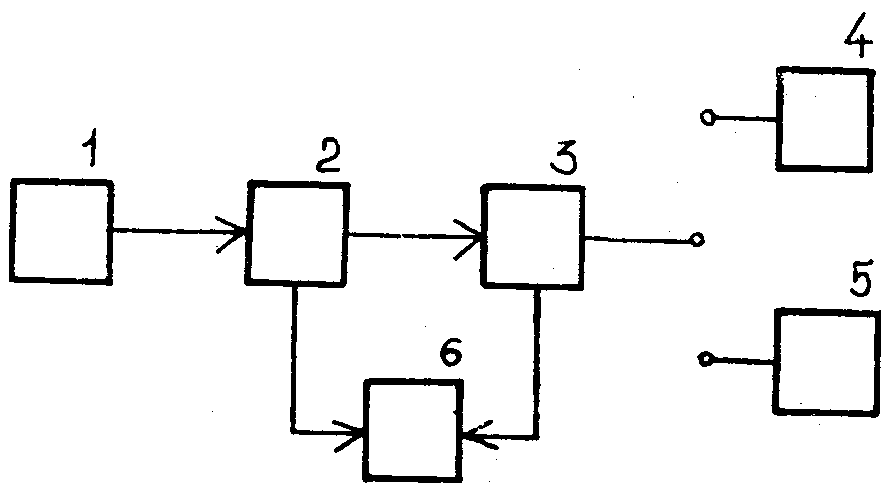
Рисунок 1 - Структурная схема лабораторной установки
Измерительная линия 2 с устройством 3 позволяет осуществить перемещение зонда вдоль и поперек волновода, с целью получения зависимости напряженности поля в волноводе от координат х и z. Для того, чтобы получить зависимость амплитуды напряженности поля от координаты х необходимо извлечь корень квадратный из показаний индикатора, так как в исследуемой цепи включены детекторы, вольтамперную характеристику которых при небольших уровнях сигнала можно считать квадратичной, поэтому индикаторы фиксируют показания пропорциональные мощности сигнала. Величина пропорциональная напряженности поля измеряется в относительных единицах. За единицу принимаются максимальные показания индикатора.
3 КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Направляющие системы
Электромагнитные волны, направляемые регулярными линиями передачи
Линии передачи и их классификации
Устройства, ограничивающие область, в которой распространяются электромагнитные волны, и направляющие поток электромагнитной энергии в заданном направлении ( например, от передатчика к антенне), называют линиями передачи.
Регулярные линии передачи – это линии, электродинамические и геометрические свойства которых в любом поперечном сечении линии постоянны.
Основные типы регулярных линий передачи (рисунок 1) можно разделить на две группы – открытые линии (многосвязные системы ) и волноводы (односвязные системы). Поперечные сечения открытой линии не имеет замкнутого проводящего ( металлического ) контура, охватывающего снаружи область распространения электромагнитной энергии. Поэтому в открытых линиях передачи поле направляемой волны не экранировано снаружи и существует в пространстве, окружающем линию. Основными типами этих линий являются: симметричная двухпроводная линия, выполненная из круглых проводов (рисунок 1а), полосковая линия, состоящая из металлических полосок, разделенных диэлектриком (рисунок 1б), диэлектрическая линия, представляющая собой стержень из диэлектрика (рисунок 1в) и т.д.
Поперечное сечение закрытых линий имеет замкнутый проводящий контур, охватывающий снаружи область распространения электромагнитной энергии. Основными типами закрытых линий являются волноводы: прямоугольный (рисунок 1г), круглый (рисунок 1д), П-образный (рисунок 1е), эллиптический (рисунок 1ж) и коаксиальный кабель (рисунок 1з).
Симметричные двухпроводные линии целесообразно применять на метровых и более длинных волнах, коаксиальные линии на дециметровых и более длинных волнах, прямоугольный, круглый и эллиптический волноводы – на сантиметровых и миллиметровых волнах, диэлектрическую линию – на миллиметровых и более коротких волнах
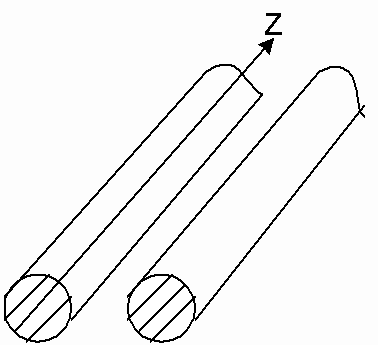

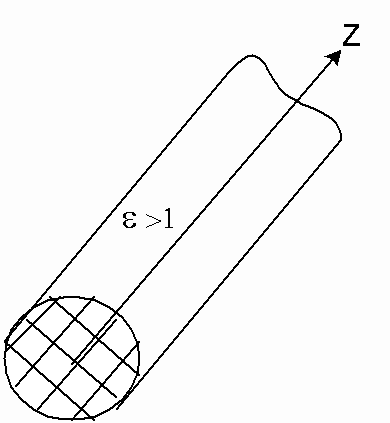
а) б) в)
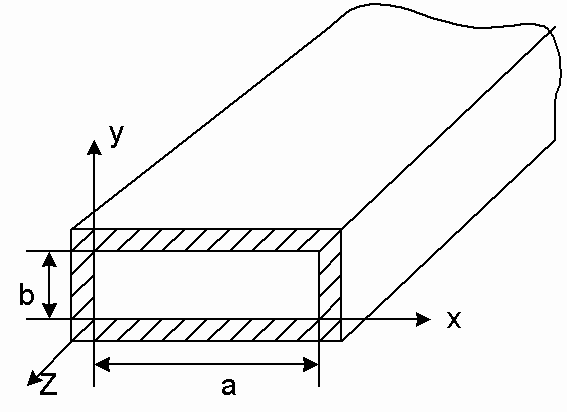
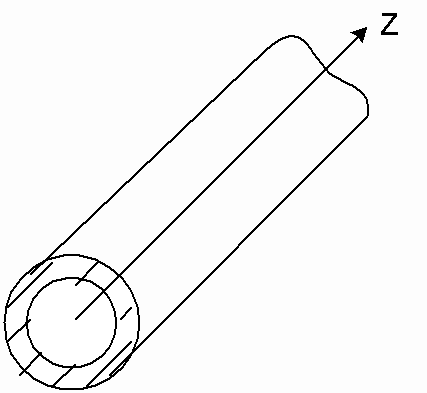
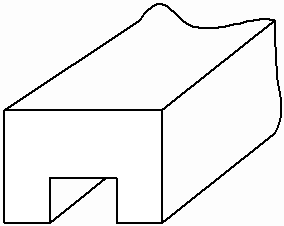
г) д) е)
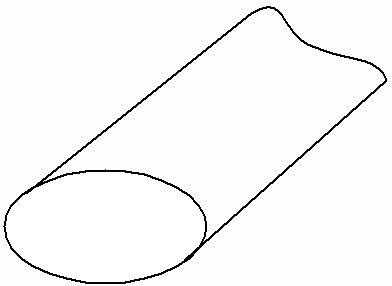
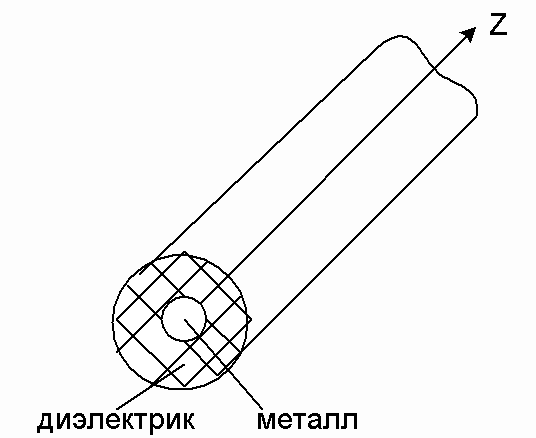
ж) з)
Рисунок 1 – Основные типы линий передачи
Недостатки двухпроводных и коаксиальных линий передачи :
В двухпроводных и коаксиальных линиях резко возрастают потери энергии с ростом частоты. Основные факторы потерь энергии:
Некоторые примеры:
В двухпроводных линиях при l = 1м и короче потери такие большие, что их нецелесообразно применять.
В коаксиальном кабеле на l = 3м затухание в среднем 0.2 дБ/м, а на
l = 10 см затухание 2 дБ/м .
Достоинства волноводов:
Особенности направляемых электромагнитных волн
В любой направляющей системе, ориентированной вдоль оси Z, распространяются разные типы (моды) плоских электромагнитных волн, отличающиеся друг от друга продольным волновым числом g .
![]() (1)
(1)
где : F (x,y.z) любая компонента напряженности электромагнитного поля (Ex, Ey, Ez, Hx, Hy, Hz)
g - продольное волновое число
![]() (2)
(2)
ks – поперечное волновое число, разное для различных типов волн.
k – волновое число в свободном пространстве
![]() , l
- длина волны генератора.
, l
- длина волны генератора.
ks – называют критическим волновым числом, потому что при k < ks g становится чисто мнимым числом, поэтому волна в волноводе отсутствует. Помимо критического волнового числа вводят понятия критической длины волны l кр и критической частоты fкр по определению
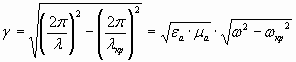
![]() (3)
(3)
где ![]()
Каждый тип волны имеет свое критическое волновое число ks, свою критическую длину волны l кр и свою критическую частоту fкр .
Из приведенных формул следует, что фазовая скорость Vф=![]() всегда больше скорости света С , а групповая скорость
всегда больше скорости света С , а групповая скорость ![]() всегда меньше скорости света С . Нетрудно показать, что произведение
всегда меньше скорости света С . Нетрудно показать, что произведение
![]() .
.
В произвольных направляющих системах различают 4 класса волн (мод).
1-й класс – Электрические волны Еz ≠ 0, Нz = 0 (Е-волны)
2-й класс – Магнитные волны Нz ≠ 0, Еz = 0 (Н-волны)
3-й класс – Поперечные волны Нz = 0, Еz = 0 (Т-волны) плоская ЭМВ
4-й класс – Гибридные волны Еz ≠ 0, Нz ≠ 0 ( характерны для световодов)
Классификация волн позволяет упростить анализ волн в волноводах и записать все составляющие полей через одну продольную составляющую
{ Ех , Еу , Нх , Ну} = f (Еz , Нz )
Любая электромагнитная волна в волноводе может быть представлена в виде линейной комбинации этих типов волн. В волноводах могут существовать только моды Е и Н, в открытых системах и коаксиальном кабеле могут существовать 1,2,3 классы. В диэлектрических направляющих системах, как правило, существуют гибридные волны.
Прямоугольный волновод
Прямоугольный волновод представляет собой полую металлическую трубу прямоугольного сечения (рисунок 2).
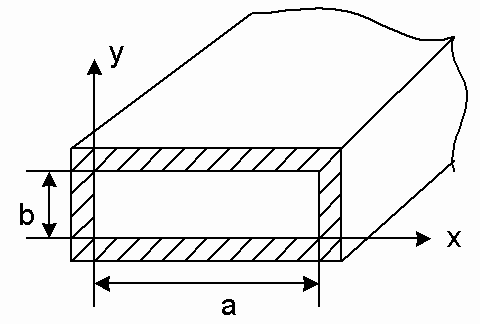
Рисунок 2 – Прямоугольный волновод
Моды ЭМВ обозначают с помощью двух индексов m и n . В случае электрических волн (Emn), в случае магнитных волн (Hmn).
Е – волны в прямоугольном волноводе ( Еz ≠ 0, Нz = 0)
Решая граничные задачи в прямоугольном волноводе для волн типа Еmn , с граничным условием равенства нулю касательной составляющей на поверхности волновода Еt = 0 имеем :
![]()
![]()
![]()
![]() (4)
(4)
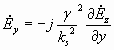
![]()
где : m – число полуволн вдоль оси х
n – число полуволн вдоль оси y
![]() - характеристическое сопротивление в случае Е-волн
- характеристическое сопротивление в случае Е-волн
![]()
Если m = 0 и n = 0, то Ez = 0 - поля в волноводе нет . Основная волна Е11 .
Н – волны в прямоугольном волноводе (Нz ≠ 0, Еz = 0)
Решая граничные задачи в прямоугольном волноводе для волн типа Нmn , с граничным условием равенства нулю касательной составляющей на поверхности волновода Еt = 0 имеем :
![]()
![]()
![]()
![]() (5)
(5)
![]()
![]()
![]() - характеристическое сопротивление в случае Н-волн
- характеристическое сопротивление в случае Н-волн
![]() - продольное волновое число
- продольное волновое число
![]() - поперечное волновое число
- поперечное волновое число
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, 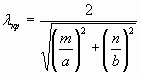 ,
, ![]() (6)
(6)
![]() - волновое число в свободном пространстве
- волновое число в свободном пространстве
В случае Н-волн в прямоугольном волноводе индексы m и n одновременно не могут быть равны 0 . Минимальные значения индексов m и n в случае Нmn
m = 1, n = 0 . Основная волна в прямоугольном волноводе Н10 .
Основная волна в прямоугольном волноводе
Преимущества волны Н10
Составляющие волны Н10 получаем из (5), полагая m = 1 , n = 0.
![]()
![]() (7)
(7)
![]()
![]()
![]()
![]()
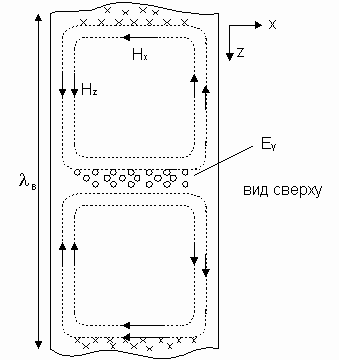
Восстановим из уравнений (7) распределение силовых линий Е и Н для волны Н10 (рисунок 3). Рассмотрим поперечное сечение волновода.
Электрическое поле Е направлено от одной стенки к другой. А магнитное поле Н (вид сверху) имеет две составляющие Нх и Нz . У боковых стенок волновода Нz максимально и изменяется по закону cos. В силу непрерывности линий магнитного поля Н замыкается через Нх (Нz переходит в Нх). Эта картинка перемещается в волноводе с фазовой скоростью Vф, которая больше скорости света Vф > с .
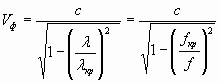 ,
, ![]()
Групповая скорость волны
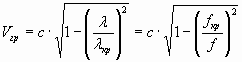 ,
, ![]()
Характеристическое сопротивление волны
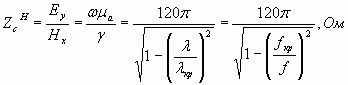 (8)
(8)
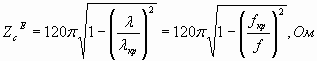
Фазовая скорость Vф зависит от частоты. Зависимость фазовой скорости от частоты называется дисперсией.
Структура поля волны Н10
Y EY
поперечное сечение
b Hx
Нх Нх
x
а
 .
.
Рисунок 3 – Структура поля волны Н10 в двух проекциях
Структура поля волны Н20
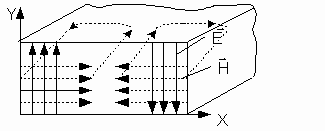
Рисунок 4 – Структура поля волны Н20
Токи в стенках волновода
Переменное магнитное поле в металлической стенке создает ток. Токи, протекающие в стенках волновода, надо знать по следующим причинам.
Плотность поверхностного тока численно равна касательной составляющей магнитного поля НZ и они взаимно перпендикулярны
![]() , или
, или ![]() (9)
(9)
Токи удобнее представлять на развертке волновода (рисунок 5).
Составляющая Нх порождает ток продольный IZ . В широкой стенке два тока: продольный IZ и поперечный Ix . Поперечный ток Ix порождает составляющая НZ . В узкой стенке волновода поперечный ток Iy , который порождает составляющая НZ . Для извлечения энергии из волновода на стенках волновода вырезают щели. Если щель пересекает токи, то она будет излучать, если щель параллельна токам, то она не излучает (рисунок 6).
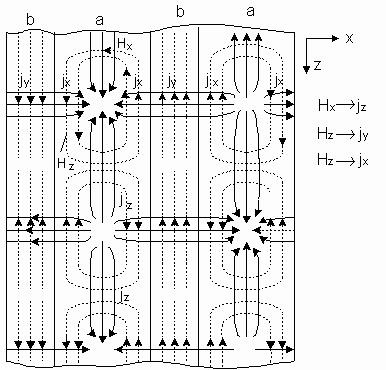
Рисунок 5 – Токи в стенках волновода
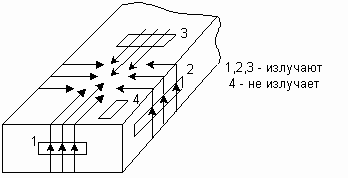
Рисунок 6 – Извлечение энергии из волновода
Передача энергии по волноводу
Процесс передачи энергии по волноводу рассмотрим на примере основной волны Н10
![]() ,
, ![]() - сопряженная величина
- сопряженная величина
i j k
![]() Ex Ey Ez
Ex Ey Ez ![]() (10)
(10)
Hx Hy Hz
![]()
Для волны Н10 Ех = 0, Нy =0 . Из (11) следует, что энергия, передаваемая по волноводу, определяется только поперечными составляющими полей

Отсюда средняя мощность, передаваемая по волноводу
![]()
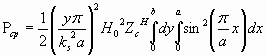
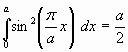 - табличный интеграл
- табличный интеграл
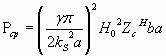 (11)
(11)
Эта величина только зависит от амплитуды продольной составляющей магнитного поля ![]() .
.
Составляющая Н0 численно равна поперечному току в стенках волновода
![]()
С увеличением размеров волновода передаваемая мощность возрастает.
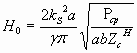 (12)
(12)
Напряженность электрического поля возрастает с ростом передаваемой по волноводу мощности.
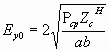
Если волновод заполнен воздухом, то Епроб max ![]() 30 кВ/см. Отсюда Еy0=Епроб max
30 кВ/см. Отсюда Еy0=Епроб max![]() 30 кВ/см =
30 кВ/см =
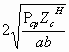 - для воздуха, откуда
- для воздуха, откуда
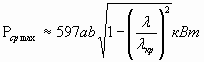 , где а, b в см (14)
, где а, b в см (14)
Для стандартного волновода R 100 a = 2,3 см, b = 1,0 см Рср max ![]() 1 мВт
1 мВт
При проектировании волноводов и различных СВЧ устройств делают запас прочности Рраб = (0.2¸ 0.3) Рср max . Один из путей повышения уровня передаваемой мощности связан с заполнением его средой, имеющей более высокое значение пробивного напряжения.
Потери энергии в волноводе
Можно выделить три основных фактора, которые приводят к потерям энергии в волноводе:
Основной из перечисленных причин являются джоулевые потери. Указанные выше факторы приводят к тому, что постоянная распространения будет величиной комплексной
![]()
Оценим потери на отрезке волновода длиной равной 1 м (рисунок 7).
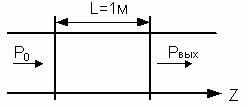
Рисунок 7 – Потери энергии в волноводе
Р0 – мощность на входе
Рвых – мощность на выходе
Рпотерь – мощность потерь
Рпотерь = Р0 – Рвых
Если на входе Е0 , то на выходе Евых = Е0× е-a z
На входе Н0 на выходе Нвых = Н0× е-a z
![]()
![]()
Для сред, когда a < < 1, тогда
![]() (разложение в ряд) (15)
(разложение в ряд) (15)
![]()
![]()
Для расчета потерь используют соотношение
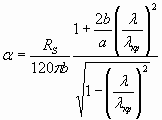 ,
, ![]() (16)
(16)
![]()
Rs – поверхностное сопротивление
![]() - удельная проводимость
- удельная проводимость
![]() - абсолютная магнитная проницаемость
- абсолютная магнитная проницаемость
Соотношение (17) дает не точный ответ, т.к. оно не учитывает качество обработки внутренней поверхности волновода. Чем качественнее механическая обработка, тем меньше потери. Для уменьшения потерь необходимо :
Таблица 2
Результаты расчета электрического
поля в поперечном сечении волновода
|
Теоретический расчет |
|
|
Х, мм |
|
|
0 3 6 9 11.5 12 14.25 15 18 21 23 25 28.5 |
|
Таблица 3
Результаты расчета и l в, Vф
|
Теоретический расчет |
||
|
f |
λв (f) |
Vф (f) |
|
|
||
Примечание:
5 Содержание отчета должно включать:
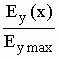 , λв = F (f), Vф = F (f).
, λв = F (f), Vф = F (f).
6 Контрольные вопросы
7 Литература