|
Электромагнитные поля и волны |
|
Лабораторная работа 4 |
ЛАБОРАТОРНАЯ РАБОТА
ИССЛЕДОВАНИЕ СВЧ ОБЪЕМНЫХ РЕЗОНАТОРОВ
Для заданных в таблице вариантов* резонансной частоты f0 и полосы пропускания Δf провести конструктивный расчет прямоугольного резонатора с колебанием Н101, Рис.1:
|
М |
а х в, мм |
Вариант 1 |
М |
а х в, мм |
Вариант 2 |
||
|
f0, ГГц |
Δf, МГц |
f0, ГГц |
Δf, МГц |
||||
|
1 |
23,0 х 10,0 |
10,24 |
55,0 |
13 |
23,0 х 10,0 |
9,67 |
36,0 |
|
2 |
28,5 х 12,6 |
7,68 |
60,0 |
14 |
28,5 х 12,6 |
7,27 |
43,0 |
|
3 |
58,0 х 25,0 |
4,05 |
32,0 |
15 |
58,0 х 25,0 |
3,80 |
23,0 |
|
4 |
23,0 х 10,0 |
9,56 |
75,0 |
16 |
23,0 х 10,0 |
9,13 |
56,0 |
|
5 |
28,5 х 12,6 |
7,24 |
55,0 |
17 |
28,5 х 12,6 |
7,03 |
45,0 |
|
6 |
58,0 х 25,0 |
3,79 |
38,0 |
18 |
58,0 х 25,0 |
3,62 |
28,0 |
|
7 |
23,0 х 10,0 |
9,02 |
101,0 |
19 |
23,0 х 10,0 |
9,93 |
190,0 |
|
8 |
28,5 х 12,6 |
7,00 |
56,0 |
20 |
28,5 х 12,6 |
7,59 |
100,0 |
|
9 |
58,0 х 25,0 |
3,58 |
45,0 |
21 |
58,0 х 25,0 |
3,94 |
84,0 |
|
10 |
23,0 х 10,0 |
9,75 |
310,0 |
22 |
23,0 х 10,0 |
9,27 |
225,0 |
|
11 |
28,5 х 12,6 |
7,55 |
120,0 |
23 |
28,5 х 12,6 |
7,17 |
88,0 |
|
12 |
58,0 х 25,0 |
3,88 |
125,0 |
24 |
58,0 х 25,0 |
3,69 |
90,0 |
М – две последние цифры пароля
Объемные резонаторы используют в качестве резонансных звеньев полоснопропускающих и полоснозагрождающих СВЧ фильтров, для стабилизации частоты СВЧ – генераторов. Перестраиваемые объемные резонаторы широко применяются при СВЧ – измерениях.
В большинстве случаев объемный резонатор представляет собой отрезок направляющей системы СВЧ, ограниченный с двух сторон проводящей поверхностью. По типу используемой направляющей системы можно выделить прямоугольные, цилиндрические, коаксиальные объемные резонаторы.
При исследовании свойств объемных резонаторов следует различать два типа задач:
При решении задачи о собственных колебаниях рассматривают объемный резонатор, изолированный от генератора и нагрузки. Решение трехмерного волнового уравнения с граничными условиями, определяемыми формулой и размерами резонатора, позволяет определить типы и собственные частоты колебаний, которые могут существовать в исследуемом резонаторе, а также структуру Е и Н – составляющих поля в резонаторе. По известной структуре поля можно определить отношение энергии, запасенной в резонаторе к энергии, теряемой в резонаторе за период. Решение задачи о собственных колебаниях строго проводится только методами теории поля.
При решении задачи о вынужденных колебаниях рассматривают объемный резонатор, связанный с генератором и нагрузкой. Такая схема включения объемного резонатора обычно применяется на практике. Очевидно, что в этом случае разработчиков интересует резонансная частота резонатора на выбранном типе колебаний, потери на резонансной частоте, полоса пропускания объемного резонатора и учет влияния элементов связи на эти параметры. В большинстве случаев при расчетах для режима вынужденных колебаний анализ проводят методами теории цепей с использованием эквивалентных схем, созданных на основе данных, полученных из строгого решения задачи о собственных колебаниях.
При дальнейшем рассмотрении физических процессов, происходящих в объемных резонаторах, будем проводить аналогию с колебательными LC – контурами.
4.1. Режим собственных колебаний.
В режиме собственных колебаний объемный резонатор изолирован от генератора и нагрузки и представляет собой объем, ограниченный металлической поверхностью. Распределение электромагнитного поля в этом объеме должно удовлетворять граничным условиям, то есть касательная составляющая вектора напряженности электрического поля на поверхности проводника должна быть равна нулю. Решение уравнений Максвелла с учетом граничных условий показывает, что электромагнитное поле в таком объеме может существовать только на определенных частотах – собственных частотах резонатора.
Прямоугольный резонатор, Рис. 1а можно рассматривать как отрезок прямоугольного волновода с сечением а х в и длиной ℓ, закороченного с торцов. Граничным условиям на широкой и узкой стенках резонатора удовлетворяют поля волн Нmn и Еmn – типов прямоугольного волновода. Для удовлетворения граничным условиям на торцевых стенках для волн Н-типа необходимо, чтобы на длине резонатора ℓ укладывалось целое число полуволн, Рис.1б, в.
![]() , р – целое число
, р – целое число
Аналогичное условие выполняется и для цилиндрического резонатора, Рис. 1г.
Рис. 1
Тип колебаний определяется типом волны Нmn или Еmn в направляющей системе и числом полуволн, укладывающих на длине резонатора. Например, в прямоугольном резонаторе колебаний Нmnp имеет m – вариаций поля по оси Х, n – вариаций по оси У и р – вариаций по оси Z. На рис. 1б указано распределение составляющей Еу для колебаний Н101 и на рис. 1в для Н102.
Выражение для собственных частот объемных резонаторов легко получить, учитывая связь волнового числа ![]() с поперечными К^
и продольными
с поперечными К^
и продольными ![]() волновыми числами.
волновыми числами.
К2 = К2^ + g 2
Учитывая, что в резонаторе ![]() и переходя к частоте
и переходя к частоте 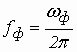 , получим
, получим
 , (4.1)
, (4.1)
где: с – скорость света,
e , m - относительная диэлектрическая и магнитная проницаемости среды внутри резонатора,
К^ - поперечное волновое число, определяемое формой поперечного сечения резонатора.
Для прямоугольного резонатора 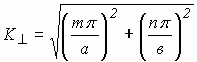 .
.
В случае круглого резонатора с радиусом R ![]() для волн Еnm и
для волн Еnm и ![]() для волн Нnm, где u
nm – m – корень функции Бесселя порядка n и m
nm – m – корень производной функции Бесселя порядка n.
для волн Нnm, где u
nm – m – корень функции Бесселя порядка n и m
nm – m – корень производной функции Бесселя порядка n.
Полученное выражение (4.1) позволяет сделать вывод, что в объемном резонаторе может существовать бесконечное множество собственных частот f0mnp в отличии от LC – контура, имеющего единственную собственную частоту
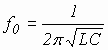 .
.
Следует отметить важные особенности:
На собственных резонансных частотах в объемном резонаторе происходит обмен энергией между электрическим и магнитным полями аналогично как в LC – колебательном контуре. На рис.2 показаны картины поля в объемном резонаторе в моменты времени w
t = 0, ![]() , p
, 3/2p
, когда поле является чисто электрическим, чисто магнитным и соответствующие им напряжения и токи в LC – контуре. Энергию электрического поля можно вычислить, интегрируя по объему квадрат модуля напряженности электрического поля
, p
, 3/2p
, когда поле является чисто электрическим, чисто магнитным и соответствующие им напряжения и токи в LC – контуре. Энергию электрического поля можно вычислить, интегрируя по объему квадрат модуля напряженности электрического поля
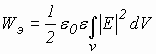 . (4.2)
. (4.2)
Энергия магнитного поля 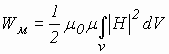 , причем Wм = Wэ.
, причем Wм = Wэ.
При отсутствии диссипативных потерь в идеальном объемном резонаторе процесс обмена энергией происходит с частотой f0mnpбесконечно долго.
В реальном объемном резонаторе, выполненном из металла с конечной проводимостью, всегда имеются диссипативные потери
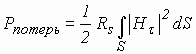 , (4.3)
, (4.3)
где: Нt - касательная к стенкам резонатора составляющая магнитного поля, определяющая плотность токов проводимости ê jsê = ê Ht ê на внутренней поверхности резонатора,
Rs – поверхностное сопротивление металлических стенок, определяемое проводимостью стенок s
, и частотой колебания, 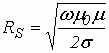 .
.
Для оценки качества резонатора вводится понятие собственной добротности
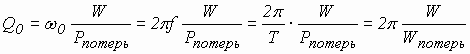 , (4.5)
, (4.5)
где: W – энергия, запасенная в резонаторе W = Wэ + Wм,
Рпотерь мощность потерь в резонаторе,
w 0 – собственная резонансная частота колебания,
Wпотерь – энергия тепловых потерь в резонаторе за период.
Для выяснения физического смысла собственной добротности Q0 воспользуемся теоремой Умова – Пойтинга. Уменьшение во времени энергии электромагнитного поля в замкнутом объеме может происходить только за счет диссипативных потерь внутри резонатора, так как излучение отсутствует
![]() (4.6)
(4.6)
Выражая Рпотерь из соотношения для собственной добротности, получим дифференциальное уравнение первого порядка
 , (4.7)
, (4.7)
решение которого 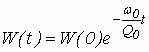 .
.
То есть энергия в объемном резонаторе уменьшается по экспоненте, при чем меньше Q0, тем быстрее уменьшается энергия, запасенная в резонаторе, Рис.3.
Рис. 3
Следует отметить, что энергетическое определение собственной добротности справедливо и для LC – колебательного контура. На рис. 4 показана эквивалентная схема объемного резонатора в режиме собственных колебаний, применение которой возможно лишь вблизи f0mnp, выбранного типа колебаний.
Величина собственной добротности объемного резонатора, как видно из приведенных соотношений, зависит от:
Собственные частоты
 ;
; 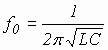
Собственная добротность
 ;
; 
Рис.4
а) не допускаются щели, т.к. в этом случае появляется излучение и Q0 резко уменьшается;
б) шлифовка и полировка внутренней поверхности резонатора приводит к увеличению Q0;
4.2. Режим вынужденных колебаний
В режиме вынужденных колебаний объемный резонатор связан с генератором и нагрузкой. Связь осуществляется обычно при помощи диафрагм связи, зондов или петель. Рис. 5.
Рис. 5
Так как резонатор обладает свойством запасать энергию на резонансной частоте f0, то к нагрузке мощность будет передаваться избирательно. Функция рабочего ослабления резонатора, Рис. 6
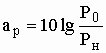 , дБ (4.8)
, дБ (4.8)
где Рн – мощность на выходе генератора, поступающая в нагрузку;
Р0 – мощность, отдаваемая генератором в согласованную нагрузку.
Полоса пропускания резонатора D
f определяется по уровню половинной мощности Рн = ![]() (ар = 10lg2 = 3 дБ), потери на резонансной частоте ар0 зависят от собственной Q0 и нагруженной добротности резонатора.
(ар = 10lg2 = 3 дБ), потери на резонансной частоте ар0 зависят от собственной Q0 и нагруженной добротности резонатора.
Нагруженную добротность можно определить по измеренной АЧХ
![]() , (4.9)
, (4.9)
и пользуясь энергетическим определением
 (4.10)
(4.10)
где: W – энергия, запасенная в резонаторе;
Рпотерь – мощность потерь в резонаторе;
Рг – мощность потерь на внутреннем сопротивлении генератора Rг;
Рн – мощность потерь в нагрузке Rн.
Для пояснения смысла Qн удобно ввести эквивалентную схему, которая вблизи резонанса на частоте f0mnp имеет аналогичную функцию рабочего ослабления, рис. 7.
Положим, что напряжение источника в некоторый момент времени скачком падает до нуля. Тогда энергия W, накопленная в резонаторе, расходуется на диссипативные потери в сопротивлениях Rг, Rн, R. Очевидно, что добротность нагруженного LC – контура
 всегда меньше собственной добротности
всегда меньше собственной добротности ![]() . В объемном резонаторе энергия, накопленная в резонаторе, точно также расходуется на диссипативные потери внутри резонаторе, часть энергии отводится через элементы связи и поглощается в нагрузке и на внутреннем сопротивлении генератора. Причем соотношение между величинами потерь внутри резонатора с генератором и нагрузкой, которая зависит от диаметра диафрагмы связи, длина зонда связи или площади петли связи или площади всей петли связи, рис.5. Для характеристики степени связи резонатора с генератором и нагрузкой вводят понятие внешней добротности
. В объемном резонаторе энергия, накопленная в резонаторе, точно также расходуется на диссипативные потери внутри резонаторе, часть энергии отводится через элементы связи и поглощается в нагрузке и на внутреннем сопротивлении генератора. Причем соотношение между величинами потерь внутри резонатора с генератором и нагрузкой, которая зависит от диаметра диафрагмы связи, длина зонда связи или площади петли связи или площади всей петли связи, рис.5. Для характеристики степени связи резонатора с генератором и нагрузкой вводят понятие внешней добротности
 (4.11)
(4.11)
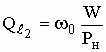
Обычно в системах СВЧ величины внутреннего сопротивления генератора и нагрузки равны и Qℓ = Qℓ1 = Qℓ2. Чем меньше величина внешней добротности, тем сильнее резонатор связан с нагрузкой, т.е. большая часть энергии расходуется в нагрузке.
Используя определение собственной , внешней и нагруженной добротности, легко получить соотношение, связывающее их
 (4.12)
(4.12)
Откуда следует, что при высокой собственной добротности Q0, величина нагруженной добротности приближенно равна ![]() .
.
Нетрудно видеть, что изменение внешней добротности Qℓ (степени связи резонатора с нагрузкой) приводит к изменению полосы пропускания 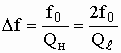 : чем меньше Qℓ, тем шире полоса пропускания объемного резонатора.
: чем меньше Qℓ, тем шире полоса пропускания объемного резонатора.
Величина рабочего ослабления на центральной частоте может быть выражена через Q0, Qн
 , дБ (4.13)
, дБ (4.13)
Полученное соотношение позволяет легко рассчитать собственную добротность Q0 по экспериментально полученным ![]() и ар0
и ар0
 (4.14)
(4.14)
Кратко рассмотрим принцип возбуждения объемного резонатора при помощи диафрагмы связи. Возбуждение резонатора происходит за счет передачи части энергии волны Н10, распространяющейся в подводящем волноводе, в резонаторе через отверстие в диафрагме связи. Так как в резонаторе может существовать колебание только на частоте f0mnp, то полная передача энергии ведется лишь на этой частоте, на всех других частотах энергия отражается от резонатора, причем чем больше отличие частоты от f0mnp, тем больше для нее коэффициент отражения. Можно считать, что искажение магнитного поля в отверстии диафрагмы, рис.8, возникает из – за двух магнитных дипольных моментов
![]() , индуцируемых в диафрагме касательной составляющей Нх магнитного поля волны Н10. Величина магнитного дипольного момента определяется магнитной поляризуемостью М отверстия связи. Магнитная поляризуемость круглого отверстия связи с диаметром d равна
, индуцируемых в диафрагме касательной составляющей Нх магнитного поля волны Н10. Величина магнитного дипольного момента определяется магнитной поляризуемостью М отверстия связи. Магнитная поляризуемость круглого отверстия связи с диаметром d равна
 (4.15)
(4.15)
Величина магнитной поляризуемости М однозначно определяет величину связи резонатора с проводящим волноводом [4]
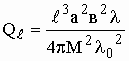 (4.16)
(4.16)
Диафрагмы связи искажают картину поля в резонаторе и при этом частота резонатора уменьшается. Для получения требуемой f0 длину резонатора следует рассчитывать с учетом влияния диафрагм связи.
а) Искажение Нх волны Н10 б) Магнитные дипольные
в проводящем волноводе ![]() , индуцированные в
, индуцированные в
диафрагме магнитным
полем, параллельным
плоскости диафрагмы
Нх
Рис. 8
1. Размеры поперечного сечения резонатора выбираются из условия одномодового режима основной волны прямоугольного волновода Н10
а = (0,6 ¸
0,8) l
0, где 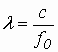
в = а/2
На практике обычно используют стандартные прямоугольные волноводы. В данной лабораторной работе для диапазона 5,6 – 8,3 ГГц используется стандартный волновод с а = 28,5 мм и в = 12,6 мм.
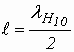 , где
, где  .
.
 ,
,
где: d
0 – глубина проникновения поля в проводник, для меди  , м
, м
При вычислении Q0 f0 следует подставлять в Гц; а, в – в метрах.


6. Диаметр диафрагмы связи находится по вычисленному значению внешней добротности Qℓ
![]() ,
,
где: 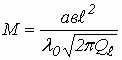 - магнитная поляризуемость диафрагмы связи.
- магнитная поляризуемость диафрагмы связи.
ℓкорр = ℓ - D ℓ,
где:  .
.