Глава 2. Триоды и тетроды. Полный ток в промежутке между электродами и во внешней цепи электровакуумных приборов. Как известно, в электронных лампах используется электростатическое управление электронным потоком, заключающееся в том, что изменение напряженности электрического поля в рабочем объеме лампы вызывает изменение высоты потенциального барьера для электронов в области объемного заряда около катода, а следовательно, изменение числа электронов, участвующих в создании тока. 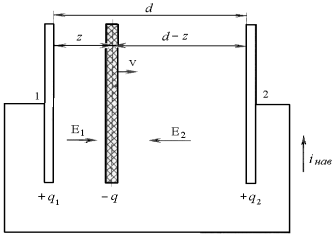Рис. 2.1 При переменных напряжениях на электродах лампы ток можно считать безынерционной функцией напряжения, если время пролета электронов в промежутке между электродами т много меньше периода переменного напряжения Т. Такой режим работы получил название квазистатического режима. Однако с ростом частоты время пролета может оказаться сравнимым с периодом переменного напряжения и больше его. В этом случае необходимо учитывать, что за время пролета электрона сильно изменяются напряжение на электродах и электрическое поле в пространстве между ними. Если амплитуда переменного напряжения велика, возможно, даже возвращение электронов к катоду. Теперь связь мгновенных значений токов и напряжений не соответствует связи в статическом или квазистатическом режиме. Для учета влияния времени пролета электронов на токи электродов применяется понятие наведенного тока, которое будет использовано и при рассмотрении специальных приборов СВЧ. Рассмотрим два плоских электрода (рис. 2.1) с равными потенциалами. Предположим, что от электрода 1 к электроду 2 движется тонкий электронный слой с общим зарядом — q. Вследствие явления электростатической индукции отрицательный заряд - q наводит на электродах положительные поверхностные заряды q 1 и q 2 , так что q1+ q2 = q. (2.1) Введем обозначения: ε 0 – диэлектрическая постоянная вакуума; S – площадь электродов; d– расстояние между электродами. Используя теорему Гаусса, можно определить напряженности поля у поверхности электродов: E1= q1 / ε0 S ; E2=q2 / ε0 S. (2.2) Очевидно, что E1 z - E2( d - z ) = 0, (2.3) где z – координата электронного слоя. Подставляя в это выражение E1 и Е2 из (2), получим q1 z - q2( d – z)=0. (2.4) Используя (2.1) и (2.4), найдем связь наведенных зарядов q1 и q2 с координатой электронного слоя z: q1 = q(1 – z/d); q2=qz/d. (2.5) Зависимость q1 и q2 от z линейная, при z=0, q1 = q и q2 = 0, а при z = d q1 = 0 и q2 = q. Вследствие движения слоя его координата z является функцией времени, при этом скорость слоя υ= dz/dt. Изменение зарядов q1 и q2 во времени означает, цепи течет ток iнав = dq2 / dt = - dq1 / dt , (2.6) называемый наведенным током. Используя (2.6) и (2.5), получим iнав = q υ /d (2.7) Наведенный ток возникает, как только электронный слои появляется в промежутке между электродами, и исчезает, когда электронный слой достигает второго электрода. Длительность импульса наведенного тока равна времени пролета электронов. При постоянной скорости электронов (υ = const) импульс iнав был бы прямоугольным, при линейной зависимости скорости от времени – треугольным. Используем (2.7) для нахождения наведенного тока во внешней цепи плоских электродов, если в пространстве между ними в рассматриваемый момент времени существует произвольное распределение плотности зарядов ρ(z, t), а не тонкий электронный слой. Применим (2.7) к бесконечно тонкому слою с толщиной dz и зарядом – dq, a затем произведем интегрирование. Наведенный ток, создаваемый элементарным слоем, по (2.7) diнав(t) =dqυ(z,t)/d. (2.8) Очевидно, что dq = ρ(z,t) S dz, поэтому из (2.8) получим 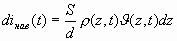(2.9) Создаваемый всеми электронными слоями в промежутке d в момент времени t наведенный ток 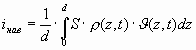(2.10) Подынтегральное выражение есть значение электронного тока в сечении z в момент времени t, связанное с переносом (конвекцией) электронов. Назовем его конвекционным током 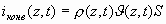(2.11) Подставляя (2.11) в (2.10), получим 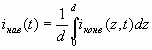(2.12) Если к электродам, показанным на рис. 1, приложить переменное напряжение u(t), то во внешней цепи кроме наведенного тока (2.12) будет существовать емкостный ток 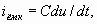(2.13) где C=ε0 S/d—емкость между электродами. Поэтому полный ток в цепи 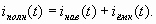(2.14) В (2.14) полный ток представлен как сумма наведенного и емкостного токов во внешней цепи, в отличие от обычного представления его суммой конвекционного тока (тока проводимости) и тока смещения, определяемых в зазоре между электродами: 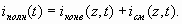(2.15) Выражение (12) позволяет вычислить наведенный ток во внешней цепи электродов, если известна зависимость конвекционного тока в зазоре от координаты и времени iконв(z,t). Наведенный ток в момент времени t равен усредненному по длине зазора значению конвекционного тока в этот момент времени. В частном случае, когда время пролета электронов много меньше периода переменного напряжения, можно считать, что iконв(z,t) практически не зависит от координаты и его можно вынести за знак интеграла. Тогда , т. е. наведенный ток совпадает с конвекционным. Поэтому в квазистатическом и статическом режимах нецелесообразно пользоваться понятием наведенного тока. В лампах СВЧ период переменного напряжения сравним с временем пролета электронов, поэтому конвекционный ток iконв(z,t) в зазоре сильно зависит от координаты г и наведенный ток не равен конвекционному. назад | оглавление | вперёд