4.2 Замедляющие системы
Наибольшее распространение в технике СВЧ получили замедляющие системы, представляющие собой линии передачи с периодически повторяющимися неоднородностями. Некоторые из них представлены на рис. 4.3, где 1 — спираль, 2 — гребенка, 3 —встречные штыри, 4 — сдвоенный меандр на диэлектрической подложке, 5 — диафрагмированный волновод, 6 —диафрагмированный волновод с индуктивными щелями связи, 7 — “лист клевера”, 8 — меандр на диэлектрической подложке.
Широко используется замедляющая система в виде цилиндрической спирали. Эта замедляющая система была использована Р. Компфнером в 1944 г. в первой ЛБВ, и сейчас большинство серийно выпускаемых ЛБВ тоже использует спиральную замедляющую систему, что объясняется многими ее достоинствами. Ни, одна из известных замедляющих систем не может конкурировать, со спиралью в отношении широкополосности. При упрощенном рассмотрении процессов в такой системе можно предполагать, что волна Т распространяется со скоростью света с вдоль спирального проводника. Пусть D будет средний диаметр спирали, a L – ее шаг. Тогда время, за которое волна обегает один виток,
Если шаг спирали много меньше диаметра, т. е. L<<πD, имеен t<<πD/c. Волна за то же время проходит вдоль оси спирали путь, равный L. Следовательно, фазовая скорость волны ve вдоль оси спирали равна L/t или vф=cL/πD.
Обычно замедляющую систему характеризуют коэффициентом замедления Кзам, равным отношению скорости света к фазовой скорости замедленной электромагнитной волны.
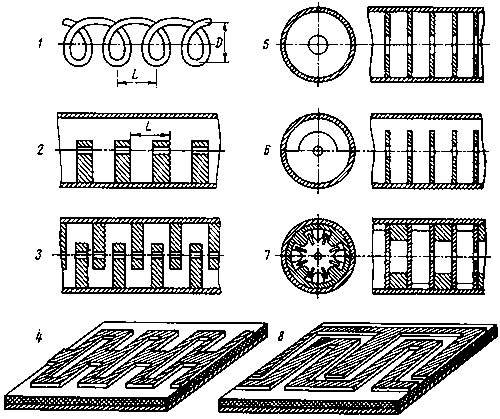
Рис. 4.3
Тогда Kзам=c/vф=πD/L (4.2)
Коэффициент замедления тем больше, чем больше отношение длины витка к шагу спирали. Изменяя диаметр спирали D и ее шаг L, можно в широких пределах изменять коэффициент замедления.
Более точный анализ распространения электромагнитных волн вдоль спирали показывает, что спираль обладает дисперсией, т. е. фазовая скорость волны в спирали зависит от частоты. Но на достаточно высоких частотах (4.2) дает хорошее приближение.
Рассмотрим некоторые общие закономерности распространения электромагнитных волн в замедляющих системах. Замедляющие системы представляют собой периодические структуры, имеющие свойства полосовых фильтров с бесконечным числом полос пропускания. В приборах используется чаще всего полоса, пропускающая самые низкие частоты, она называется основной. Остальные полосы называются высшими.
Поле в периодической структуре удовлетворяет теореме Флоке, которая утверждает, что среди решений уравнений Максвелла, удовлетворяющих граничным условиям, всегда найдется такое решение, при котором поля в соседних ячейках отличаются лишь постоянным множителем p=e-r, т. е. E(z+L)=e-r Е(г). В полосе пропускания для систем без потерь величина Г=iψ – мнимая. Это означает, что поле в соседних ячейках отличается лишь сдвигом по фазе на угол ψ. Введем обозначение ψ=β0L (β0—постоянная распространения волны) и умножив обе части равенства на ехрiβo(L+z), при этом заметим, что функция E0(z)=E(z)ехрiβoz=E(z)ехрiβo(z+L) — периодическая, а ее период совпадает с периодом структуры L. Отсюда следует, что поле в системе E(z) можно представить в виде произведения двух периодических функций: E0(z) и ехрiβoz. Учитывая и временной множитель ехрiωt, можно записать
E(z,t)=E0(z)ei(ωt-βoz) (4.3)
Функция E0(z) — периодическая, L — ее период. Разложение E0(z) в ряд Фурье дает
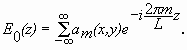(4.4)
где
Подставляя (4.4) в (4.3), получим
(4.5)
Распределение поля в системе представлено в виде суммы бесконечного числа бегущих волн с амплитудами am(x,у) и постоянными распространения
(4.6)
Эти волны называются пространственными гармониками. Их совокупность удовлетворяет периодическим граничным условиям. Решение в виде одной пространственной гармоники не может удовлетворить граничным условиям. Все гармоники изменяются с одной и той же частотой. Каждой пространственной гармонике соответствует своя фазовая скорость, которая определяется соотношением
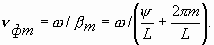(4.7)
Групповая скорость всех пространственных гармоник одинакова:
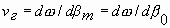(4.8)
Зависимость фазовой скорости (или коэффициента замедления) от частоты в свободном пространстве называется дисперсией замедляющей системы, а графики этих зависимостей — дисперсионными характеристиками или кривыми дисперсии. Каждой пространственной гармонике соответствует определенная ветвь дисперсионной характеристики.
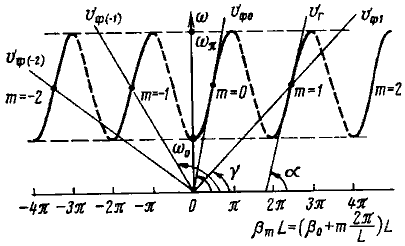
Рис. 4.4
Волна (или пространств венная гармоника), у которой направления групповой и фазовой скоростей одинаковые, называется прямой волной, волна с противоположными направлениями скоростей — обратной волной.
В зависимости от знака производной d|vфm|/dω дисперсия может быть нормальной (d|vфm|/dω<0) и аномальной (d|vфm|/dω >0). При увеличении частоты нормальная дисперсия характеризуется уменьшением абсолютного значения фазовой скорости, а аномальная — ростом. Для всех обратных гармоник дисперсия аномальная, прямые гармоники могут иметь как нормальную, так и аномальную дисперсию.
На рис 4.4. показана дисперсионная характеристика замедляющей системы. По оси абсцисс отложен фазовый сдвиг на один период замедляющей системы βmL, определяемый (4.6), а по оси ординат—частота ω. Сплошные кривые относятся к гармоникам т=0, ±1, ±2. Нулевая гармоника (m=0) соответствует изменению угла от 0 до π. Эти пределы в соответствии с теорией фильтров определяют полосу пропускания, заключенную между ω0 и ωπ. Сдвиг фазы для гармоники m=+1 по определению (4.6) на 2π больше, чем при т=0, поэтому кривая для т=+1 существует в пределах (2
3)π.Соответственно смещаются на 2π вправо кривые при каждом увеличении на единицу номера т. Переход от т=0 к т=-1 эквивалентен смещению кривой в область фазы от -π до -2π и т. д. Полоса пропускания для всех пространственных гармоник одинакова и равна полосе пропускания замедляющей системы.
Фазовая скорость гармоники с учетом (4.7) пропорциональна тангенсу угла наклона у прямой, проведенной через начало координат и точку дисперсионной кривой для выбранной частоты <0. Групповая скорость гармоники пропорциональна производной в данной точке, т. е. tg a. Очевидно, что на границах полосы пропускания групповая скорость гармоник равна нулю (экстремальные точки кривых). Групповая скорость всех пространственных гармоник при данной частоте ω одинакова и положительна. Для варианта замедляющей системы, дисперсионная характеристика которой приведена на рис. 4.4, наибольшая фазовая скорость у нулевой гармоники. С увеличением положительного номера т фазовая скорость уменьшается, фазовые скорости гармоник m= -1, -2 отрицательны (противоположны направлению групповой скорости) и также уменьшаются с ростом номера. В рассматриваемом случае гармоники m=0, +1, +2 — прямые, а m= -1, -2 — обратные.
Используя дисперсионные кривые, можно выяснить зависимость фазовой скорости любой пространственной гармоники от частоты. В нашем примере прямая нулевая гармоника имеет нормальную дисперсию (фазовая скорость уменьшается с ростом частоты). Обратные гармоники (т= -1, -2) обладают аномальной дисперсией. Легко убедиться, что для прямой гармоники т=+2 вблизи границ пропускания дисперсия нормальная, а в остальной области аномальная.
Важной характеристикой замедляющей системы является сопротивление связи, которое характеризует эффективность взаимодействия электронного потока с полем в замедляющей системе. По определению сопротивление связи
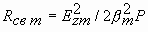(4.9)
Чем больше продольная составляющая напряженности электрического поля Еzm в месте прохождения электронного пучка при данном потоке мощности Р в системе, тем больше сопротивление связи.
Если выразить поток мощности через запасенную энергию W на единицу длины системы и групповую скорость (P=vгW), то сопротивление связи
(4.10)
Так как групповая скорость входит в выражение для сопротивления связи, то Rсв тем больше, чем меньше крутизна tg a дисперсионной характеристики (см. рис. 4.4).
Изменяя скорость электронов ve регулировкой ускоряющего напряжения, можно выполнить условия синхронизма для любой пространственной гармоники. Так как фазовая скорость нулевое пространственной гармоники наибольшая, то для взаимодействия с ней необходима наибольшая скорость электронов, что требует высокого ускоряющего напряжения. Для взаимодействия электронного потока с высшими гармониками замедляющей систем скорость электронов должна быть меньше и соответственно меньше будут ускоряющие напряжения. Однако взаимодействие с высшими пространственными гармониками для систем 1, 2, 6 рис. 4.3 получается неэффективным, поскольку они имеют малое сопротивление связи. Поэтому в приборах СВЧ используются в основном нулевая и плюс первая или минус первая гармоника. Прямые пространственные гармоники используются в ЛБВ, а обратные — в ЛОВ. Дисперсионная характеристика замедляющей системы определяют ширину полосы частот усилителя и диапазон электронной перестройки генератора.
Строгий метод расчета замедляющих систем основывается на решении уравнений Максвелла с учетом конкретных граничных условий. Однако сложность конфигурации большинства замедляющих систем затрудняет решение этой задачи. Часто применяются различные приближенные методы, среди которых широко распространен метод эквивалентных схем. Замедляющая система представляется эквивалентной схемой в виде цепочки ячеек фильтра с сосредоточенными постоянными. Этот метод позволяет оценить ширину полосы пропускания, а также качественно определить влияние отдельных элементов замедляющей системы на характеристики.
назад | оглавление | вперёд