9.3 Открытый оптический резонатор. Открытым оптическим резонатором называют систему, состоящую из двух обращённых друг к другу отражающих поверхностей, в которой могут возбуждаться электромагнитные колебания оптического диапазона. Отражающими поверхностями могут быть зеркала различной формы (плоские, сферические, параболические), грани призм полного внутреннего отражения, границы раздела сред с различными показателями преломления. Простейшим открытым оптическим резонатором является система из двух параллельных зеркал, находящихся на определённом расстоянии друг от друга. Эффективное взаимодействие электромагнитного поля с активной средой осуществляется при помещении её в резонатор, который должен быть таким, чтобы можно было разместить внутри него достаточное количество активного вещества. Активное вещество может заполнять рабочий объём резонатора частично или полностью. Задача резонатора лазера – обеспечить, чтобы возникающее внутри него вынужденное излучение многократно проходило через активную среду, способную усиливать проходящее через неё излучение. Таким образом, с помощью резонатора получается положительная обратная связь. Для вывода полезного излучения из резонатора его зеркала делаются частично прозрачными (полупрозрачными). Резонатор во многом определяет основные свойства выходного излучения: степени монохроматичности и когерентности, направленность и мощность. Нормальные типы колебаний (моды) резонатора можно рассматривать как результат интерференции плоских волн, распространяющихся от одного зеркала к другому. В результате в резонаторе образуются стоячие волны. Нормальные типы колебаний открытого резонатора обозначают Тmnq, чтобы показать, что векторы электрического и магнитного полей в большинстве случаев перпендикулярны продольной оси резонатора. Индексы m,n,q – целые числа; q равно числу полуволн, укладывающихся вдоль оси резонатора между его зеркалами. Типы колебаний с различными m и n называют поперечными. Они отличаются друг от друга распределением амплитуды и фазы поля на поверхностях зеркал, а также дифракционными потерями. Типы колебаний, имеющие одни и те же значения m и n, но разное q, называют продольными. Они отличаются друг от друга резонансной частотой. Интервал между частотами двух соседних, различающихся по величине q на единицу, продольных колебаний в резонаторе с плоскими параллельными бесконечно протяженными зеркалами, составляет где c – скорость света; L – расстояние между зеркалами. В лазерах сначала применялись резонаторы с плоскими зеркалами. В настоящее время такие резонаторы используются в твердотельных и полупроводниковых лазерах. Одним из достоинств резонаторов с плоскими зеркалами является максимальная направленность выходного излучения. Резонаторы, образованные двумя сферическими зеркалами с равной кривизной, находящимися друг от друга на расстоянии радиуса кривизны, называются конфокальными резонаторами. Часто используются полусферические резонаторы, у которых одно зеркало плоское, а второе – сферическое. Длина такого резонатора равна половине радиуса кривизны сферического зеркала. Резонатор имеет низкие потери и мало критичен к изменению расстояния между зеркалами. Открытые резонаторы по сравнению с закрытыми тех же размеров имеют значительно более разряжённый спектр собственных частот. Условия самовозбуждения, как обычно, включают в себя баланс фаз и баланс мощностей. Рассмотрим резонатор на рис.9.7, полностью активной средой. Обозначим через Г1 и Г2 комплексные коэффициенты отражения от зеркал, L – расстояние между зеркалами. Предположим, что в некоторый момент времени вблизи зеркала 1 возникло спонтанное излучение, которое распространяется к зеркалу 2. Поле А 1 при движении внутри резонатора взаимодействует с веществом и у зеркала 2 будет иметь вид где ixp = ik - постоянная распространения; xа – показатель усиления активной среды; k – фазовая постоянная; аа – показатель потерь активной среды, учитывающий потери вследствие рассеяния излучения на неоднородностях после отражения от зеркала 2. . Здесь коэффициент x учитывает дифракционные потери при отражении от зеркала. 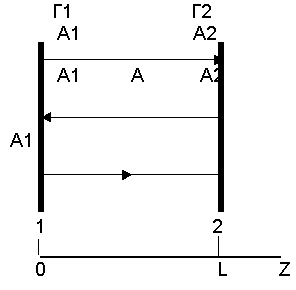После А¢ 2 при обратном распространении к зеркалу 1 вновь усиливается в активной среде и после отражения от зеркала 1 можно записать (9.6) Рис. 9.7 Из (1) получаем условие стационарности колебаний (9.7) комплексные коэффициенты отражения представим в виде, где Г1, Г2 – модули коэффициентов отражения; D j и D j 2 - изменение фазы волны при отражении от зеркал. Подставляя Г1, Г2 и Xp в (9.7) и учитывая, что k = 2 P / l , после разделения действительной и мнимой частей (9.7) получаем соответственно условия баланса фаз и амплитуд: (9.8) (9.9) Условие (9.8) означает, что волны, пройдя путь 2L в резонаторе и дважды отразившись от зеркал, получают фазовый сдвиг, кратный целому числу периодов. В генераторе создаётся положительная обратная связь. Условие баланса фаз определяет частоту лазерного излучения. Так как (9.8) выполняется на любой резонансной частоте оптического резонатора, то на каждой из этих частот может быть генерация, если будет выполнено условие баланса амплитуд. Согласно (9.9) колебания в лазере будут существовать лишь в том случае, если усиление в активной среде компенсирует все потери в резонаторе. Логарифмируя (9.9) , получаем 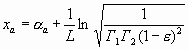(9.10) Второе слагаемое в (9.10) учитывает потери в зеркалах, в том числе на полезное излучение. Мощность генерации Рген в стационарном режиме, определяемая из баланса мощностей, равна сумме мощностей потерь в среде и зеркалах и пропорциональна (аа + а3). Если пренебречь рассеянием и поглощением в зеркалах, то мощность потерь будет равна мощности излучения, выходящего из резонатора через зеркало. Последнюю назовём мощностью излучения Ризл. Pизл/ Pген= a 3 / ( a а+ a 3 ) . Выходящая из резонатора мощность Ризл зависит от коэффициентов пропускания зеркал и при увеличении а3 растёт, достигая максимума, а затем уменьшается до нуля, когда потери станут настолько большими, что условие самовозбуждения не выполняется. Таким образом, можно подобрать оптимальный режим работы лазера. назад | оглавление | вперёд