Если x(t) – сигнал на входе канала связи, а y(t)=x(t)+n(t) – сигнал на его выходе (n(t) – аддитивная помеха), то скорость передачи информации по непрерывному каналу связи будет определяться выражением (23), в котором величину 1/t надо заменить на 2Fmax ( или 2Fk , предполагая, что  источник сигнала согласован с каналом и его полоса пропускания Fk= Fmax)

                   ,                           (37)

где, как и ранее, H(y) – это энтропия выходного сообщения, H(y/x) – энтропия шума (почему она так называется, будет видно из дальнейшего изложения).

Пропускная способность равна максимально возможной скорости передачи по каналу связи, когда источник сигнала полностью согласован с характеристиками канала связи:

                   .                                (38)

Максимум H(y) достигается в случае гауссовского закона распределения случайной величины y. При этом

                   .                                    (39)

При учёте влияния помехи необходимо рассматривать наихудший случай, когда помеха распределена также по гауссовскому закону.

Условная вероятность w(y/x) – это попросту вероятность распределения случайной величины y при якобы известном заранее значении x, хотя величина x является случайной. Но, так как y(t)=x(t)+n(t), можно записать

                   ,

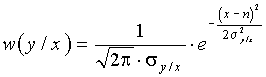где s2y/x – дисперсия величины y при известном x, т.е. дисперсия помехи s2n.

Определим условную энтропию H(y/x)

         .

В этом выражении предполагается, что x известно заранее. Таким образом, величина x в приведенном выражении является попросту математическим ожиданием величины y. Однако известно, что энтропия непрерывного случайного процесса от математического ожидания не зависит.

Тогда получаем, что

.

Отсюда видно, почему условная энтропия H(y/x) называется энтропией шума.

Для гауссовского закона распределения помехи максимальное значение энтропии шума, в соответствии с (35), будет равно

.                                (40)

Подставляя (39) и (40) в (38), получаем         .

Перенося число 2 под знак логарифма, получим 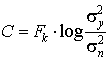. В этом выражении s2n=Pп – мощность помехи, а s2y=s2x+s2n=Pс+Pп, где Pс – мощность сигнала на выходе канала связи. С учётом этого получаем окончательно формулу для вычисления пропускной способности непрерывного канала связи (формулу Шеннона):

                   .                                                   (41)

В заключение можно отметить следующее.

Для достижения скорости передачи информации по непрерывному каналу связи, близкой к пропускной способности канала связи, сигнал x(t) по статистической структуре должен быть близок к флюктуационной помехе (белому шуму) с гауссовским законом распределения.

Вопросы к главе 14

1. От чего зависит пропускная способность непрерывного канала связи?
2. Приведите формулу для нахождения пропускной способности непрерывного канала связи.
3. Как изменяется пропускная способность непрерывного канала связи при увеличении  эффективной полосы пропускания канала?
4. Какие предъявляются требования к сигналу (его статистической структуре), чтобы приблизить скорость передачи непрерывного сигнала к пропускной способности канала?

назад | оглавление | вперёд