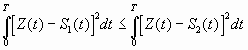Важным показателем систем связи является помехоустойчивость, т.е. способность системы связи противостоять вредному влиянию помех.

При рассмотрении вопросов передачи и приёма двоичных последовательностей полагают, что источник дискретных сообщений вырабатывает на своём выходе последовательность двух элементов (символов) – единицы и нуля с соответствующими вероятностями их появления p(1)и p(0).

Для их передачи используют два различных сигнала S1(t) и S2(t), длительность каждого из которых равна длительности элемента последовательности Т.

На вход приёмного устройства поступает смесь переданного сигнала и помехи, т. е.

Z(t) = Si (t) + x (t).

В курсовой работе рассматривается канал с постоянными параметрами и аддитивной помехой типа гауссовского белого шума. Такие (гауссовские) каналы являются достаточно хорошей моделью многих реальных каналов передачи цифровой информации, в частности, кабельных, оптических, радиорелейных, космических и других.

Для количественной оценки влияния помех и других факторов, вызывающих отличие принятой последовательности от переданной, вводится критерий оценки качества принятой информации. При передаче дискретных сообщений за такой критерий принимают вероятность ошибки приёма одного элемента двоичной последовательности.

Приёмник, в результате анализа принятой конкретной реализации Z(t) на интервале времени 0 £ t £ T , должен установить, какой из возможных сигналов Si (t) (S1(t) или S2(t)) присутствует на его входе, и в соответствии с этим принять решение о приеме символа 1 или 0. Это классическая задача теории связи – задача различения двух сигналов. В случае, когда один из сигналов тождественно равен нулю (например, ДАМ), имеем задачу обнаружения сигнала в интервале времени 0 £ t £ T на фоне помех.

Для различения сигналов в приёмнике необходимо (с допустимой погрешностью) устанавливать начало и конец интервала анализа каждой реализации Z(t), поступающей на вход приёмника. Такая задача решается устройством синхронизации, которое позволяет определять начало и окончание каждого элемента сигнала (сообщения) в принятой последовательности.

Алгоритм различения двух и более сигналов на фоне белого гауссовского шума имеет ясный физический смысл: наиболее вероятным переданным сигналом считается тот сигнал, который меньше отличается (в среднеквадратичном смысле) от принятого сигнала. Таким образом, оптимальный приемник минимизирует среднюю вероятность ошибки. В аналитической форме алгоритм оптимального приёмника при равновероятных сигналах имеет вид

Если 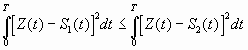, то Z(t) º S1(t), иначе S2(t), (2.1)

т.е. решение принимается в пользу сигнала S1(t).

При этом считается, что все параметры сигнала в точке приёма известны, т. е. известны его форма, амплитуда, частота, задержка во времени и начальная фаза (приём полностью известных сигналов). Неизвестным в этом случае является только то, какой из возможных сигналов передаётся на данном интервале
наблюдения 0 £ t £ T .

Выражение (2.1) позволяет представить алгоритм в виде структурной схемы оптимального приёмника, т. е. решить задачу оптимального синтеза.

Для передачи элементов двоичного кода (0 или 1) обычно используются сигналы с дискретной амплитудной модуляцией (ДАМ), частотной модуляцией (ДЧМ) и фазовой модуляцией (ДФМ или ДОФМ). Для конкретного вида используемых сигналов ДАМ, ДЧМ, ДФМ алгоритм оптимального приёмника и соответствующая ему структурная схема получаются на основании общего алгоритма (2.1), при этом оптимальный приёмник должен вычислять значение функции взаимной корреляции вида

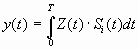. (2.2)

Для этого используется или коррелятор, или согласованный фильтр, которые обеспечивают одинаковую помехоустойчивость, т. е. эквивалентны.

В процессе передачи элементы кода искажаются помехами, причем, наблюдаются ошибки двоякого рода:

1. При передаче элемента 0 может быть ошибочно принят элемент 1, вероятность такого события (перехода 0® 1) обозначим через p(1/0) — вероятность приема 1 при передаче 0.
2. При передаче элемента 1 может быть ошибочно принят элемент 0, вероятность такого события (перехода 1® 0) обозначим через p(0/1) — вероятность приема 0 при передаче 1.

Средняя вероятность ошибки определяется по формуле

pош = p(0)× p(1/0) + p(1)× p(0/1). (2.3)

В дальнейшем будем считать, что априорные вероятности передачи элементов кода равны, то есть p(0) = p(1) = 0,5, при этом

pош = 0,5[p(1/0) + p(0/1)]. (2.4)

Помеху в канале связи будем считать флуктуационной с нормальным законом распределения мгновенных значений

w (x ) = 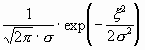. (2.5)

Вероятность ошибки зависит: от вида модуляции, способа детектирования (когерентный, некогерентный), способа фильтрации сигналов в приёмнике (оптимальный фильтр, неоптимальный фильтр), мощности Pс (энергии Eс) сигнала, мощности Pп (спектральной плотности N0) помехи.

Если в приёмнике используется неоптимальный фильтр, вероятность ошибки зависит от величины отношения мощности сигнала к мощности помехи (отношение сигнал/шум по мощности) h2 = Pс / Pп.

При использовании в приёмнике оптимального фильтра вероятность ошибки определяется величиной отношения энергии элемента сигнала к спектральной плотности мощности помехи h02 = Eс / N0 = PсTс/ N0.

В приёмнике с оптимальным фильтром отношение сигнал/шум больше, чем в приёмнике с неоптимальным фильтром и, соответственно, помехоустойчивость выше.

Приёмник с оптимальным фильтром и когерентным способом приёма обеспечивает потенциальную помехоустойчивость для заданного вида модуляции.

Помехоустойчивость приема сигналов ДАМ, ДЧМ, ДФМ, ДОФМ в указанных выше условиях можно определить, вычисляя среднюю вероятность ошибки следующим образом.

2.2 Дискретная амплитудная модуляция

Элементами сигналов ДАМ являются посылки (кодовый элемент “1”) и паузы (кодовый элемент “0”)

0 £ t £ T,

где Т – длительность элемента сигнала.

Некогерентный прием

Прием сигнала ДАМ в этом случае осуществляется путем сравнения уровня сигнала после амплитудного детектора (детектора огибающей) с некоторым пороговым уровнем Uп решающей схемы приемника (рис. 2). Ошибки возникают в случаях:

1 При передаче посылки огибающая суммы сигнала и помехи (Eсп) оказывается меньше порогового уровня Uп (переход 1® 0).

2 При передаче паузы огибающая помехи Eп оказывается больше Uп (переход 0® 1).

Вероятности этих событий определяются через соответствующие распределения значений огибающих (рис. 3,а и рис 3,б)

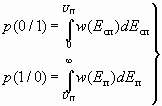, (2.6)

где w(Eсп)– плотность распределения огибающей суммы сигнала и помехи, которая, как известно, определяется обобщенным законом Релея (Релея-Райса),

,

w(Eп) – плотность распределения огибающей помехи, определяется простым законом Релея.

.

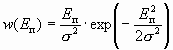Средняя вероятность ошибки с учетом (2.4) и (2.6) равна

pошАМнкг = 0,5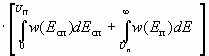. (2.7)

Значение pош зависит от порогового уровня Uп решающей схемы. Можно показать, что вероятность ошибки минимальна, когда Uп (при a2 » s 2), т.е в этом случае Uп имеет оптимальное значение. При этом окончательно получаем

pошАМнкг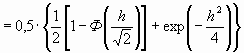, (2.8)

где – отношение мощностей сигнала и помехи (отношение сигнал / шум), а

Ф(z)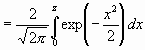

– табулированный интеграл вероятностей.

Зависимость pош = f(h) при некогерентном приеме показана на рис. 5 (кривая 1).

Если h2 » 1, то

pош.АМ нкг » . (2.9)

Максимальная помехоустойчивость при приеме сигналов ДАМ наблюдается в том случае, если применяется оптимальная фильтрация сигналов. В этом случае необходимо в ф-ле (2.9) вместо подставить , равное

, (2.10)

где – энергия элемента сигнала,

N0 – спектральная плотность мощности помехи.

Когерентный прием

и ,

где w(x/a) и w(x)-плотности распределения вероятностей мгновенных значений сигналов на выходе детектора при приёме посылки и паузы соответственно

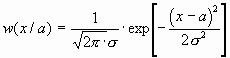и .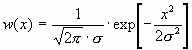

Средняя вероятность ошибки будет равна

pошАМкг = 0,5.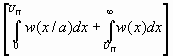

При оптимальном значении порогового уровня решающей схемы , вероятность ошибки минимальна и равна

pошАМкг = , (2.11)

где – отношение сигнал / шум.

Зависимость pошАМ = f(h) при когерентном приёме показана на рис. 6 (кривая 2).

При когерентном приеме достигается потенциальная помехоустойчивость, если в приемнике осуществить оптимальную фильтрацию сигнала. При этом достигается максимальное отношение сигнал /шум

,

и в ф-ле (2.11) h заменяется на h0.

2.3 Квадратурная амплитудная модуляция (КАМ)

В последние годы в аппаратуре связи стала широко применяться квадратурная амплитудная модуляция (КАМ). Промодулированный сигнал представляет собой сумму двух ортогональных несущих: косинусоидальную и синусоидальную, амплитуды которых принимают независимые дискретные значения. Рассмотрим в качестве примера сигнал для КАМ - 16, где число 16 означает количество вариантов суммарного сигнала.

Пусть шаг между разрешенными уровнями сигнала составляет один вольт. Векторная диаграмма возможных состояний сигнала для этого случая представлена на рис 2.

Рассмотрим случай воздействия на сигнал аддитивной гауссовой помехи. Условные плотности вероятности представляют собой шестнадцать возвышенностей. На рис. 2 представлена область правильного приёма ² 6² -го сигнала. Для оценки вероятности ошибки рассмотрим сечение двухмерной плотности вероятности при y = +1 В. (см. рис. 3).

Вероятность того, что уровень сигнала по оси X (амплитуда косинусоидальной составляющей) превысит Uï3 = 2 В, будет равна

p{ x > Uï3 } = p1 =,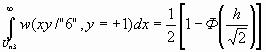

где ;

D U – расстояние между соседними сигналами (в приведенном примере D U = 2 В);

s 2 – мощность шума.

Вероятность того, что уровень сигнала по оси X окажется меньше Uï2, áудет равна

py=1 { x < Uï2} = p2 =.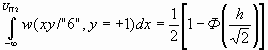

Аналогичные выражения для вероятности ошибки могут быть получены при анализе изменения сигнала по оси Y .

Ошибочное решение при приёме ² 6² —го сигнала произойдет в следующих ситуациях :

1. Принимаемый сигнал превысит Uï2 ïо оси X или по оси Y , или по обеим осям вместе, т.е. р> = p2 + p2 – p2 × p2.
2. Принимаемый сигнал будет меньше U0 по оси X, по оси Y , или по обеим осям вместе, т.е. р< = p2 + p2 – p2 × p2.

Верхняя оценка вероятности ошибочного решения может быть определена соотношением:

р = р< + p> = 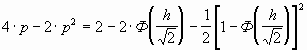. (2.12)

При строгом учёте всех ситуаций средняя вероятность ошибок будет несколько меньше.

В реальных каналах связи р< = p> << 1. В этом случае

. (2.13)

2.4 Дискретная частотная модуляция

Элементами сигнала при ДЧМ являются

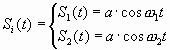0 £ t £ T.

В приёмнике сигналы разделяются с помощью канальных полосовых фильтров, настроенных на частоты w 1 и w 2, с последующим детектированием.

Некогерентный приём

При приёме сигналов ДЧМ в одном из фильтров всегда присутствует сумма сигнала и помехи, а в другом только помеха. Ошибка при регистрации сигнала, очевидно, будет в том случае, когда огибающая помехи в фильтре без сигнала превысит огибающую суммы сигнала и помехи в фильтре с сигналом (рис. 2, а и б).

Считаем, что мощности сигнала и помехи в каждом из фильтров одинаковы. Тогда вероятности искажения символов " 1" и " 0" будут одинаковы, т.е. p(0/1) = p(1/0) (канал симметричный).

Вероятность того, что огибающая помехи в фильтре без сигнала превысит огибающую суммы сигнала и помехи в другом фильтре, равна (рис. 5)

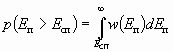. (2.14)

В выражении (2.14) огибающая суммы сигнала и помехи является случайной величиной, имеющий обобщенный закон распределения Релея. Поэтому для определения вероятности ошибки необходимо усреднить вероятность p(Eп > Eсп) по всем значениям Eсп:

.

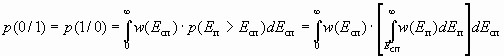Подставляя сюда выражения для w(Ecп) и w(Eп), получим

,

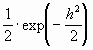где h2 – отношение сигнал / шум на выходе фильтра с сигналом.

Для случая равновероятных сообщений средняя вероятность ошибки будет равна

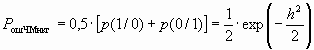. (2.15)

Зависимость pошЧМ = f(h) показана на рис. 6 (кривая 3). Максимальная помехоустойчивость при некогерентном приёме сигналов ДЧМ достигается в случае, если осуществляется оптимальная фильтрация сигнала, при этом в ф-ле (2.15) h2 заменяется на h02.

Когерентный приём

При когерентном приёме сигналов ДЧМ на помехоустойчивость влияют только синфазные с сигналом составляющие помех x1 в фильтре w 1 и x2 в фильтре w 2. Эти составляющие имеют нормальный закон распределения амплитуд с одинаковыми дисперсиями

.

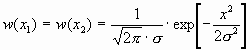Вероятность превышения синфазной составляющей помехи в фильтре без сигнала x2 составляющей суммы сигнала и помехи в фильтре с сигналом (a + x1) равна

.

Для определения средней вероятности ошибки необходимо усреднить вероятность p(x2 > (a + x1)) по всем значениям случайной величины (a+x1), при этом для случая флуктуационной помехи (и симметричного канала связи) получим:

,

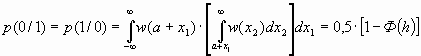где h2 – отношение сигнал / шум.

Средняя вероятность ошибки равна

pошЧМкг = 0,5× [ p(0 /1) + p(1/ 0)] = 0,5× [1 – Ф(h)]. (2.16)

Зависимость pошЧМ = f (h) для когерентного приёма показана на рис. 6 (кривая 4).

При когерентном приёме сигналов ДЧМ достигается потенциальная помехоустойчивость, если используется оптимальная фильтрация сигналов. В этом случае в ф-ле (2.16) вместо h подставляют h0.

2.5 Дискретная фазовая модуляция

Элементами сигнала при ДФМ являются

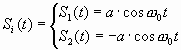0 £ t £ T.

Приём сигналов фазовой модуляции возможен только с помощью синхронного (когерентного) детектора, различающего фазы принимаемых сигналов. Вероятности переходов р(1/ 0) и р(0 /1) при флуктуационной помехе в канале связи одинаковы и равны

.

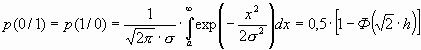Соответственно средняя вероятность ошибки равна

. (2.17)

Максимальная помехоустойчивость сигналов ДФМ, равная потенциальной, достигается при оптимальной фильтрации сигналов, при этом в ф-ле (2.17) вместо подставляем .

2.6 Дискретная относительная фазовая модуляция

При использовании в системе связи дискретной ОФМ на передаче включается блок внесения относительности на входе модулятора, а на приёме относительность снимается либо по высокой частоте (в фазовом детекторе), либо по низкой частоте (после фазового детектора). Первый способ приёма называется методом сравнения фаз (некогерентный приём), второй – методом сравнения полярностей (когерентный приём).

При передаче дискретных двоичных сообщений сигналами ОФМ характерно, что неправильный приём одного символа сообщения ведёт к сдвоенной ошибке. Средняя вероятность ошибки находится из следующих выражений:

- для метода сравнения фаз,

рош сф

- для метода сравнения полярностей

pош сп = 2× pфм× (1- pфм) » 2× pфм, (2.18)

здесь рфм – средняя вероятность ошибки при классической ДФМ, которая определяется по ф-ле (2.17).

Таким образом, вероятность неправильного приёма символа для ДОФМ с приёмом по методу сравнения полярностей примерно в 2 раза больше, чем при ДФМ.

На рис. 4.4 приведены кривые зависимости рошофм = f (h).

2.7 Прием сигналов методом многократных отсчетов

Для повышения помехоустойчивости приёма дискретных двоичных сообщений решение о переданном символе принимается не по одному отсчёту на длительности элемента сигнала 0 £ t £ T , а по нескольким, в общем случае по n некоррелированным отсчётам Z1, Z2, ... , Zn, принимаемой смеси сигнала и помехи (метод дискретного накопления). При этом отсчёты берутся через интервал D t, равный интервалу корреляции помехи t 0x , т.е. они будут некоррелированными. Для принятия решения о переданном символе должна быть определена совместная n-мерная плотность распределения вероятностей для заданных n отсчётов, т. е. wn (Z /1) и wn (Z /0). Для случая гауссовского стационарного шума некоррелированные отсчёты смеси сигнала и шума будут независимыми. Следовательно, wn (Z /ai) равна произведению одномерных плотностей распределения каждого из отсчётов, т. е.

wn (Z /ai) = wn (Z1 /ai) × wn (Z2 /ai) × ... × wn (Zn /ai).

Приём методом многократных отсчётов позволяет по сравнению с принятием решения по одному отсчёту увеличить отношение сигнал / шум в n раз,
т. е. hn2 = n× h12 . Это обусловлено тем, что мощность сигнала возрастает в n 2 раз, а мощность помехи — только в n раз. Характерно, что при приёме дискретных сигналов методом многократных отсчётов можно получить сколь угодно значительное отношение сигнал/шум (и, соответственно, высокую помехоустойчивость) путём увеличения числа отсчётов на длительности элемента сигнала. Однако очевидно, что это требует увеличения длительности элемента сигнала тоже в n раз, что, в свою очередь, приводит к снижению скорости передачи сообщений также в n раз по сравнению с вариантом принятия решения по одному отсчёту. Таким образом, реализуется принцип обмена скорости передачи дискретных сообщений на помехоустойчивость путём увеличения энергии элемента сигнала Eс = PсT.

2.8 Фильтрация дискретных сигналов

Помехоустойчивость приёма дискретных сигналов, как это было показано выше, определяется отношением сигнал / помеха на входе решающего устрой-ства.

Наибольшее отношение сигнал / помеха, равное отношению энергии элемента сигнала к спектральной плотности флуктуационной помехи, обеспечивают так называемые оптимальные фильтры.

Известно, что амплитудно-частотная характеристика оптимального фильтра для приёма дискретных сигналов совпадает с точностью до постоянного множителя C1 с амплитудным спектром сигнала

K(w ) = C1× S(w ),

а импульсная характеристика представляет собой зеркальное отображение временной функции сигнала, задержанное на длительность сигнала Т.

Для прямоугольного радиоимпульса в качестве оптимального фильтра может быть использован колебательный контур высокой добротности, для которого динамическая амплитудно-частотная характеристика определяется выражением

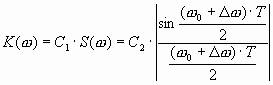, (2.19)

а эффективная полоса пропускания равна D fэф = 1/ T.

Амплитудно-частотная характеристика фильтра, оптимального для прямоугольного видеоимпульса, определяется выражением

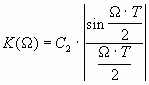, (2.20)

а эффективная полоса пропускания равна D fэф = 1/ 2T.

Иногда оптимальные фильтры трудно реализуемы. В этом случае применяют так называемые квазиоптимальные фильтры, амплитудно-частотная характеристика которых может иметь произвольную форму (ближе к прямоугольной). Эффективную полосу пропускания квазиоптимального фильтра выбирают такой, чтобы при данной форме его амплитудно-частотной характеристики обеспечивалось максимально возможное отношение сигнал/шум на выходе.

Для прямоугольного радиоимпульса максимум отношения сигнал / шум обеспечивается при ширине полосы пропускания квазиоптимального фильтра D fэф, равной:

- при использовании идеального полосового фильтра (с прямоугольной амплитудно-частотной характеристикой)

при этом ,

- при использовании одиночного параллельного колебательного контура

.

Энергетический проигрыш в отношении сигнал / шум при использовании вышеуказанных квазиоптимальных фильтров вместо оптимальных не превышает 18¸ 19 % .

При приёме непрерывной последовательности импульсов ширина полосы пропускания квазиоптимального фильтра должна быть примерно в два-три раза больше, чем для одиночного импульса. Это объясняется тем, что кроме флуктуационных помех на помехоустойчивость приёма последовательности импульсов оказывает влияние также и межсимвольная интерференция (взаимное наложение импульсов на выходе фильтра). В этом случае полосу пропускания выбирают из условия минимизации на выходе фильтра суммы флуктуационной помехи и межсимвольной интерференции.

2.9 Использование сложных сигналов для передачи

дискретных сообщений

Решение проблемы повышения помехозащищённости систем связи и управления достигается использованием различных методов и средств, в том числе и сигналов сложной формы (с большой базой).

Широкое практическое применение получили сложные сигналы на основе дискретных кодовых последовательностей, которые представляют собой последовательности символов di длительностью Т, принимающих одно из двух значений: +1 или –1. Такие сигналы легко формируются и обрабатываются с использованием элементов цифровой и вычислительной техники.

Сложные сигналы должны удовлетворять ряду требований для достижения наибольшей достоверности их приёма:

а) корреляционная функция должна содержать значительный максимум (пик);

б) взаимная корреляционная функция (ВКФ)

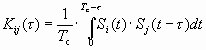(2.21)

любой пары сигналов из используемого ансамбля, определяющая степень их ортогональности, должна быть близка к нулю при любом t .

Однако на практике для реальных сигналов последнее условие не может быть выполнено. Поэтому для используемых сигналов важно обеспечить возможно большее отношение Kii(t ) / Kij(t ), оно и будет определять помехозащищённость приёма сигналов (например, для случая передачи двоичных сообщений это будут вероятности p(1/0) и p(0/1)).

Отличительная особенность ВКФ в том, что она не является чётной функцией аргумента t , т.е. Kuv (t ) ¹ Kuv (-t ) , а максимальный выброс достигается не обязательно при t =0.

Известно, что сигнал на выходе согласованного фильтра в произвольный момент времени характеризуется интегралом свёртки вида

,

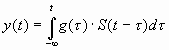где g(t ) – импульсная характеристика фильтра.

Выходной сигнал СФ совпадает по форме с функцией корреляции входного сигнала, т.е.

y(t) = a× Kss (t - t0), (2.22)

где a – множитель пропорциональности;

t0 – сдвиг в сторону запаздывания.

На практике величину t0 выбирают равной длительности сигнала,
т.е. t0 = Tс.

Для корреляционной функции дискретного сигнала общего вида применима формула

, (2.23)

здесь n указывает количество элементов, на которое осуществляется сдвиг исходного дискретного сигнала (n – целое число, положительное, отрицательное или нуль), так как важнейшей операцией при корреляционной обработке дискретных сигналов с использованием согласованного фильтра является поэлементный сдвиг такого сигнала.

Взаимная корреляционная функция двух дискретных сигналов по аналогии с корреляционной функцией одиночного сигнала определяется формулой

. (2.24)

Влияние помехи в линии связи на передаваемый сигнал будет проявляться в изменении знака (полярности) элемента дискретного сигнала, т. е. в переходах вида 1 ® - 1 и - 1 ® 1. При приёме с помощью согласованного фильтра это будет приводить к изменению формы сигнала на его выходе – уменьшению основного лепестка, увеличению боковых выбросов и, следовательно, к снижению помехоустойчивости приёма. Поэтому целесообразно выбрать оптимальную величину порога решающей схемы приёмника, минимизирующую среднюю вероятность ошибки. При равновероятной передаче сообщений оптимальный порог должен выбираться как среднее значение между уровнем основного лепестка и максимальным уровнем выброса ВКФ.

Согласованный фильтр для дискретных последовательностей может быть реализован в виде линии задержки с отводами (с общим временем задержки, равным длительности сигнала Тс ), фазовращателей (инверторов) в отводах и суммирующей схемы, на выходе которой возникает импульс, равный сумме амплитуд всех элементов сигнала.

Устройства, реализующие согласованную фильтрацию дискретных сигналов, могут быть выполнены также и на основе регистра сдвига с количеством разрядов, равным количеству элементов в кодовой последовательности сигнала. В соответствии с (2.23) и (2.24) должны быть перемножители и сумматоры. На вход перемножителей поступают принимаемая последовательность с разрядов регистра сдвига и опорная последовательность, совпадающая по виду с импульсной характеристикой входного сигнала с эталонного регистра. Сигналы с выходов всех разрядов перемножителей поступают на сумматор. Очевидно, что максимальный отклик на выходе сумматора будет наблюдаться тогда, когда кодовая последовательность полностью будет введена в регистр сдвига, т. е. в момент окончания входного сигнала.

Примечание: нетрудно видеть, что сигнал на выходе сумматора будет иметь вид ступенчатой функции. После сумматора может быть установлен интегратор, например, простейшая RC-цепочка для ’’сглаживания’’ сигнала.

Способ вычисления функции корреляции для заданных дискретных сигналов наглядно продемонстрирован в [5] (стр. 93 – 95, 100 – 101).

Проиллюстрируем нахождение корреляционной функции на примере ВКФ двух заданных сигналов из 5 элементов вида

u ={ 1, 1, 1, –1, –1} , v = { 1, –1, 1, –1, 1} .

Если n > 0, то сигнал v в (2.24) запаздывает относительно u, при n < 0 сигнал v сдвигается в сторону опережения. С учётом поэлементного сдвига последовательности v относительно последовательности u получим следующие результаты:

u. . . 0 0 0 0 0 +1 +1 +1 -1 -1 0 0 0 0 0 . . .

n = 0 v. . . 0 0 0 0 0 +1 -1 +1 -1 +1 0 0 0 0 0 . . .

Рез-т перемнож. = 1 -1 1 1 -1 Рез-т суммиров. Kuv (0) = 1.

u. . . 0 0 0 0 0 +1 +1 +1 -1 -1 0 0 0 0 0 . . .

n = 1 v(+1) . . 0 0 0 0 0 +1 -1 +1 -1 +1 0 0 0 0

Рез-т перемнож. = 0 1 -1 -1 1 0 Рез-т суммиров. Kuv (1) = 0.

u. . . 0 0 0 0 0 +1 +1 +1 -1 -1 0 0 0 0 0 . . .

n = 2 v(+2) . . 0 0 0 0 0 +1 -1 +1 -1 +1 0 0 0 0

Рез-т перемнож. = 0 0 1 1 -1 0 Рез-т суммиров. Kuv (2) = 1.

u. . . 0 0 0 0 0 +1 +1 +1 -1 -1 0 0 0 0 0 . . .

n = 3 v(+3) . . 0 0 0 0 0 +1 -1 +1 -1 +1 0 0 0

Рез-т перемнож. = 0 0 0 -1 1 0 Рез-т суммиров. Kuv (3) = 0.

u. . . 0 0 0 0 0 +1 +1 +1 -1 -1 0 0 0 0 0 . . .

n = 4 v(+4) . . 0 0 0 0 0 +1 -1 +1 -1 +1 0 0

Рез-т перемнож. = 0 0 0 0 -1 0 Рез-т суммиров. Kuv (4) = -1.

При n = 5 Kuv (5) = 0.

Аналогично составляем семейство последовательностей для n < 0 и находим Kuv (- n). Получим

Kuv (-1) = -2, Kuv (-2) = 1, Kuv (-3) = 0, Kuv (-4) = 1, Kuv (-5) = 0.

Согласованный фильтр обеспечивает при флуктуационной помехе в канале типа “ белого шума “ в момент окончания сигнала t0 = Тс на своём выходе максимально возможное отношение пиковой мощности сигнала к мощности помехи. Выигрыш в отношении сигнал / шум на выходе СФ по сравнению со входом равняется базе сигнала (В = 2· Fс· Тс), т. е.

, (2.25)

где Тс = N× Т – длительность сигнала (N - число элементов в дискретной последовательности);

– ширина спектра сигнала.

Таким образом, выигрыш q = (hвых)2 / (hвх)2, обеспечиваемый СФ при приёме дискретных последовательностей, составляет N раз. Следовательно, путём увеличения длины дискретных последовательностей, отображающих символы сообщений ² 1² и ² 0² , можно обеспечить значительное повышение отношения сигнал / шум на входе решающей схемы приёмника и, соответственно, повышение помехоустойчивости (достоверности) передачи дискретных сообщений. Очевидно, что это будет приводить к снижению скорости передачи сообщений, то есть реализуется принцип обмена скорости передачи дискретных сообщений на помехоустойчивость их приёма путём увеличения энергии элемента сигнала Eс = PсT.

назад | оглавление | вперёд