| Цифровая обработка сигналов |
| Учебное пособие по курсу “Цифровая обработка сигналов” |
назад | оглавление | вперёд |
Учебное пособие по курсу
“Цифровая обработка сигналов”
часть II
1. Цифровые фильтры. Общая характеристика.
В цифровой вычислительной системе, предназначенной для обработки сигналов действие над отсчетами сигнала, заменяется действием над кодовыми словами. Структурная схема подобного цифрового фильтра представлена на рис. 1.

Рисунок 1.
Где ЭК - электронный ключ. Производит преобразование аналогового сигнала в отсчеты. На выходе последовательность АИМ-1.
АЦП - аналого-цифровой преобразователь. На выходе вместо отсчетов сигнала появляются кодовые слова, т.е. АИМ-2.
ЦФ - осуществляет операцию над кодовыми словами в соответствии с заданным алгоритмом (например, в соответствии с заданным разностным уравнением).
ЦАП - цифро-аналоговый преобразователь. На его выходе вместо кодовых слов появляются отсчеты выходного сигнала.
АСФ - аналоговый синтезирующий фильтр (ФНЧ). На его выходе появляется выходной аналоговый сигнал.
На рис. 2 показаны качественно происходящие процессы в отдельных
узлах при цифровой обработке сигналов. Так под цифрой 1 показан входной аналоговый
сигнал X(t), под цифрой 2 - отсчеты аналогового сигнала Х(пТ), под цифрой
3 - выходной сигнал цифрового фильтра, под цифрой 4 - огибающая цифрового
сигнала.
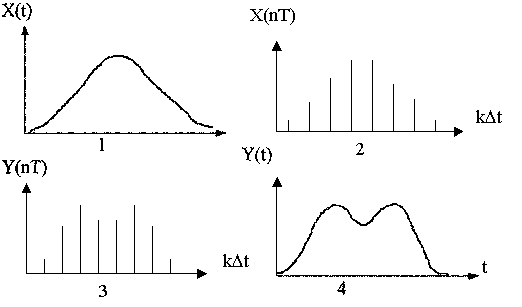
Рисунок 2.
Применение цифровых фильтров позволяет получать высокое качество обработки сигналов. Поскольку кодовые слова Х(nТ) и Y(nT) имеют конечную длину, то сигнал на выходе Y(t) будет отличаться от идеального варианта обработки на некоторую величину. Здесь сказывается эффект конечной разрядности. Эти эффекты учитываются в окончательной схеме цифрового фильтра и рассматриваются ниже.
2. Структура и основные характеристики цифрового фильтра
Любую RLC цепь можно описать дифференциальными уравнениями. При переходе от непрерывных сигналов к дискретным дифференциальное уравнение заменяется разностным уравнением. А разностному уравнению соответствует цепь, элементы которой принципиально отличаются от элементов RLC. Такое разностное уравнение общего вида, связывающее сигнал на входе и выходе дискретной цепи имеет вид:
 (1)
(1)
где Х(nТ) сигнал на входе,
Y(nT) - сигнал на выходе,
М - число прямых связей системы,
L - число обратных связей системы,
m, е - целые числа (1, 2, 3 ...)
Этому разностному уравнению соответствует дискретная цепь (рис. 3).
Рисунок 2.
На этой схеме![]() соответствует элемент
задержки на время Т (Т - шаг дискретизации). Элемент
соответствует элемент
задержки на время Т (Т - шаг дискретизации). Элемент ![]() означает умножитель
на величину ai или bi. Элемент
означает умножитель
на величину ai или bi. Элемент ![]() означает сумматор.
означает сумматор.
Методы решения разностных уравнений имеют много общего с методами решений дифференциальных уравнений и позволяют получить решение в общем виде. Мы ограничимся численными методами решения. Разностное уравнение является алгоритмом работы дискретной системы. Такая цепь реализуется либо в виде программы работы на ЭВМ, либо в виде специализированного вычислителя.
Пример №1.
Составить структурную схему по следующему разностному уравнению:
Y(nT) = 0,4Х(пТ) - 0,2Y(nT - Т) + 0,3Y(nT - 2Т) (2)
Решение: Данному разностному уравнению соответствует структурная схема,
изображенная на рис. 4.
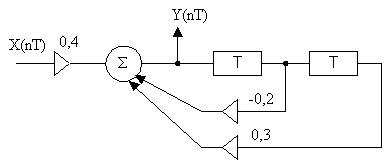
Рисунок 4.
Пример №2.
Составить разностное уравнение по заданной структурной схеме (рис.5) и решить его для заданной последовательности Х(пТ)={1,0; 0,5;0}
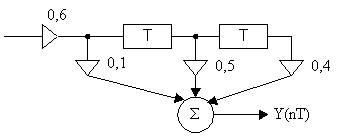
Рисунок 5.
Решение: Данной структурной схеме соответствует разностное уравнение
Y(nT) = 0,6[0,1Х(nТ) + 0.5Х(nТ - Т) + 0,4Х(nТ - 2Т)]
Найдем решение данного уравнения численными методами
n = 0 → Y(OT) = 0,6*0,1Х(0Т) = 0,06
n = 1 → Y(1T) = 0,6[0,1Х(1Т) + 0,5Х(1Т - Т)]= 0,6*0,1*0,5 + 0,6*0,5*1=0,45
n = 2 → Y(2T) = 0,6[0,1Х(2Т) + 0,5Х(2Т - Т) + 0,4Х(2Т - 2Т)] =
= 0,6[0,1*0 + 0,5*0,5 + 0,4*1] = 0,39
Y(nT)= {0,06; 0,45; 0,39}
Наряду с разностным уравнением очень часто структуру цифрового фильтра характеризуют передаточной характеристикой. Если разностное уравнение характеризует заданную цепь во временной области, то переда-
точная характеристика характеризует эту же цепь в частотной области. Численное выражение для передаточной характеристики равно:
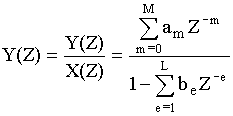 (3)
(3)
В выражении (3) Y(Z) – Z - преобразование выходного сигнала.
X(Z) – Z - преобразование входного сигнала. Z = е -j2π/N: Т - период дискретизации, w - круговая частота, am - коэффициенты передачи нерекурсивной цепи, be - коэффициенты передачи рекурсивной цепи, Z-1 - характеризует задержку сигнала не один тактовый интервал, М, L - соответственно характеризует количество прямых и обратных связей системы.
Если 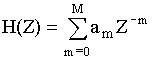 , то цепь называется нерекурсивной.
, то цепь называется нерекурсивной.
Если 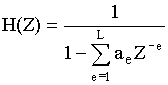 - то цепь рекурсивная.
- то цепь рекурсивная.
Пример №3.
Пользуясь рис. 4 и рис. 5, составить уравнения для передаточной характеристики.
Решение: Цифровой фильтр, изображенный на рис. 4, характеризуется следующим видом H(Z)
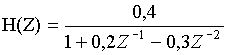 (4)
(4)
а изображенный на рис. 5 характеризуется как
H(Z) =0,6 [0,1 + 0,5Z-1 + 0,4Z-2] (5)
При анализе работы любой цифровой структуры важное место приобретает вопрос устойчивости. Если по каким-то причинам цепь оказывается неустойчивой, то вместо желаемого фильтра получают генератор. Критерий устойчивости дискретной цепи можно получить, зная критерий устойчивости непрерывной цепи. Дискретная цепь будет устойчива, если полюсы Н(Р) расположены в левой полуплоскости комплексной переменной Р = δ + jw. При переходе к плоскости Z левая плоскость комплексной переменной отображается на внутреннюю часть единичного круга Z. Следовательно, полюсы H(Z) дискретной цепи должны располагаться внутри единичного круга плоскости Z. Это и есть принцип устойчивости.
Пример №4.
Дискретная цепь описывается передаточной функцией
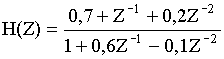 (6)
(6)
Определить устойчивость данной цепи.
Решение. Для решения данной задачи преобразуем H(Z) к следующему виду
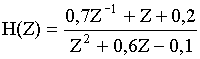 (7)
(7)
Приравняем знаменатель (Z) к нулю и найдем корни
Z2 + 0,6Z - 0,1 = 0; 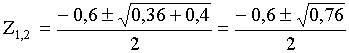
![]()
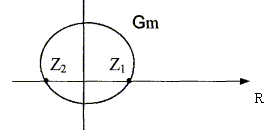
Рисунок 6.
Так как оба корня находятся внутри единичного круга Z плоскости, то цепь с передаточной характеристикой (6) является устойчивой. В некоторых случаях дискретная цепь оказывается неустойчивой. Однако такую цепь можно также реализовать, перейдя от рекурсивной цепи к нерекурсивной цепи.
Пример №5.
Определить устойчивость цепи
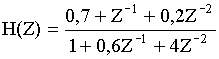 (8)
(8)
В случае обнаружения неустойчивости произвести преобразование рекурсивной цепи в нерекурсивную цепь.
Решение: Воспользовавшись приемом в примере 4, находим, что:
Z1 = l,65; Z2 = -2,25
Цепь, характеризуемая выражением (8) неустойчива. Произведем преобразование. Для этого выражение (8) представим к виду:
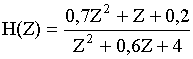
Поделим числитель на знаменатель. Дискретная цепь, характеризуемая H(Z) выражением (8), реализуема и устойчива с передаточной характеристикой.
H(Z) = 0,7Z - 0.4Z-1 - 0,08Z-2...
Наряду с характеристикой H(Z) очень часто дискретную цепь характеризует так называемой импульсной реакцией h(nT). Импульсной реакцией цепи h(nT) называется отклик цепи на единичную δ функцию. Если H(Z) характеризует систему в частотной области, то h(nT) как и разностное уравнение характеризует цепь во временной области. Обе характеристики связаны с Z преобразованием. Определить h(nT) можно различными методами:
1. По известному разностному уравнению, если Х(nТ) = {1; 0}, тогда у(пТ) будет искомой h(nT), т.е. y(nT) = h(nT),
2. По известному H(Z), используя формулу обратного Z преобразования или теорему разложения,
3. Численными методами, применяя деление полинома числителя на полином знаменателя. Использование этого приема показано в примере №5.
Расчет X(jkw1), H(jkw1) и у(nТ) с применением БПФ и ОБПФ.
Связь между отсчетами во временной и частотной областях устанавливается формулами ДПФ.
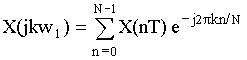 – ДПФ
– ДПФ
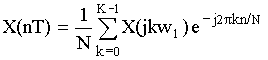 – ОДПФ
– ОДПФ
где 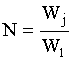 – количество отсчетов во временной и частотной
областях.
– количество отсчетов во временной и частотной
областях.
Оба преобразователя можно вычислить с помощью одного и того же алгоритма. Для этого используют выражение:
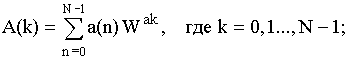
W = ej2 – весовая функция.
Для прямого ДПФ a(n) =X(nT), aX(jkw1) = A(k).
При вычислении ОДПФ а(n) = X(jW1(N-n)), где n = 1, 2 ... N-1; а(0) = Х(0);
а ![]()
Анализ алгоритма ДПФ показывает, что количество операций умножения будет равно N2. Этот алгоритм содержит большое количество избыточных операций, в том числе и таких, когда одни и те же операции многократно выполняются над одними и теми же значениями величин. Устранение избыточных операций умножения приводит к алгоритму быстрых преобразований Фурье. На рис. 7 приведена схема восьмиточечного БПФ.
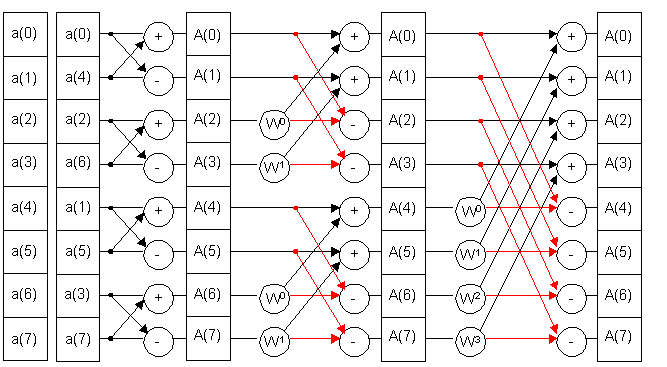
Рисунок 7.
При БПФ исходные отсчеты подаются на входы преобразователя не в естественном порядке. Для получения номеров отсчетов в требуемой последовательности необходимо номера отсчетов исходной последовательности представить в двоичной системе счисления, а затем для каждого номера переставить разряды, записав их в обратном порядке (таб.1).
Таблица 1.
| 0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Естественный порядок |
| 000 |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
|
| 000 |
100 |
010 |
110 |
001 |
101 |
011 |
111 |
Двоично-инверсный порядок |
| 0 |
4 |
2 |
6 |
1 |
5 |
3 |
7. |
На рис. 8 изображена схема алгоритма перестановки. Здесь N - количество элементов исходной последовательности, A(i) - ячейки для хранения данных исходной последовательности.
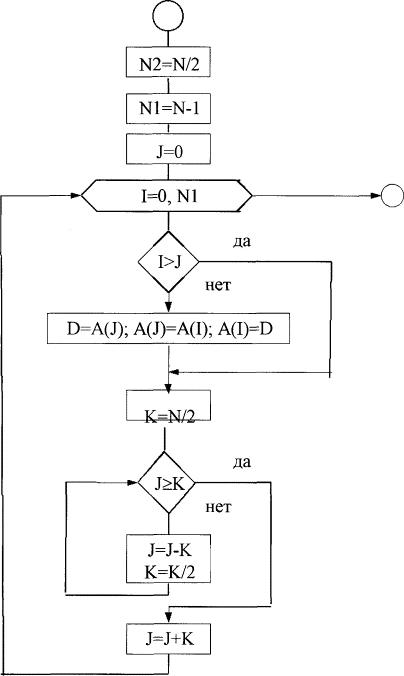
Рисунок 8.
Согласно этого алгоритма перестановка осуществляется непосредственно над содержимым ячеек, хранящих данные исходной последовательности. При этом получение двоично-инверсной последовательности не требует использования дополнительного массива ячеек памяти. Она формируется в том же массиве ячеек, в котором хранилась исходная последовательность. На рис. 9 показана схема алгоритма БПФ.
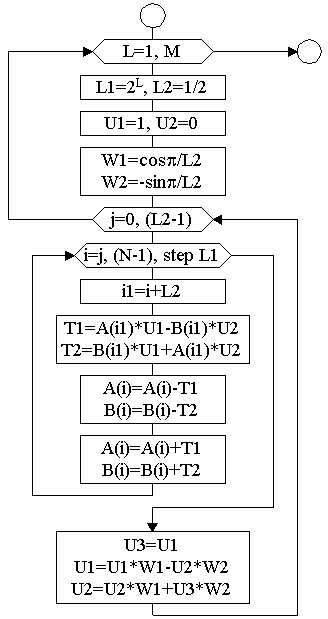
Рисунок 9.
В этом алгоритме:
М = log2N - количество этапов БПФ,
N - количество элементов исходной последовательности,
L1 - определяет количество взаимодействующих элементов входной последовательности на каждом этапе БПФ (на первом этапе - 2, на втором- 4 и т.д.),
L2 - количество весовых функций, вычисляемых на каждом этапе преобразования (на первом этапе - 1(W0); на втором - 2(W0, W1); на
третьем - 4(W0, W1, W2, W3) и т.д.).
Весовая функция Wnk= (e-2π/N)nk представлена по формуле Эйлера;
![]()
A(i), B(i) - действительная и мнимая составляющие гармоники БПФ. Переменные i и il определяют взаимодействующие пары А(р) и А(g), согласно схеме на рис. 10.
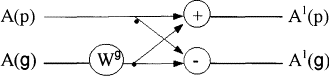
Рисунок 10.
В процессе выполнения алгоритма БПФ на любом его этапе
результат вычисления соответствующих пар значений А1(р),
A1(g) (рис. 9)
получаются путем взаимодействия только А(р) и А(g), которые берутся из результата
предыдущего этапа БПФ. Вычисленные значения А1 (р), А1(g)
помещаются в ячейки, хранящие результаты предыдущего этапа. Т.о. обобщенный
алгоритм БПФ имеет вид, представленный на рис. 11.

Рисунок 11.
При ОБПФ может быть использован алгоритм
БПФ, но при вводе массива исходной последовательности необходимо предусмотреть
ячейки для записи вещественной и мнимой составляющих X(jkw1).
Весовая функция при этом ![]()
т.е. W1 = cos(π/L2), W2 = sin(π/L2) (рис. 9).
Полученные в результате вычислений ОБПФ значения Х(nТ) должны быть разделены на N. В курсовой работе по приведенному алгоритму необходимо составить программу БПФ и ОБПФ на языке высокого уровня. При расчете X(jkWl), исходной последовательностью является входное воздействие Х(nТ), при расчете H(jkWl) - импульсная реакция h(nT), определяемая по передаточной характеристике H(Z). Выходной сигнал у(пТ) может быть определен двумя путями:
1. С применением круговой свертки во временной области
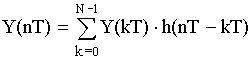
2. С применением расчетов в частной области. По рассчитанным X(jkWl) и H(jkWl) определяют Y(jkWl), а затем, применяя ОБПФ, находят у(nТ).
3. Реализация H(Z) на МПК 1813ВЕ1
Для процессоров фильтрации или коррекции сигналов в диапазоне частот канала ТЧ, требуется быстродействующее МПК. Одним из них является ВМ1813ВЕ1, позволяющий в реальном масштабе времени создать до пяти фильтров восьмого порядка. МПК 1813ВЕ1 оперирует с аналоговыми и цифровыми сигналами, при этом аналоговая и цифровая части его работают параллельно.
В таблице 2 приведены команды, выполняемые в цифровой части, а в таблице 3 - в аналоговой части МПК 1813ВЕ1.
Для обеспечения синхронной работы цифровой и аналоговой частей МПК используются пустые команды:
• в цифровой части - пустые пересылки (LDA),
• в аналоговой - команда NOP.
Рассмотрим пример реализации на ВМ 1813ВЕ1 цифрового фильтра второго порядка, передаточная функция которого имеет вид:
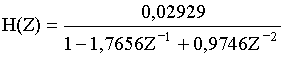
Прейдем к разностному уравнению:
Y(kT) = 0,02929X(kT) + l,7656Y(kT - Т) - 0,9746Y(kT - 2Т)
Введем обозначения:
Y0 = y(kT)
Х = x(kT)
Yl = y(kT - T)
Y2 = y(kT - 2T)
Таблица 2.
| №п/п |
Мнемоника |
Двоичный код |
Комментарии |
| 1 2 3 4 5 6 7
8 |
ADD SUB LDA XQR ABA ABS LIM
AND |
110 101 111 000 100 011 010
001 |
В + 2n·А→В В – 2n·А→В А·2n→В ВÅ(2n·А) →В В·|2n·А|→В |2n·А|→В +1→В, если А>0 -1→В, если А<0 В·(А·2n) →В |
| При организации условных переходов |
|||
| 9
10
11
12 13 |
ADD CND(k)
SUB CND(k)
LDA CND(k)
ABA CND(k) XQR CND(k) |
110
101
111
100 000 |
В+(2n·А)→В,если DAR(k)=1;k=0,1... 8 В→В, если DAR(k)=0 B·(A·2n)→B, если DAR(k)=l В+(А·2n)→В, если DAR(k)=0 А·2n→В, если DAR(k)=l В→В, если DAR(k)=0 |(A·2n)|(mod2)B→B (А·2n) + В→В |
Здесь (mod 2) - операция сложения по модулю 2.
Таблица 3.
| № п/п |
Мнемоника |
Код операции |
Комментарии |
|
| ADF |
ADK |
|
||
| 1. |
IN(k) k=0¸3 |
00 00 00 00 |
000 001 010 011 |
Ввод сигнала по 1 каналу Ввод сигнала по 2 каналу Ввод сигнала по 3 каналу Ввод сигнала по 4 каналу |
| 2. |
NOP |
00 |
100 |
Отсутствие операций |
| 3. |
EOP |
00 |
101 |
Возврат работы ПЗУ к нулевой ячейке |
| 4. |
CUTS |
00 |
110 |
Формирование в АЦП знакового разряда |
| 5. |
CUT(k) |
10 ... 10 |
000 … 111 |
Преобразование младшего разряда
Преобразование старшего (8-го) разряда |
| 6. |
CNDS |
00 |
111 |
Условная операция по знаковому разряду |
| 7. |
OUT(k) k=0¸7 |
01 … 01 |
000 … 111 |
Вывод сигнала по 1 каналу
Вывод сигнала по 8 каналу |
| 8. |
CND(k) |
11 … 11 |
000 … 111 |
Условная операция по младшему разряду DAR Условная операция по старшему разряду DAR |
Для уменьшения времени при выполнении операций умножений, представим коэффициенты в следующем виде:
0,02929 » 2-8 – 2-10
1,7656 » 21-2-2+2-6
-0,9746 » -20+2-7-2-9
В этом случае, для того, чтобы умножить X(kT) на соответствующий коэффициент (0,02929), достаточно сделать сдвиг вправо X(kT) на 8 и на 10 разрядов. Полученные величины вычесть друг из друга, т.е.
0,02929X(kT) = Х*2-8 - Х*2-10
В таблице 4 приведена программа реализации фильтра.
Таблица 4.
| № п/п |
КОП цифровой |
Код операнда В |
Код операнда A |
Код. масшт. устройства |
КОП аналого- вый |
Комментарии |
|
| 1 |
LDA |
Y2 |
Yl |
R00 |
IN(0) |
Y2=Y1 В аналоговой части осуществляется ввод сигнала по "Æ" ка-налу. Команда ввода повторяется 8 раз подряд. |
|
| 2 |
LDA |
Yl |
Y0 |
R00 |
IN(0) |
Y1=Y0 |
|
| 3 |
LDA |
Y0 |
Yl |
L02 |
IN(0) |
Y0=Ylx21 |
|
| 4 |
SUB |
Y0 |
Yl |
R02 |
IN(0) |
Y0=Y0-2-2xYl |
|
| 5 |
ADD |
Y0 |
Yl |
R06 |
IN(0) |
Y0=Y0+26xYl |
|
| 6 |
SUB |
Y0 |
Y2 |
L01 |
IN(0) |
Y0=Y0-2 xY2 |
|
| 7 |
ADD |
Y0 |
Y2 |
R07 |
IN(0) |
Y0=Y0+2-7xY2 |
|
| 8 |
SUB |
Y0 |
Y2 |
R09 |
IN(0) |
Y0=Y0-2-9xY2 |
|
| 9 |
LDA |
Y0 |
Y0 |
R00 |
CUTS |
В цифровой части холост, операция. В аналоговой части преобр.знака |
|
| 10 |
LDA |
Y0 |
Y0 |
R00 |
NOP |
холостые |
|
| 11 |
LDA |
Y0 |
Y0 |
R00 |
NOP |
операции |
|
| 12 |
LDA |
Y0 |
Y0 |
R00 |
CUT(7) |
Преобразование 7 разряда мантиссы |
|
| 13 |
LDA |
Y0 |
Y0 |
R00 |
NOP |
холостые |
|
| 14 |
LDA |
Y0 |
Y0 |
R00 |
NOP |
операции |
|
| 15 |
LDA |
Y0 |
Y0 |
R00 |
CUT(7) |
Преобразование 6 разряда мантиссы |
|
| 16 |
LDA |
Y0 |
Y0 |
R00 |
NOP |
|
|
| 17 … |
LDA |
Y0 |
Y0 |
R00 |
NOP |
|
|
| 35 |
LDA |
Y0 |
Y0 |
R00 |
CUT(O) |
Преобразование младш. разряда мантиссы |
|
| 36 |
LDA |
Y0 |
Y0 |
R00 |
NOP |
|
|
| 37 |
LDA |
Y0 |
Y0 |
R00 |
NOP |
|
|
| 38 |
ADD |
X |
DAR |
R00 |
NOP |
X=DAR |
|
| 39 |
SUB |
Y0 |
X |
R08 |
NOP |
Y0=Y0+2-8 |
|
| 40 |
LDA |
Y0 |
X |
R10 |
NOP |
Y0=Y0-2-l0xX |
|
| 41 |
LDA |
DAR |
Y0 |
|
NOP |
DAR=Y0 |
|
| 42 … |
LDA |
Y0 |
Y0 |
R00 |
OUT(l) |
Вывод по первому выходу (повторяет-ся 8 раз подряд) |
|
| 49 |
LDA |
Y0 |
Y0 |
R00 |
OUT(l) |
|
|
| 50 |
LDA |
Y0 |
Y0 |
R00 |
EOP |
Возврат в начало программы |
|
Программа начинается с переприсвоения переменных, что эквивалентно сдвигу выходного сигнала в первой и второй линиях задержки. Процесс умножения на заданные коэффициенты производится путем сдвигов вправо или влево операнда А в масштабирующем устройстве. При сдвиге вправо используется мнемоническое обозначение R, а влево - L. Время, отводимое на выполнение всей программы, составит:
600нс*52=31мкс.
назад | оглавление | вперёд