|
Математическая
теория сигналов
|
3.1 Дискретизация во времени
Преобразование
непрерывного аналогового сигнала в дискретный может быть осуществлено в
соответствии с теоремой отсчетов, доказанной В.А. Котельниковым в 1933 г.:
любой непрерывный
сигнал с ограниченным частотой FМАКС спектром, может быть полностью представлен
в виде своих дискретных во времени отсчетов, взятых через интервал времени
Тд  1/2 Fмакс,
называемой периодом дискретизации. Технически операция дискретизации
по времени осуществляется при помощи ключевых схем путем получения сигналов
с амплитудно-импульсной модуляцией (АИМ). При АИМ амплитуда периодической
последовательности импульсов изменяется в соответствии с изменением амплитуды
модулирующего сигнала с(t) (например, телефонного сигнала). Различают
амплитудно-импульсную
модуляцию первого (АИМ-1) и второго (АИМ-2) рода. При АИМ-1 амплитуда
отсчетов, следующих с частотой дискретизации
1/2 Fмакс,
называемой периодом дискретизации. Технически операция дискретизации
по времени осуществляется при помощи ключевых схем путем получения сигналов
с амплитудно-импульсной модуляцией (АИМ). При АИМ амплитуда периодической
последовательности импульсов изменяется в соответствии с изменением амплитуды
модулирующего сигнала с(t) (например, телефонного сигнала). Различают
амплитудно-импульсную
модуляцию первого (АИМ-1) и второго (АИМ-2) рода. При АИМ-1 амплитуда
отсчетов, следующих с частотой дискретизации , изменяется в соответствии с изменением
модулирующего сигнала с(t) на интервале времени передачи отсчета (и, а
при АИМ-2 амплитуда каждого отсчета постоянна и равна значению модулирующего
сигнала в начальный момент отсчета. На рисунке 3.1 представлен исходный
модулирующий
сигнал с(t), а также сигналы АИМ-1 и АИМ-2 в случае дискретизации двухуровневых
сигналов.Сигналы АИМ-1 и АИМ-2 в общем случае имеют различную форму, а значит их частотные спектры G1(f) и G2(f), определяемые преобразованием Фурье:
, изменяется в соответствии с изменением
модулирующего сигнала с(t) на интервале времени передачи отсчета (и, а
при АИМ-2 амплитуда каждого отсчета постоянна и равна значению модулирующего
сигнала в начальный момент отсчета. На рисунке 3.1 представлен исходный
модулирующий
сигнал с(t), а также сигналы АИМ-1 и АИМ-2 в случае дискретизации двухуровневых
сигналов.Сигналы АИМ-1 и АИМ-2 в общем случае имеют различную форму, а значит их частотные спектры G1(f) и G2(f), определяемые преобразованием Фурье:


Рисунок 3.1 - Формирование
АИМ сигнала.
также
имеют разный вид. Однако, если длительность АИМ отсчетов (и много меньше
периода дискретизации Тд >> и ,
т.е. скважность импульсной последовательности разница между сигналами АИМ-1
и АИМ-2 оказывается несущественной,
а их
частотные спектры практически совпадают: G1(f) = G2(f)
= G(f). Это условие выполняется
в ЦСП, так как длительность канальных импульсов (и выбирается из условия
где
и ,
т.е. скважность импульсной последовательности разница между сигналами АИМ-1
и АИМ-2 оказывается несущественной,
а их
частотные спектры практически совпадают: G1(f) = G2(f)
= G(f). Это условие выполняется
в ЦСП, так как длительность канальных импульсов (и выбирается из условия
где  и=Tи/N,
N - число каналов.Легко показать, что при
T
и=Tи/N,
N - число каналов.Легко показать, что при
T 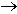
 (идеальной дискретизации) сигналы FАИМ-1(t) = FАИМ-2(t)
= Fид(t) и имеют вид
(идеальной дискретизации) сигналы FАИМ-1(t) = FАИМ-2(t)
= Fид(t) и имеют вид
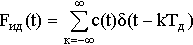
а частотный спектр определяется следующим образом:
где G(f) спектр исходного сигнала ограниченный минимальной (FМИН) и максимальной (FМАКС) частотами.Вид частотного спектра
G(f) для АИМ сигнала при Тд >> ( приведен на рисунке 3.2.
( приведен на рисунке 3.2.
Рисунок
3.2 - Спектральный состав АИМ сигнала.
Частотный спектр модулированной последовательности при АИМ содержит:
- постоянную
составляющую G0;
- составляющие
с частотами исходного сигнала FМИН
 FМАКС;
FМАКС;
- составляющие
с частотой дискретизации Fд и ее гармоник к Fд;
- составляющие
боковых полос (верхней и нижней) при частоте дискретизации
Fд и ее гармоник
к Fд  (FМИН
(FМИН FМАКС).
FМАКС).
При дискретизации двух полярных сигналов (телефонных, звукового вещания) в спектре АИМ сигнала практически отсутствуют постоянная составляющая и ее гармоники.Из рисунка
3.2 видно, что для восстановления исходного непрерывного сигнала из АИМ сигнала,
на приеме
достаточно поставить
ФНЧ (или фильтр-интерполятор) с частотой среза, равной FМАКС,
который выделит исходный сигнал. Поскольку при организации телефонного
канала FМАКС = 3,4
кГц, то Fд должна выбираться из условия Fд 6,8
кГц. Реально, при построении ЦСП с ИКМ выбрана Fд = 8 кГц, что
позволяет упрощать требования к ФНЧ приема.
При Fд = 8 кГц полоса расфильтровки
6,8
кГц. Реально, при построении ЦСП с ИКМ выбрана Fд = 8 кГц, что
позволяет упрощать требования к ФНЧ приема.
При Fд = 8 кГц полоса расфильтровки  Fр оказывается достаточно
большой, составляет
Fр оказывается достаточно
большой, составляет
 Fр = (Fд - FМАКС) - FМАКС = 1,2 кГц
Fр = (Fд - FМАКС) - FМАКС = 1,2 кГц
и позволяет достаточно просто реализовывать канальные фильтры-интерполяторы. Кроме того, выбор Fд = 8 кГц обусловлен тем, что эта частота кратна 2, что позволяет существенно упростить оборудование ЦСП с ИКМ, передающих цифровые сигналы на основе двоичной системы счисления.Анализ спектрального состава АИМ сигнала, приведенного на рисунке 3.2, позволяет подтвердить правильность выводов теоремы отсчетов. Как видно из рисунка 3.2, для того, чтобы не возникло необратимых частотных искажений, в спектр непрерывного сигнала не должны попадать частотные составляющие нижней боковой полосы частот при Fд, то есть:

Итак, при выполнении операции дискретизации во времени необходимо правильно выбрать частоту дискретизации, которая определяется параметром FМАКС непрерывного сигнала: Fд  2FМАКС. При передаче телефонных сигналов частота дискретизации стандартизирована во всем мире и равна Fд = 8 кГц.
2FМАКС. При передаче телефонных сигналов частота дискретизации стандартизирована во всем мире и равна Fд = 8 кГц.
Выводы по разделу
Преобразование непрерывного аналогового сигнала в дискретный может быть осуществлено в соответствии с теоремой отсчётов, доказанной В.А. Котельниковым. Дискретизация по времени осуществляется путём получения сигналов с амплитудно-импульсной модуляцией (АИМ). АИМ различают первого (АИМ-1) и второго (АИМ-2) рода.При выполнении операции дискретизации во времени необходимо правильно выбрать частоту дискретизации, которая определяется параметром FМАКС непрерывного сигнала: FД  FМАКС. При передаче телефонных сигналов частота дискретизации стандартизирована во всём мире и равна FД = 8 кГц.
FМАКС. При передаче телефонных сигналов частота дискретизации стандартизирована во всём мире и равна FД = 8 кГц.
3.2 Квантование по уровню
Как видно из рисунка 3.2, АИМ-сигнал является дискретным во времени, но непрерывным по уровню, так как амплитуда отсчетов может принимать бесконечное множество значений. Однако любая аппаратура обработки сообщений и систем передачи имеет конечную разрешающую способность. Это связано как с ошибками, возникающими при обработке сигналов, так и с наличием шумов и искажений в аппаратуре и каналах передачи.В
связи с этим нет необходимости передавать все бесконечное множество амплитудных
значений непрерывных сигналов,
его можно ограничить конечным множеством, содержащим определенное, заранее
установленное, для того или иного вида сигналов, число "разрешенных" амплитудных значений. Эти "разрешенные" для
передачи амплитудные значения сигнала называются уровнями квантования;
выбор их количества определяет качество передачи сигналов.При квантовании
по уровню весь возможный динамический диапазон сигнала от Uмакс до
Uмин разбивается
на разрешенные
уровни (если электрический сигнал передается в виде АИМ напряжения непрерывного
сигнала: F(t) = U(t). Разность между двумя соседними разрешенными для
передачи уровнями называется шагом квантования  .
Если амплитуда отсчета сигнала UАИМ(t)
в пределах двух соседних разрешенных значений превышает половину шага квантования
.
Если амплитуда отсчета сигнала UАИМ(t)
в пределах двух соседних разрешенных значений превышает половину шага квантования
 /2, ее значение увеличивается в большую сторону, если меньше половины
шага квантования - в меньшую сторону. Таким образом получается сигнал квантованный
по уровню - UКВ(t).
/2, ее значение увеличивается в большую сторону, если меньше половины
шага квантования - в меньшую сторону. Таким образом получается сигнал квантованный
по уровню - UКВ(t).
Разность
между истинным значением отсчета и его квантованным значением называется
ошибкой, или шумом квантования,
который определяется как 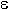 Ш КВ(t) =
UАИМ(t) - UКВ(t),
при этом |
Ш КВ(t) =
UАИМ(t) - UКВ(t),
при этом | Ш КВ (t)|
Ш КВ (t)| 
 /2
/2
Произведя "нумерацию" уровней
квантования можно передавать не сами уровни, а их значения по шкале уровней
в двоичном
коде. В этом случае на приеме восстановить квантованный по уровню сигнал
достаточно просто:
UКВ(t)пр
= li
Формула
3.1а
где li
= (0, lМАКС)
- номер разрешенного уровня в десятичной системе счисления;
 - шаг
квантования;
- шаг
квантования;
lМАКС -
максимально возможный уровень квантования, который определяется из условия:
UКВ(t)МАКС= lМАКС
формула
3.1б
Указанные выше преобразования иллюстрируются рисунком 3.3.Выбор шага
квантования  и количество уровней квантования lМАКС определяются, во-первых
параметрами преобразуемого
сигнала, в частности величиной UМАКС, а во-вторых допустимой
величиной помех, возникающих в канале, поскольку ошибки квантования при
передаче, например,
телефонного сигнала воспринимаются как специфический шум квантования, имеющий
некоторую мощность РШ КВ.Энергетический
спектр шумов квантования аналогичен энергетическому спектру "белого шума" и
имеет равномерный
характер в диапазонечастот:
-
и количество уровней квантования lМАКС определяются, во-первых
параметрами преобразуемого
сигнала, в частности величиной UМАКС, а во-вторых допустимой
величиной помех, возникающих в канале, поскольку ошибки квантования при
передаче, например,
телефонного сигнала воспринимаются как специфический шум квантования, имеющий
некоторую мощность РШ КВ.Энергетический
спектр шумов квантования аналогичен энергетическому спектру "белого шума" и
имеет равномерный
характер в диапазонечастот:
- < f <
< f < .Плотность
распределения вероятности W(x) шума квантования в пределах одного шага квантования
в интервале от -
.Плотность
распределения вероятности W(x) шума квантования в пределах одного шага квантования
в интервале от -  /2 до
/2 до  /2,
также имеет равномерный вид и показана на рисунке 3.4.
/2,
также имеет равномерный вид и показана на рисунке 3.4.

Рисунок
3.3 - Принципы квантования по уровню и формирования канального сигнала с
ИКМ.

Рисунок
- 3.4 Плотность распределения вероятности шума квантования.
Средняя
мощность случайного процесса с нулевым средним значением и одномерной плотностью
распределения вероятности (каковым является шум квантования), определяется
следующим образом:

Формула 3.2
где UKi
= li  - значение
i-го уровня квантования;
- значение
i-го уровня квантования;
x -
случайная величина погрешности
квантования;
 -
шаг квантования.
-
шаг квантования.
Так как погрешность квантования внутри каждого шага квантования имеет равномерный характер (рисунок 3.3) можно для простоты принять UKi = 0 и получить (из 3.2) выражение:

Формула 3.3
Мощность шума квантования не должна превышать допустимую норму на помехи на выходе канала, предназначенного для передачи различных аналоговых сигналов. Поскольку системы передачи с ИКМ плезиохронной цифровой иерархии (PDH) разрабатывались для передачи телефонных сообщений, далее определим минимально необходимое число уровней квантования при организации телефонного канала в ЦПС с ИКМ.Известно,
что согласно требованиям МСЭ-Т [8,9] суммарная допустимая мощность помех
Р на выходе канала тональной
частоты (ТЧ) эталонной цепи в точке нулевого относительного уровня (ТНОУ)
в час наибольшей нагрузки (ЧНН) не должна превышать величины Р
на выходе канала тональной
частоты (ТЧ) эталонной цепи в точке нулевого относительного уровня (ТНОУ)
в час наибольшей нагрузки (ЧНН) не должна превышать величины Р
 10000
пВт псоф. В канале ТЧ ЦСП с ИКМ величина помехи определяется только шумом
квантования (при отсутствии ошибок при передаче двоичных символов по линейному
тракту): РШ КВдоп = Р
10000
пВт псоф. В канале ТЧ ЦСП с ИКМ величина помехи определяется только шумом
квантования (при отсутствии ошибок при передаче двоичных символов по линейному
тракту): РШ КВдоп = Р = 10000 пВт псоф.При этом эффективное значение мощности шума квантования будет равно:
= 10000 пВт псоф.При этом эффективное значение мощности шума квантования будет равно:

где КПС = 0,75 псофометрический коэффициент, учитывающий чувствительность человеческого уха к различным частотным составляющим помех.
Наконец,
учтем то обстоятельство, что мощность квантования на выходе ФНЧ распределена
в полосе частот 0  fМАКС, где ,
fМАКС, где ,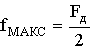 . Тогда РШ КВ на 1 Гц полосы частот в общем
виде имеет выражение:
. Тогда РШ КВ на 1 Гц полосы частот в общем
виде имеет выражение:
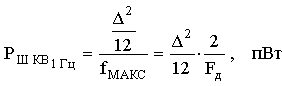
Формула 3.4
Для оценки
действия помех в каналах систем передачи пользуются параметром, который называется
защищенностью и
определяется следующим образом:
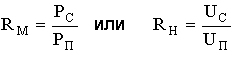
в относительных
единицах, АЗ = 10 lg RМ, дБм или АЗ = 20 lg RН, дБм в логарифмических единицах,
где РС, РП,
UС,
UП - мощности и напряжения сигнала и помехи соответственно.Величина
средней мощности телефонного сигнала при передаче по каналу ТЧ известна и
равна величине РСР ТФ = 32 мВт.Отсюда допустимая защищенность от шумов квантования

Средняя
мощность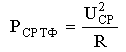 на единичном сопротивлении равна
на единичном сопротивлении равна  .Телефонный (ТФ) сигнал имеет характеристику, называемую пик-фактором:
.Телефонный (ТФ) сигнал имеет характеристику, называемую пик-фактором:

а UМАКС зависит от шага квантования и их числа (3.1): UМАКС = lМАКС  1/2, где множитель 1/2 учитывает квантование по уровню двухполярного сигнала. Тогда
1/2, где множитель 1/2 учитывает квантование по уровню двухполярного сигнала. Тогда
ТФ сигнал
в канале ТЧ передается в полосе частот 0,3 3,4
кГц, ширина полосы частот
3,4
кГц, ширина полосы частот  fТЧ = 3,4 - 0,3 = 3,1 кГц, и мощность ТФ сигнала
на 1 Гц полосы частот равна:
fТЧ = 3,4 - 0,3 = 3,1 кГц, и мощность ТФ сигнала
на 1 Гц полосы частот равна:

Формула 3.5
Поставим (3.4) и (3.5) в выражение для защищенности RШ КВ м, приравняем его допустимому значению RШ КВ доп

Формула 3.6
и определим lМАКС при передаче ТФ сигнала в канале ЦСП с ИКМ, учитывая что q = (50 70), Fд = 8 кГц;
70), Fд = 8 кГц;
 fТЧ = 3,1 кГц,
fТЧ = 3,1 кГц,
а RШ
КВ доп =
1,8*10^3: lМАКС = 1080 1510
Такое число уровней квантования оказывается чрезмерно большим, но его можно значительно снизить, принудительно уменьшая пик-фактор ТФ сигнала на передаче и восстанавливая его на приеме. Так, если уменьшить пик-фактор на передаче до величины q = 4,75 количество уровней квантования также резко уменьшится и составит величину lМАКС = 102.На практике изменение и восстановление пик-фактора сигнала (или динамического диапазона) осуществляется при помощи системы компандирования: на передающей стороне на входе АЦП включается устройство, которое называется компрессором (сжимателем) динамического диапазона, а на приеме на выходе ЦАП включается экспандер (расширитель) динамического диапазона. То есть в обощенную структурную схему рисунок 1.3 вводятся дополнительные блоки, как показано на рисунке 3.5.
Рисунок
3.5 - Система компандирования
в ЦСП с ИКМ.
Для того, чтобы избежать искажений при передаче сигналов компрессор (К) и экспандер (Э) должны иметь взаимнообратные амплитудные характеристики, как показано на рисунке 3.6.Здесь кривая 1 - амплитудная характеристика компрессора, кривая 2 - амплитудная характеристика экспандера, кривая 3 - результирующая амплитудная характеристика цепи компрессор-экспандер, которая должна быть линейной.Как видно из рисунка 3.6, значительно увеличивается амплитуда малых сигналов (отсчет 1) и мало меняется амплитуде больших сигналов (отсчет 2), то есть уменьшается как динамический диапазон сигнала 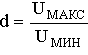 так и пик-фактор
так и пик-фактор 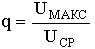 .
.
Рисунок
3.6 - Использование компандерных устройств для сжатия динамического диапазона:
а - амплитудные характеристики компандера;
б - сигнал на выходе компрессора.
Итак, отметим что операция квантования по уровню позволяет преобразовать бесконечное множество отсчетных значений аналогового сигнала в конечное множество разрешенных уровней, перенумеровать эти уровни и передавать информацию об амплитуде отсчета в виде двоичной кодовой комбинации с ИКМ. Для уменьшения числа разрешенных уровней квантования применяется нелинейная операция сжатия динамического диапазона сигнала.
Выводы по разделу
Операция квантования по уровню позволяет преобразовать бесконечное множество отсчётных значений аналогового сигнала в конечное множество разрешённых уровней, перенумеровать эти уровни и передавать информацию об амплитуде отсчёта в виде двоичной кодовой комбинации с ИКМ. Для уменьшения числа разрешённых уровней квантования применяется нелинейная операция сжатия динамического диапазона сигнала.
3.3 Кодирование
Операция
кодирования заключается в преобразовании номера "разрешенного" уровня в кодовую комбинацию двоичной системы счисления, состоящую из m символов вида "0" и "1",
где величина m называется разрядностью кода. Существует большое число двоичных
систем кодирования, однако в ЦСП с ИКМ нашли применение натуральный двоичный
код и его модификация - симметричный двоичный код.При использовании натурального кода любое положительное десятичное число li, не превышающее величины lМАКС (li = 0, lМАКС), может быть представлено в виде комбинации из m двоичных символов по следующему алгоритму:

m
- разрядность кода. Очевидно, что lМАКС определяется суммой весовых
составляющих вида 2 m - j при значении всех коэффициентов аj =
1:
lМАКС = 2 m - 1,
а суммарное
число "разрешенных" уровней
квантования I = lМАКС + 1 = 2 m (учитывая,
что кодируется и ноль).Поскольку в при передаче телефонных сигналов в каналах ЦСП с ИКМ используется двухполярное кодирование (для устранения постоянной составляющей и гармонических частот вида kFд k=(0,
= lМАКС + 1 = 2 m (учитывая,
что кодируется и ноль).Поскольку в при передаче телефонных сигналов в каналах ЦСП с ИКМ используется двухполярное кодирование (для устранения постоянной составляющей и гармонических частот вида kFд k=(0,  ) в указанных ЦСП используется симметричный двоичный код, в котором 1 или 0 в старшем разряде определяют полярность кодируемого сигнала с АИМ.Проиллюстрируем процесс кодирования при помощи простейшего примера.Пусть разрядность натурального двоичного кода m = 4. Тогда образующий полином примет вид:
) в указанных ЦСП используется симметричный двоичный код, в котором 1 или 0 в старшем разряде определяют полярность кодируемого сигнала с АИМ.Проиллюстрируем процесс кодирования при помощи простейшего примера.Пусть разрядность натурального двоичного кода m = 4. Тогда образующий полином примет вид:

при
этом lМАКС = 24 - 1 = 15, l? = 16, т.е. при помощи 4-х разрядной кодовой
комбинации можно закодировать не более 16 "разрешенных" уровней с номерами от 0 до 15. Предположим, что номер "разрешенного" уровня
li = 11, тогда двоичная комбинация в натуральном коде будет иметь вид:

При помощи симметричного двоичного кода первым символом кодовой комбинации кодируется знак отсчета:
li = +11=> 11011
li = -11=> 01011
В современных ЦСП с ИКМ операции квантования по уровню и кодирование на передаче реализуются в одном устройстве, называемом кодером: на его вход подается сигнал с АИМ-2, на выходе формируется цифровой двоичный сигнал с ИКМ. На приеме осуществляется обратное преобразование при помощи декодера.В общем случае двоичные коды по времени их появления разделяются на параллельные, если сигналы кодовой группы появляются одновременно, и последовательные, если сигналы кодовой группы появляются последовательно во времени, разряд за разрядом.
Выводы по разделу
Операция
кодирования заключается в преобразовании номера "разрешённого" уровня в кодовую комбинацию двоичной системы счисления, состоящую из m символов вида "0" и "1",
где величина m называется разрядностью кода. В ЦСП с ИКМ нашли применение
натуральный двоичный код и его модификация - симметричный двоичный код.Двоичные коды по времени их появления разделяются на параллельные, если сигналы кодовой группы появляются одновременно, и последовательные, если сигналы кодовой группы появляются последовательно во времени, разряд за разрядом.
3.4 Амплитудные характеристики канала ЦСП с ИКМ
Амплитудные характеристики каналов, показывающие зависимость изменения UВЫХот UВХ,или

в нормированных единицах, а ЦСП с ИКМ бывают двух типов:
- с равномерной
(линейной) шкалой квантования;
- с
неравномерной (нелинейной) шкалой квантования.
При линейном
квантовании как показано на рисунке 3.7 шаг квантования в зоне квантования
одинаков во всем рабочем динамическом диапазоне изменения входного сигнала
от UВХ МИН до UВХ МАКС, а амплитуда шума квантования
не превышает половины шага квантования:

При превышении UВХ некоторого
UВХ МАКС, наступает режим
ограничения:
 ,
где lМАКС =
2 m - 1, определяется разрядностью кода
m и при
использовании кодов конечной разрядности, любой входной сигнал UВХ
> UВХ МАКС будет передаваться в канале в виде сигнала UВЫХ = UВЫХ МАКС;
при
этом
возникают шумы ограничения, величина которых значительно превышает
шумы квантования: РШ ОГР > РШ КВ.
,
где lМАКС =
2 m - 1, определяется разрядностью кода
m и при
использовании кодов конечной разрядности, любой входной сигнал UВХ
> UВХ МАКС будет передаваться в канале в виде сигнала UВЫХ = UВЫХ МАКС;
при
этом
возникают шумы ограничения, величина которых значительно превышает
шумы квантования: РШ ОГР > РШ КВ.

Рисунок
3.7 - Линейное квантование
по уровню:
а) амплитудная характеристика; б) шумы квантования.
Мощность шума квантования при равномерной шкале квантования является величиной постоянной:
PШ КВ= 2/12 . При
динамическом диапазоне телефонного сигнала равном 40 дБ:
2/12 . При
динамическом диапазоне телефонного сигнала равном 40 дБ:

где PМАКСтф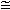 0
Дб PМИНтф= -40 Дб норма на величину защищенности
от шумов квантования, равная АЗ Ш КВ доп =
10 lg
RШ КВ доп= 33
0
Дб PМИНтф= -40 Дб норма на величину защищенности
от шумов квантования, равная АЗ Ш КВ доп =
10 lg
RШ КВ доп= 33  35 дБ (см. формулу 3.6), должна выполняться для всего динамического
диапазона ТФ сигнала.То есть
АЗ Ш КВ доп оказывается большей, чем величина АЗ Ш КВ МИН = РМИН ТФ - РШ
КВ = 35 дБ во всем динамическом
диапазоне ТФ сигнала, как показано на рисунке 3.8.Разрядность
кодовой комбинации,
при которой выполняется норма наАЗ Ш КВ доп можно определить из выражения (3.6):
35 дБ (см. формулу 3.6), должна выполняться для всего динамического
диапазона ТФ сигнала.То есть
АЗ Ш КВ доп оказывается большей, чем величина АЗ Ш КВ МИН = РМИН ТФ - РШ
КВ = 35 дБ во всем динамическом
диапазоне ТФ сигнала, как показано на рисунке 3.8.Разрядность
кодовой комбинации,
при которой выполняется норма наАЗ Ш КВ доп можно определить из выражения (3.6):

Рисунок
3.8 - Защищенность от шумов
квантования при линейном квантовании.
Пик-фактор Q речевого сигнала равен величине Q = 14  17 дБ, однако в каналах ЦСП с ИКМ передаются ТФ сигналы абонентской телефонной сети, причем для наиболее удаленных абонентов Q = 30
17 дБ, однако в каналах ЦСП с ИКМ передаются ТФ сигналы абонентской телефонной сети, причем для наиболее удаленных абонентов Q = 30  35
дБ, как показано на рисунке 3.8.Если требуется обеспечить защищенность от шумов квантования во всем динамическом диапазоне сигнала не менее, чем АЗ Ш КВ доп = 35 дБ, то потребуется m = 11 (из формулы 3.7), а с учетом двухполярного кодирования m = 12. При этом защищенность для сигналов с максимальной амплитудой (PМАКСтф) будет на 40 дБ превышать допустимое значение защищенности АЗ Ш КВ доп = 35 дБ.Большое число разрядов в коде (m = 12) при равномерном квантовании приводит к усложнению аппаратуры ЦСП с ИКМ и неоправданному увеличению частоты передачи кодовых импульсных комбинаций (тактовой частоты в канале).Устранить указанный существенный недостаток можно, осуществляя неравномерное (нелинейное) квантование, которое используется в современных ЦСП.Сущность неравномерного квантования заключается в следующем. Для малых по амплитуде ТФ сигналов шаг квантования выбирается минимальным и постепенно увеличивается, достигая максимальных значений для больших по амплитуде ТФ сигналов, как показано на рисунке 3.9.При
этом РШ КВ возрастает с увеличение шага квантования для больших по мощности ТФ
сигналов, однако их отношение
35
дБ, как показано на рисунке 3.8.Если требуется обеспечить защищенность от шумов квантования во всем динамическом диапазоне сигнала не менее, чем АЗ Ш КВ доп = 35 дБ, то потребуется m = 11 (из формулы 3.7), а с учетом двухполярного кодирования m = 12. При этом защищенность для сигналов с максимальной амплитудой (PМАКСтф) будет на 40 дБ превышать допустимое значение защищенности АЗ Ш КВ доп = 35 дБ.Большое число разрядов в коде (m = 12) при равномерном квантовании приводит к усложнению аппаратуры ЦСП с ИКМ и неоправданному увеличению частоты передачи кодовых импульсных комбинаций (тактовой частоты в канале).Устранить указанный существенный недостаток можно, осуществляя неравномерное (нелинейное) квантование, которое используется в современных ЦСП.Сущность неравномерного квантования заключается в следующем. Для малых по амплитуде ТФ сигналов шаг квантования выбирается минимальным и постепенно увеличивается, достигая максимальных значений для больших по амплитуде ТФ сигналов, как показано на рисунке 3.9.При
этом РШ КВ возрастает с увеличение шага квантования для больших по мощности ТФ
сигналов, однако их отношение
 стремится
к постоянной величине. Таким образом происходит выравнивание АЗ Ш КВ во
всем динамическом диапазоне изменения уровней ТФ сигнала:
стремится
к постоянной величине. Таким образом происходит выравнивание АЗ Ш КВ во
всем динамическом диапазоне изменения уровней ТФ сигнала:

АЗ Ш КВ = 10 lg RШ КВ 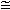 АЗ Ш КВ доп
АЗ Ш КВ доп 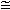 35 дБ, как показано на рисунке 3.10.
35 дБ, как показано на рисунке 3.10.
Рисунок
3.9 - Нелинейное квантование по уровню:
а) амплитудная характеристика; б) шумы квантования.
При нелинейном квантовании общее число уровней квантования уменьшается по сравнению с линейным в том же динамическом диапазоне сигнала (рисунки 3.7 и 3.9). В результате удается снизить разрядность кодовой канальной комбинации до m = 8 (l = 2 8 = 256). Во всех современных ЦСП с ИКМ (как PDH, так и SDH) канальные кодовые комбинации при передачи речи формируются при помощи нелинейного восьмиразрядного кодирования.
= 2 8 = 256). Во всех современных ЦСП с ИКМ (как PDH, так и SDH) канальные кодовые комбинации при передачи речи формируются при помощи нелинейного восьмиразрядного кодирования.
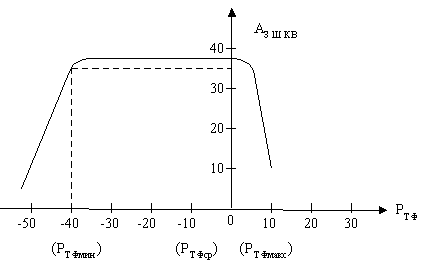
Рисунок
3.10 - Защищенность от шумов квантования при нелинейном кодировании.
Эффект неравномерного квантования может быть получен путем сжатия динамического диапазона сигнала с последующим равномерным квантованием и обратным преобразованием на приеме при помощи системы компандирования, по алгоритму приведенному в разделе 3.2 (рисунок 3.5). Этот способ применялся в ЦСП с ИКМ первых выпусков (60  70-ые годы XX века).В настоящее время нелинейное кодирование осуществляется путем реализации логарифмической амплитудной характеристики, когда передается не эффективное напряжение ТФ сигнала, а его логарифмическое значение, что эквивалентно сжатию динамического диапазона. Используются две логарифмические характеристики типа А и (, которые удобно изображать и описывать в нормированном виде у = f (х), где
70-ые годы XX века).В настоящее время нелинейное кодирование осуществляется путем реализации логарифмической амплитудной характеристики, когда передается не эффективное напряжение ТФ сигнала, а его логарифмическое значение, что эквивалентно сжатию динамического диапазона. Используются две логарифмические характеристики типа А и (, которые удобно изображать и описывать в нормированном виде у = f (х), где
где А = 87,6 и  = 255.
= 255.
Процесс логарифмирования (сжатия (компрессии) динамического диапазона) и кодирования, а также обратная операция декодирования и расширения (экпандирования), реализуется в цифровом виде в нелинейных кодерах и декодерах (кодеки), алгоритмы работы которых и схемная реализация в данном разделе не рассматриваются.Характеристика компандирования типа А используется в ЦСП с ИКМ соответствующих европейской иерархии, а типа  - в ЦСП с ИКМ, соответствующих совероамериканской иерархии.
- в ЦСП с ИКМ, соответствующих совероамериканской иерархии.
Выводы по разделу
Амплитудные характеристики каналов бывают двух типов:
- С равномерной
(линейной) шкалой квантования;
- С
неравномерной (нелинейной) шкалой квантования.
При линейном квантовании шаг квантования в зоне квантования одинаков во всём рабочем динамическом диапазоне, а амплитуда шума квантования не превышает половины шага квантования.
Мощность шума квантования является величиной постоянной.
Большое число разрядов в коде (m =12) при равномерном квантовании приводит к усложнению аппаратуры ЦСП с ИКМ и неоправданному увеличению частоты передачи кодовых импульсных комбинаций.
Устранить этот недостаток можно, осуществляя неравномерное квантование, которое используется в современных ЦСП.
Сущность неравномерного квантования:
Для малых по амплитуде ТФ сигналов шаг квантования выбирается минимальным и постепенно увеличивается, достигая максимальных значений для больших по амплитуде ТФ сигналов.
При нелинейном квантовании общее число уровней квантования уменьшается по сравнению с линейным в том же динамическом диапазоне сигнала, в результате удаётся снизить разрядность кодовой канальной комбинации до m = 8.
Контрольные вопросы
- В
чём суть кодирования квантованного по уровню сигнала?
- Какие
существуют типы кодов?
- 3.Суть
операции квантования?
- Что
такое уровень и шаг квантования?
- Что
такое ошибка квантования, ошибка ограничения?
- Что
такое защищённость и для чего ею пользуются?
- Сущность
теоремы Котельникова?
- Что
такое АИМ-1 и АИМ-2, как они получаются?
- Какой
спектр имеют сигналы АИМ-1 и АИМ-2?
- Нарисовать
различные типы амплитудных характеристик, указать достоинства и недостатки?
- Что
такое неравномерная шкала квантования, необходимость её применения и способы
её получения?
- Норма
на величину защищённости от шумов квантования?
Примеры решения задач
Пример 1
Определить
относительную полосу расфильтровки, если известен спектр исходного сигнала
0,3 -- 4,00 кГц и частота дискретизации FД = 10 кГц.
Решение:

1. Определяем абсолютную полосу расфильтровки:
 FР =
(FД
- FМАКС) - FМАКС = FД
- 2 FМАКС
FР =
(FД
- FМАКС) - FМАКС = FД
- 2 FМАКС
 FР = 10
- 2 * 4 = 2 кГц.
FР = 10
- 2 * 4 = 2 кГц.
2. Определяем относительную полосу расфильтровки:
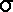 =
=
 FР/ f0 =
FР/ f0 =  FР
/ (FД / 2) =
2 / (10 / 2) = 0,4.
FР
/ (FД / 2) =
2 / (10 / 2) = 0,4.
Ответ: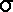 = 0,4
= 0,4
Пример 2
Закодировать отсчет напряжения сигнала с помощью простого прямого кода, если UАИМ = 45,3 mB;  = 1,0 mB; m = 7. Какова ошибка квантования(
= 1,0 mB; m = 7. Какова ошибка квантования(
Решение:
- Определяем
квантованное значение сигнала UКВ= 45 mB.
-
Определяем номер уровня квантования:
N = UКВ/ ,
подставляем значения и получим N = 45/1 = 45.
,
подставляем значения и получим N = 45/1 = 45.
-
Определяем коэффициенты двоичного кода:
N = 0
* 26 + 1 * 25 + 0 * 24 + 1 * 23 + 1 * 22 + 0 * 21 + 1 * 20 следовательно
получим ответ: 0101101.
-
Определяем ошибку квантования
 =
UАИМ- UКВ = 45,3
=
UАИМ- UКВ = 45,3  45
= 0,3 mB.
45
= 0,3 mB.
Ответ:  =0.3 mB, 0101101.
=0.3 mB, 0101101.
Пример 3
Определить число уровней квантования для минимально допустимого значения АКВ=25 дБ, если Q=35 дБ.
Решение:
-
Определяем разрядность кода m = (АКВ + Q - 5.58) / 6
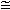 10.
10.
-
Определяем число уровней NКВ = 210 = 1024.
Ответ: N = 1024.
Пример 4
Закодировать отчеты напряжения аналогового сигнала с помощью симметричного кода, если UАИМ1 = -24,4 mB, UАИМ2 = 36,2 mB,  = 0,5 mB,
= 0,5 mB,
m = 8.
Решение:
- 1. Определяем квантованное значение сигнала:
UКВ1 = (24,5 mB, UКВ2 = 36 mB.
- 2. Определяем номер уровня квантования: N1 = (49, N2 = 72.
- 3. Определяем коэффициенты двоичного кода.
Так как у нас код симметричный, то первый знак будет указывать положительный или отрицательный уровень квантования.
"0" ( отрицательный, а "1" (
положительный уровень.
N1 =
0*26 + 1*25 + 1*24 + 0*23 + 0*22 +0*21 + 1*20, получаем 0.0110001
N2 =
1*26 + 0*25 + 0*24 + 1*23 + 0*22 +0*21 + 0*20, получаем 1.1001000
Ответ: 0.0110001; 1.1001000.
Задачи для тестирования
Задача 1
Определить необходимую разрядность кода для кодирования второго отсчёта с использованием АДИКМ и ИКМ.

Ответ: При использовании ИКМ необходимая разрядность 28, а при использовании АДИКМ разрядность будет составлять 24 .
Задача 2
Определите напряжение шума квантования (перегрузки), при ДМ, если ?=0,05.

Ответ: Uпер=0,5.
 , изменяется в соответствии с изменением
модулирующего сигнала с(t) на интервале времени передачи отсчета (и, а
при АИМ-2 амплитуда каждого отсчета постоянна и равна значению модулирующего
сигнала в начальный момент отсчета. На рисунке 3.1 представлен исходный
модулирующий
сигнал с(t), а также сигналы АИМ-1 и АИМ-2 в случае дискретизации двухуровневых
сигналов.Сигналы АИМ-1 и АИМ-2 в общем случае имеют различную форму, а значит их частотные спектры G1(f) и G2(f), определяемые преобразованием Фурье:
, изменяется в соответствии с изменением
модулирующего сигнала с(t) на интервале времени передачи отсчета (и, а
при АИМ-2 амплитуда каждого отсчета постоянна и равна значению модулирующего
сигнала в начальный момент отсчета. На рисунке 3.1 представлен исходный
модулирующий
сигнал с(t), а также сигналы АИМ-1 и АИМ-2 в случае дискретизации двухуровневых
сигналов.Сигналы АИМ-1 и АИМ-2 в общем случае имеют различную форму, а значит их частотные спектры G1(f) и G2(f), определяемые преобразованием Фурье:

 и=Tи/N,
N - число каналов.Легко показать, что при
T
и=Tи/N,
N - число каналов.Легко показать, что при
T 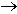
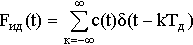


 FМАКС;
FМАКС; (FМИН
(FМИН
 .
Если амплитуда отсчета сигнала UАИМ(t)
в пределах двух соседних разрешенных значений превышает половину шага квантования
.
Если амплитуда отсчета сигнала UАИМ(t)
в пределах двух соседних разрешенных значений превышает половину шага квантования
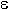 Ш КВ(t) =
UАИМ(t) - UКВ(t),
при этом |
Ш КВ(t) =
UАИМ(t) - UКВ(t),
при этом | Ш КВ (t)|
Ш КВ (t)|  < f <
< f <



 на выходе канала тональной
частоты (ТЧ) эталонной цепи в точке нулевого относительного уровня (ТНОУ)
в час наибольшей нагрузки (ЧНН) не должна превышать величины Р
на выходе канала тональной
частоты (ТЧ) эталонной цепи в точке нулевого относительного уровня (ТНОУ)
в час наибольшей нагрузки (ЧНН) не должна превышать величины Р

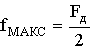 . Тогда РШ КВ на 1 Гц полосы частот в общем
виде имеет выражение:
. Тогда РШ КВ на 1 Гц полосы частот в общем
виде имеет выражение: 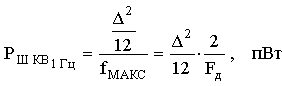
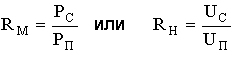

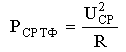 на единичном сопротивлении равна
на единичном сопротивлении равна 




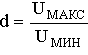 так и пик-фактор
так и пик-фактор 
 = lМАКС + 1 = 2 m (учитывая,
что кодируется и ноль).Поскольку в при передаче телефонных сигналов в каналах ЦСП с ИКМ используется двухполярное кодирование (для устранения постоянной составляющей и гармонических частот вида kFд k=(0,
= lМАКС + 1 = 2 m (учитывая,
что кодируется и ноль).Поскольку в при передаче телефонных сигналов в каналах ЦСП с ИКМ используется двухполярное кодирование (для устранения постоянной составляющей и гармонических частот вида kFд k=(0, 



 ,
где lМАКС =
2 m - 1, определяется разрядностью кода
m и при
использовании кодов конечной разрядности, любой входной сигнал UВХ
> UВХ МАКС будет передаваться в канале в виде сигнала UВЫХ = UВЫХ МАКС;
при
этом
возникают шумы ограничения, величина которых значительно превышает
шумы квантования: РШ ОГР > РШ КВ.
,
где lМАКС =
2 m - 1, определяется разрядностью кода
m и при
использовании кодов конечной разрядности, любой входной сигнал UВХ
> UВХ МАКС будет передаваться в канале в виде сигнала UВЫХ = UВЫХ МАКС;
при
этом
возникают шумы ограничения, величина которых значительно превышает
шумы квантования: РШ ОГР > РШ КВ. 

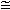 0
Дб PМИНтф= -40 Дб норма на величину защищенности
от шумов квантования, равная АЗ Ш КВ доп =
10 lg
RШ КВ доп= 33
0
Дб PМИНтф= -40 Дб норма на величину защищенности
от шумов квантования, равная АЗ Ш КВ доп =
10 lg
RШ КВ доп= 33 


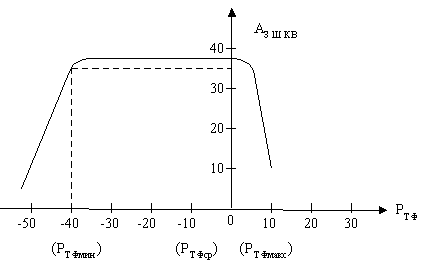

 = 255.
= 255. 
 =
=

