Лекция №13

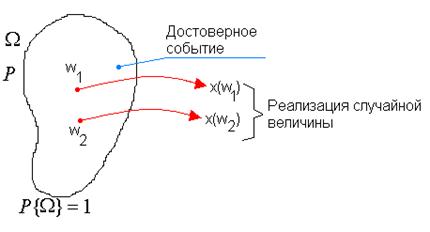
Случайные процессы

Случайные величины

-   Случайная величина

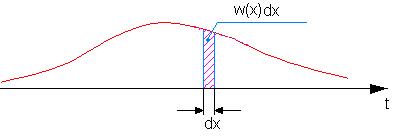
Реализация есть конкретное значение случайной величины

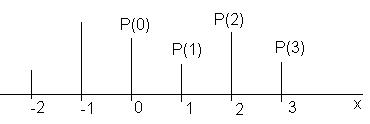
Суммарная длинна отрезков  = 1

- условие нормировки

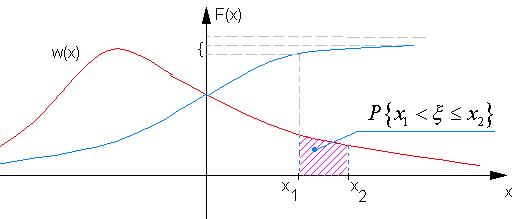
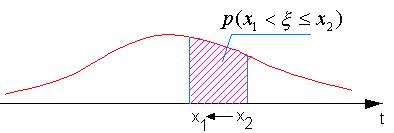
Функция распределения

- функция является неубывающей и неотрицательной

Плотность распределения вероятности

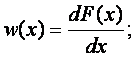
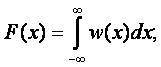
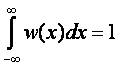
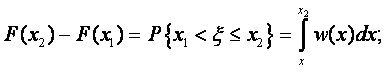
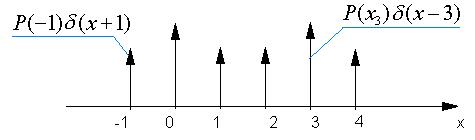
Для дискретной случайной величины функция распределения будет выглядеть следующим образом:

Характеристическая функция

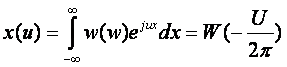
 - где W – преобразование Фурье от w(*)

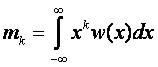
-   начальный момент k-того порядка

Первый момент:

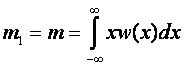
- математическое ожидание случайной величины            (среднее)

Медиана делит площадь попалим. Если кривая будет симметричной, то эти 3 характеристики совпадут

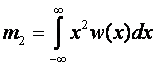Второй момент:

 - среды квадратов случайных величин

 - центральный момент k-го порядка.

      k-ый центральный момент  = k-му начальному моменту центрированной случайной величины, полученной вычитанием  из случайной величины его среднего (мат. ожидания)

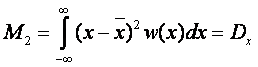
 - дисперсия случайной величины

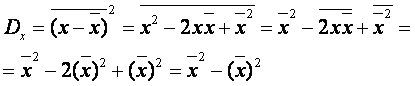
Асимметрия плотности распределения и эксцесс

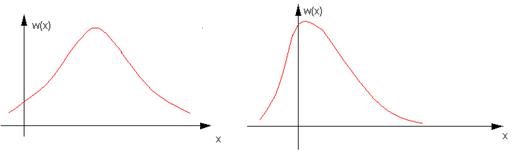
Рассмотрим  Х1    и    Х2 

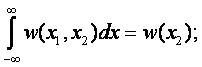
- Маргинальная плотность распределение вероятности

- смешанный начальный момент порядка (k, m)

-   ковариационный момент

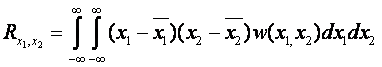
- корреляционный момент

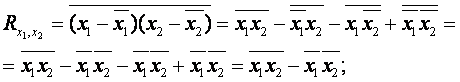
- совместная (n-мерная) плотность распределения вероятности

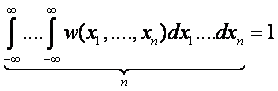
       Исчерпывающее описание случайного процесса – это его совместная  n-мерная плотность распределения вероятности для любых n

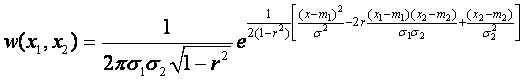
 - Гауссово пространство (одномерная)

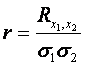
- Нормированный коэффициент корреляции