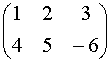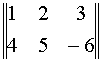
Линейная алгебра 

1.1. Определители и матрицы 

назад | оглавление | вперёд

Понятие числовой матрицы

Числовая матрица – прямоугольная таблица чисел, состоящая из строк и столбцов. Размеры матрицы обозначаются M * N, где M-число строк, N-число столбцов.

Пример:

A= 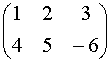Числовая матрица или A=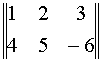Числовая матрица

Общее обозначение:

A=Числовая матрица или A=Числовая матрица

, где элемент матрицы- элемент матрицы, находящийся на пересечении i-ой строки и j-ого столбца: i-ой строки j-ого столбца

Если M=N, то матрица называется квадратной. В этом случае

N – ее порядок . В квадратной матрице выделяются две диогонали –главная и побочная:

. .           . .

. . главная . . . побочная

. .           . .

Пример:

A = 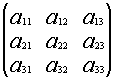Пример главную диогональ образуют эл-ты:

главную диогональ образуют эл-ты , а побочную побочную

Определители второго порядка.

Пусть дана матрица второго порядка A= дана матрица второго порядка.

Определителем второго порядка называется число, вычисляемое по правилу:

вычисляемое по правилу

Определитель второго порядка равен произведению элементов

Главной диогонали минус произведение элементов Побочной дио-

гонали.

Главной диогонали минус произведение элементов Побочной дио-= 1*(-4)-6 = -10

Подматрица, минор, алгебраическое дополнение.

Пусть дана какая-либо матрица (например, порядка 3):

А= дана какая-либо матрица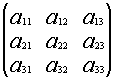

Подматрицей матрицы А называется часть этой матрицы, полученная вычеркиванием какого-либо количества строк, и(или) какого-либо количества столбцов.

Например, если вычеркнуть первую строку и второй столбец ,то получим подматрицу даной матрицы:

получим подматрицу даной матрицы

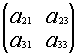
Минором Минором элемента элемента определителя определителя называется определитель, полученный вычеркиванием i-ой строки и j-ого столбца.

Алгебраическим дополнением элемента Алгебраическим дополнением называется минор, взятый со знаком “+” или “- ” в зависимости от места этого элемента в определителе.

Обозначение: Обозначение=ОбозначениеОбозначение

Если i+j - четное число , то знак алгебраического дополнения

и минора одинаковы, если нечетное , то их знаки противоположны.

Символически покажем положительные и отрицательные места в определителе:

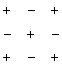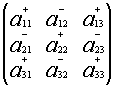
положительные и отрицательные места в определителе или положительные и отрицательные места в определителе

ОПРЕДЕЛИТЕЛИ ТРЕТЬЕГО ПОРЯДКА.

Определителем третьего порядка называется число, вычисляемое по правилу:

= Определителем третьего порядка называется число, вычисляемое по правилу =

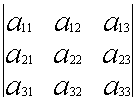Определитель третьего порядка равен сумме произведений элементов первой строки на их алгебраические дополнения.

Заменим алгебраические дополнения на миноры:

алгебраические дополнения на миноры = алгебраические дополнения на миноры

= алгебраические дополнения на миноры - алгебраические дополнения на миноры + алгебраические дополнения на миноры

Вычисляя миноры, получим:

= Вычисляя миноры, получим

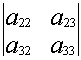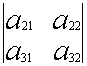
Вычисляя миноры, получим

СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ.

Свойство 1.

При замене строк на столбцы определитель не меняется.

При замене строк на столбцы определитель не меняется = При замене строк на столбцы определитель не меняется

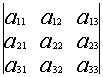(такая операция называется транспонированием).

Следствие: строки и столбцы равноправны ,т.е любые свойства или утверждения относительно строк справедливы и для столбцов и наоборот.

Свойство 2.

При перестановке двух строк определитель меняет знак

на противоположный.

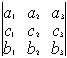
При перестановке двух строк определитель меняет знак = - При перестановке двух строк определитель меняет знак

Следствие: любую строку (столбец ) можно поставить первой (первым)

Свойство 3.

Определитель с двумя равными строками равен нулю.

Определитель с двумя равными строками равен нулю = 0

Свойство 4.

Общий множитель элементов строки можно выносить за знак определителя.

Общий множитель элементов строки можно выносить за знак определителя Общий множитель элементов строки можно выносить за знак определителя Общий множитель элементов строки можно выносить за знак определителя

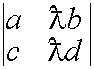
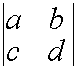
Следствие :

Постоянный множитель можно внести в какую-нибудь строку

Постоянный множитель можно внести в какую-нибудь строку Постоянный множитель можно внести в какую-нибудь строку

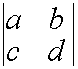
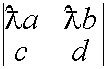
Свойство 5.

Если элементы какой –либо строки состоят из двух слагаемых,

то определитель можно представить в виде суммы двух определите-

лей.

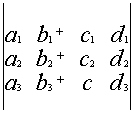
в виде суммы двух определите- в виде суммы двух определите- в виде суммы двух определите-

Свойство 6.

Определитель не меняется ,если любую строку умножить на любое

число и прибавить к любой другой строке.

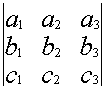
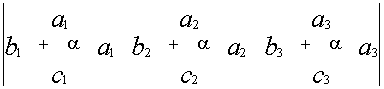
Определитель не меняетсяОпределитель не меняется

Случаи ,когда определитель равен нулю:

  1. Все элементы какой-либо строки равны нулю
  2. Две строки одинаковы
  3. Элементы двух строк пропорциональны

ОПРЕДЕЛИТЕЛИ ПОРЯДКА n.

Вычисление определителей порядка n.

Для вычисления порядка n используется метод разложения по cтроке.

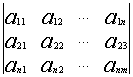
Для вычисления порядка nДля вычисления порядка n Для вычисления порядка n

Алгебраическое дополнение получается вычеркиванием i-строки

и j-столбца. Этот процесс мы будем продолжать до тех пор пока

не получим определители порядка 2 или 3

получим определители порядка 2 или 3 получим определители порядка 2 или 3 получим определители порядка 2 или 3

Формулу (1) используют как правило при i=1

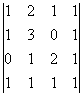
Пример:

используют как правило при i=1 используют как правило при i=1 используют как правило при i=1

 

назад | оглавление | вперёд