Понятие системы линейных уравнений.

Система линейных уравнений порядка n имеет вид:

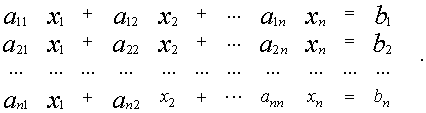
При этом числа -называются коэфициентами при неизвестных

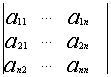Матрица называется матрицей системы

Числа 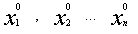- решение системы,если при подстановке этих чисел в систему каждое из уравнений системы превращается в верное числовое тождество.

Система линейных уравнений называется совместной, если она имеет по крайней мере одно решение.

Если система линейных уравнений не имеет решений , то система называется несовместной.

Формулы Крамера

Расмотрим систему уравнений (*). И пусть А- матрица системы

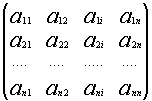
Если i –столбец заменим свободными членами , то соответствующую матрицу обозначим

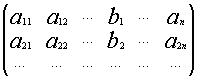
Если система линейных уравнений (*) такова, что определитель

системы отличен от нуля ,то система линейных уравнений имеет

единственое решение , которое находится по формуле:

назад | оглавление | вперёд