Линейная алгебра 

1.3. Матрицы. Операции над матрицами 

назад | оглавление | вперёд

Две матрицы A и B называются равными ,если они имеют

один и тот же порядок и если элементы стоящие на соответствующих местах равны.

Две матрицы A и B называются равными Две матрицы A и B называются равнымиДве матрицы A и B называются равными

К линейным операциям относятся :

Умножение матрицы на число

Для того чтобы умножить матрицу на число нужно каждый элемент

матрицы умножить на это число:

Умножение матрицы на числоУмножение матрицы на числоУмножение матрицы на число

Сложение матриц.

Складывать можно только матрицы одинаковых размеров:

Складывать можно только матрицы одинаковых размеров

Свойства линейных операций

Свойства линейных операций

Свойства линейных операций

Свойства линейных операций

Свойства линейных операций

Свойства линейных операций

Если матрица в качестве элементов имеет нули , то такая матрица называется нулевой.

Произведение матриц .

Произведение матриц Произведение матрицПроизведение матриц

Произведение матриц Произведение матрицПроизведение матриц

Произведение матриц

Произведение матрицПроизведение матриц

Произведение матриц

Пример:

Пример: Пример:

Пример:.Пример:=Пример:=Пример:

Пример:.Пример:=Пример:

Пример:.

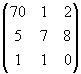
Если для матриц А и В выполняется равенство А* В=В*А ,то

матрицы называются перестановочными.

Если для матриц А , В , С имеет смысл операция произведения,

то выполняются равенства

A(B*C)=(A*B)*C

A(B+C)=AB+AC

(B+C)A=BA+CA

Транспонирование матриц

Рассмотрим матрицы

Транспонирование матриц Транспонирование матриц

AT называется транспонированной по отношению к A

Если AT получена из матрицы А заменой строк на столбцы то

Транспонирование матриц

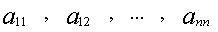назавают главной диагональю назавают главной диагональю

Очевидно:

Если А является квадратной матрицей(n*n), то элементы матрицы

Если для квадратной матрицы выполняется условие

Если для квадратной матрицы выполняется условие

то матрица А называется симметричной и в этом случае достаточно указать элементы, стоящие на главной диагонали и элементы, стоящие над главной диагональю.

Понятие обратной матрицы.

Обратные матрицы существуют только для квадратных матриц. Квадратная матрица ,у которой на главной диагонали стоят

единицы, а вне главной диагонали - нули, называется единичной матрицей.

Например, единичная матрица второго порядка:

единичная матрица второго порядкаединичная матрица второго порядка

Теорема.

Если А и В – квадратные матрицы одного и того же порядка n, то определитель их произведения равен произведению определителей матриц-сомножителей:

Если А и В – квадратные матрицы одного и того же порядка n

Определение обратной матрицы:

Матрица В называется обратной для матрицы А , если А и В перестановочны и А*В=В*А=Е

Обозначение обратной матрицы:

Обозначение обратной матрицы Обозначение обратной матрицы

Теорема.

Если матрица А имеет обратную ,то ее определитель отличен от

нуля.

Доказательство.

Так как А имеет обратную матрицу, то

Так как А имеет обратную матрицу, то Так как А имеет обратную матрицу, то

Воспользуемся теоремой о том ,что определитель произведения

равен произведению определителей.

равен произведению определителейравен произведению определителей

что и требовалось доказать.

Нахождение обратной матрицы методом Крамера

Теорема.

Если квадратная матрица А имеет определитель отличный от нуля, то данная матрица имеет обратную.

Доказательство.

Пусть матрица А такова, что её определитель отличен от нуля.

Докажем, что существует матрица В, такая что:

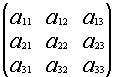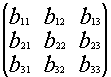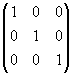
Нахождение обратной матрицы методом Крамера*Нахождение обратной матрицы методом Крамера=Нахождение обратной матрицы методом Крамера

 

Отсюда, в частности, следует:

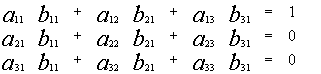
Нахождение обратной матрицы методом КрамераНахождение обратной матрицы методом Крамера

Система (3) –из трех уравнений с тремя неизвестными, и т.к. определитель системы (3) по условию отличен от нуля , то эту систему можно решить методом Крамера причем решение (3) - единственно.

Аналогично можно доказать существование и единственность всех остальных элементов матрицы В.

Алгоритм нахождения обратной матрицы методом Крамера.

Первоначально находим определитель матрицы А и если он

равен нулю , то обратной матрицы не существует.

Если определитель отличен от нуля , то находим союзную

определитель отличен от нуля матрицу

состоящую из алгебраических дополнений элементов матрицы А.

алгебраических дополнений элементов матрицы Аалгебраических дополнений элементов матрицы А

Элементарные преобразования матриц.

Эквивалентные матрицы.

К элементарным преобразованиям относятся:

  1. умножение любой строки матрицы на число , отличное от нуля;

    2. пример

    умножение любой строки матрицы на число , отличное от нуля= умножение любой строки матрицы на число , отличное от нуля
  2. к любой строке можно добавить любую другую строку , умноженую на любое число;
  3. перестановка двух строк.
    4.

Матрицы, полученные с помощью элементарных преобразований

называются эквивалентными

А~ В , В~ С , А~ С

Вычисление обратной матрицы с помощью элементарных преобразований.

Расмотрим квадратную матрицу А и предположим , что

Расмотрим квадратную матрицу А и предположим , что

тогда используя элементарные преобразования эту матрицу

можно привести к единичной матрице .Таким образом единичная

матрица эквивалентна любой невырожденой матрице того же

порядка.

Теорема

Если элементарные преобразования:

Если элементарные преобразования

переводят невырожденую матрицу А в единичную , то

те же самые преобразования, взятые в том же порядке, переводят

единичную матрицу в обратную для A.

Доказательство:

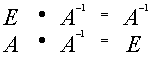
единичную матрицу в обратную для A единичную матрицу в обратную для A

единичную матрицу в обратную для A

отсюда

единичную матрицу в обратную для Aединичную матрицу в обратную для A

 

назад | оглавление | вперёд