Основные понятия.

Система уравнений вида:

называется линейной системой из n уравнений с m неизвестными.

(a_ij) коэффициенты при неизвестных x₁, x₂,...,x_m

b₁,b₂,...,b_n - свободные члены

Матрица А системы (*) состоит из коэффициентов a_ij, размера n*m .

Если неизвестные и свободные члены представим в виде: ,

то систему уравнений (*) мы можем переписать в виде: (3)

Запись системы в виде (3) называют матричной формой записи системы линейных уравнений (*) .Следует особо обратить внимание на то, что m может быть неравно n . Если m=n и матрица А является невырожденой , то из соотношения (3) вытекает: (4)

Равенство (4) получается умножением (3) слева на А-1. Система (*) называется совместной, если она имеет по крайней мере одно решение. В противном случае система называется несовместной. Решить систему - означает найти все её решения.

Метод Гаусса

Расмотрим систему (*):

Припишем к матрице А матрицу-столбец В

Припишем к матрице А матрицу-столбец В:

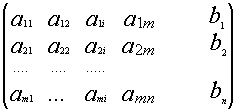
Матрица H называется расширенной матрицей системы. Матрица, у которой ниже главной диагонали стоят нули называется треугольной.Метод Гаусса (метод исключения неизвестных) состоит в том, что расширенную матрицу системы с помощью элементарных преобразований мы приводим к треугольному виду. Если у нас при этом получается матрица вида: то, система решений не имеет.

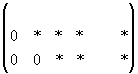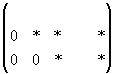Если треугольная матрица получается вида: ,то система имеет бесконечно много решений. При этом какие-то неизвестные обьявляются свободными, а остальные неизвестные могут быть выражены через них. Свободные неизвестные могут принимать любые значения. Если матрица примет вид: ,то этом случае система имеет единственное решение.

Пример:

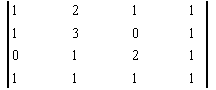
Элементарные преобразования расширенной матрицы системы, приводящие её к треугольному виду, могут быть такими:

~~

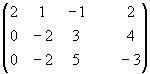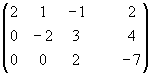
В итоге получим систему: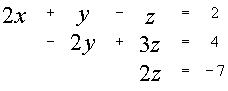

Откуда получим значения неизвестных: y = -7,25 x = 2,875

Пример: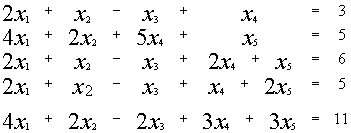

~~~

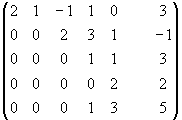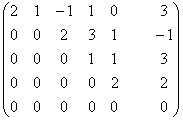
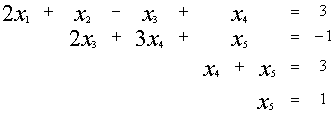
назад | оглавление | вперёд