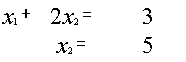1. Совместна или нет данная система
2. Если совместна, то сколько имеет решений а)единственное

б)беск.множество

Понятие ранга матрицы

А=() i= j=

Возьмем в матрице К строк и К столбцов, тогда элементы матрицы, стоящие на пересечении этих строк и столбцов образуют квадратную матрицу порядка К. Определитель этой квадратной матрицы называется минором порядка К для матрицы А.

Опр.1. Наибольший порядок минора матрицы,
отличный от нуля называется рангом матрицы.

Опр.2. Число r(A)=k называется рангом матрицы А, если среди миноров порядка k есть по крайней мере один,
отличный от нуля, а все миноры большего порядка равны нулю.

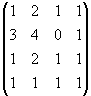М==0 М==-20 М==0 М=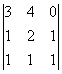=3 Ранг равен 3.

Совершенно очевидно, что нулевой ранг имеет только нулевая матрица. Если матрица не нулевая то её ранг1. С другой стороны если матрица имеет порядок MxN, то r(A)min(M,N).

Теоремы о ранге матриц

Т.1. Если матрица А эквивалентна матрице B, то ранг матрицы А равен рангу матрицы B (элементарные преобразования не изменяют ранга матрицы).

Доказательство. Для докозательства достаточно доказать, что каждое из преобразований не может изменить ранга матрицы.

1) А~B B получена умножением строки(столбца) на отличное от нуля число.

А= B=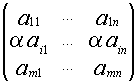

Если i-я строка не входит в выделенный минор то миноры матриц А и B совпадают. Если i-я строка входит в выделенный минор В=А(по св-ву определителей). Если минор А был отличен от нуля, то В будет отличен от нуля. Таким образом умножение на отличное от нуля число не изменяет ранг матрицы.

2) A~B B получена прибавлением строк

А= В=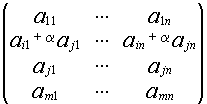

 

Если выбранные строки не содержат i-й строки, то соответствующие миноры матриц А и В полностью совпадают. Если минор матрицы А=0, то и минор матрицы В=0, если минор матрицы А0, то и минор матрицы В0.

Если выбранные миноры содержат i-ю и j-ю строки, тогда М(А)=А=

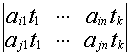
В=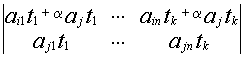

минор В получен из А путем прибавления строки.

3. Элементарные преобразования получаются с помощью конечного числа преобразований 1 и 2 типа и по уже доказанному на каждом из шагов ранг матрицы не меняется. Следовательно, он не изменится и за конечное число шагов. Ранг матрицы не меняется, если произведено конечное число элементарных преобразований.

Ответ: r(A)=2

А=() H=

Система ур-ний (*) совместна тогда и только тогда, когда ранг матрицы системы А равен рангу расширенной матрицы r(A)=r(H)

Если система совместна, то она имеет единственное решение, если r(A)=r(H)=n и его можно найти методами Крамера или Гаусса.

Если r(A)=r(H)=k<n, то система имеет бесконечно много решений. В этом случае n-k неизвестных обьявляются свободными неизвестными (принимают любые значения), оставшиеся k неизвестных выражаются через эти свободные неизвестные.

Если в системе (*) все свободные члены равны нулю, то такая система является однородной.

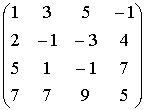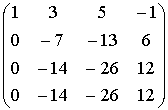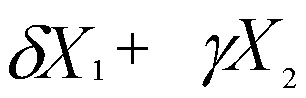
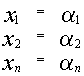Однородные системы всегда совместны т.к. ====0 всегда является решением. Такое решение называется тривиальным.

1) то

1) Если является решением системы, то 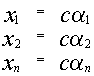также является решением.

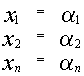2) Если является решением системы

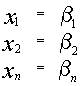также является решением той же самой системы, то и

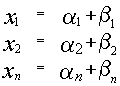также является решением системы

откуда получим

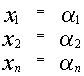3) Если и 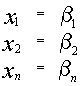два различных решения системы, то их линейная комбинация, равная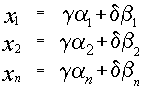

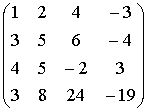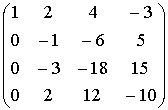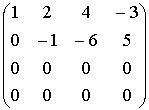
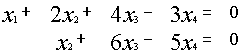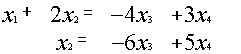
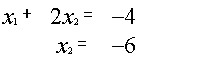Доказательство.

откуда получим

Каждое из решений системы можно записать в виде строки

матрицы, тогда на основании свойств можно утверждать, что матрицы есть решения, то также являются решением. Минимальная возможная система решений через которую выражаются все остальные решения называется фундаментальной системой решений.

назад | оглавление | вперёд