|
Аналитическая геометрия |
|
3.2 Уравнение прямой линии на плоскости |
назад | оглавление | вперёд |
Теорема: Всякое линейное
ур-ние вида ![]() (oбщее
ур-е прямой) определяет прямую на плоскости.
(oбщее
ур-е прямой) определяет прямую на плоскости.
Векторное ур-е прямой.
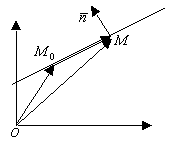
![]() ;
;![]() ;
;![]() ;
;![]()
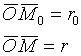 ;
;![]() -векторное
ур-е прямой
-векторное
ур-е прямой
![]() -ур-е
прямой проходящей через данную точку с данным нормальным вектором
-ур-е
прямой проходящей через данную точку с данным нормальным вектором ![]()
![]()
![]() -ур-е
прямой проходящей через данную точку с заданным вектором(каноническое ур-е)
-ур-е
прямой проходящей через данную точку с заданным вектором(каноническое ур-е)
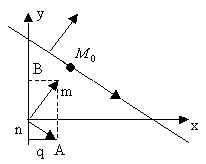
![]() ;
;![]() ,
т.к.
,
т.к.![]() или
или
![]()
![]() ,где
,где
![]() - ур-ние
прямой проходящей через заданную точку с данным угловым коэффициентом.
- ур-ние
прямой проходящей через заданную точку с данным угловым коэффициентом.
![]() -ур-ние
прямой с данным угловым коэффициентом.
-ур-ние
прямой с данным угловым коэффициентом.
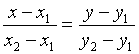 -ур-ние
прямой проходящей через 2 заданные точки.
-ур-ние
прямой проходящей через 2 заданные точки.
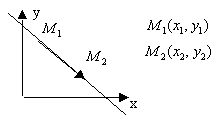
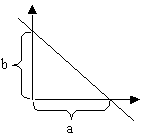
![]() - ур-ние прямой в отрезках
- ур-ние прямой в отрезках
![]() - нормальное
ур-е прямой
- нормальное
ур-е прямой
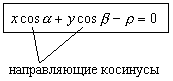
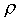 -расстояние
от начала координат до прямой
-расстояние
от начала координат до прямой 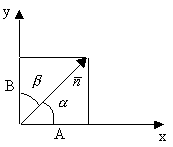
 ;
;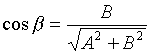
Параметрическое уравнение прямой.

Условие параллельности двух прямых.
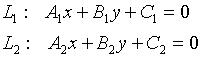

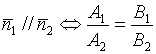 ;
;![]()
Условие перпендикулярности двух прямых.
![]()

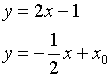
Угол между двумя прямыми
![]() .
.
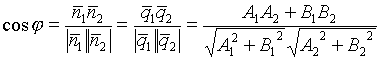 =
=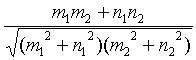

назад | оглавление | вперёд