Плоскость в пространстве.

Опр: Любое линейное уравнение от 3-х переменных определяет пл-ть в пространстве и обратно. - общее ур-е пл-ти в пространстве

-пл-ть проходит через начало координат

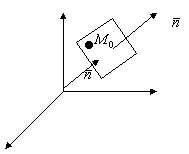
ур-е пл-ти, проходящей через данную точку и данный нормальный вектор

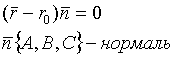
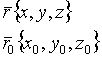
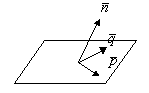
-направляющие вектора пл-ти

-смешанное произведение 3-х векторов

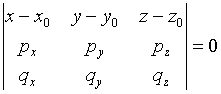- ур-е пл-ти проходящей через данную точку с данными направляющими векторами.

Пусть

x,y,z -текущие координаты

- ур-е пл-ти в отрезках.

Нормальное уравнение плоскости.

-нормальное ур-е пл-ти

p - расстояние от начала координат до плоскости.

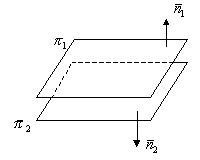
Условие параллельности двух плоскостей.

;

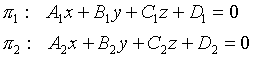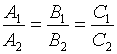
Условие перпендикулярности двух плоскостей.

;;

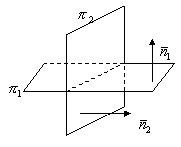Угол между плоскостями.

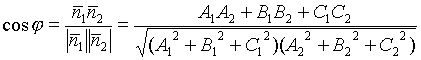
Прямая в пространстве.

- векторное ур-е прямой в пространстве

t= каноническое ур-е прямой

- параметрическое ур-е прямой в пространстве

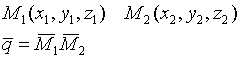
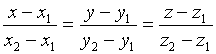- ур-е прямой прох. через 2 данные точки

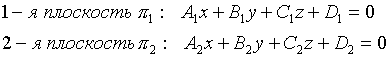
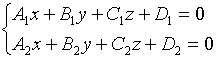- общее ур-е прямой в пространстве

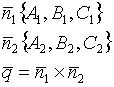
Пример.

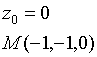
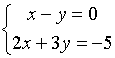
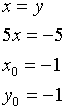
Условие параллельности 2-х прямых

; ;

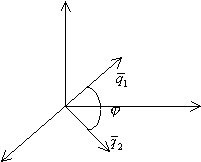
Если , то прямые перпендикулярны ортогонально.

назад | оглавление | вперёд