§ 4.4. Парабола
Параболой называется геометрическое место точек плоскости, расстояния которых от заданных на той же плоскости точки (фокуса параболы) и прямой (директрисы параболы) равны между собой.
Пусть точка F – фокус; прямая KL – директриса параболы; М – произвольная точка параболы.
По определению параболы:
(3.29),
где В – основание перпендикуляра, опущенного из точки М на директрису KL.
Введем обозначение 
,
где 
– основание перпендикуляра, опущенного из фокуса на директрису; величину 
,
расстояние от фокуса до директрисы, называют параметром параболы.
Для вывода простейшего
уравнения параболы оси координат расположим следующим образом: начало координат
поместим в точку О – середину отрезка 
;
за ось 
примем прямую, которой принадлежит отрезок ,
причем за положительное ее направление примем направление от точки О
к фокусу F;
ось 
направим перпендикулярно оси ,
т. е. параллельно директрисе.
При таком выборе осей координаты
фокуса 
будут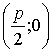 
,
а уравнение директрисы 
.
Для точки 
,
лежащей на параболе, имеем:
, 
;
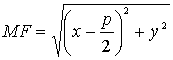подставляя эти значения в равенство (3.29), получаем:
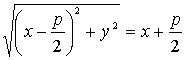(3.30).
Возведем обе части уравнения (3.30) в квадрат, одновременно раскрывая скобки:
.
Приводя подобные члены, получим простейшее (каноническое) уравнение параболы:
(3.31).
Построим параболу по этому уравнению.
Прежде всего отметим,
что вся парабола расположена справа от оси ;
в самом деле, в уравнении (3.31) левая часть неотрицательна (
),
в правой части 
;
следовательно, и второй множитель правой части неотрицателен: 
.
Поскольку в уравнение
(3.31) текущая координата 
входит только во второй степени, заключаем, что ось
является осью симметрии параболы. При 
и 
:
парабола проходит через начало координат; эту точку называют вершиной
параболы.
При возрастании 
одновременно возрастает и абсолютная величина 
,
ибо 
.
При построении параболы
полезно помнить, что ордината точки 
параболы, лежащей над ее фокусом, равна параметру параболы 
;
в самом деле, при 
из уравнения параболы (3.31) находим:
,
откуда
.
Таким образом, длина хорды 
параболы, проходящей через ее фокус перпендикулярно оси параболы, равна 
.
Если повернуть параболу
относительно осей координат на угол 
против часовой стрелки, то в уравнении (3.31) координаты 
и 
поменяются местами и уравнение такой параболы запишется так:
(3.32)
Вершиной этой параболы
по-прежнему является начало координат, но осью симметрии будет служить ось
;
парабола лежит над осью 
.
Фокусом этой параболы будет точка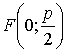 
;
директрисой – прямая 
(рис. 3.8).
Нетрудно далее убедиться в том, что уравнения:
(3.33)
и
(3.34)
(в обоих случаях 
)
также определяют параболы, которые от парабол, определяемых уравнениями (3.31)
и (3.32), отличаются только тем, что они направлены в сторону, противоположную
направлению соответствующих координатных осей: первая – вдоль отрицательной
оси ,
вторая – вдоль отрицательной оси .
Рекомендуем читателю самому найти координаты фокусов этих парабол и уравнения их директрис.
Уравнения парабол (3.31) и (3.33) можно записать в виде единого уравнения:
(3.31`),
а уравнения парабол (3.32) и (3.34) – в виде уравнения:
(3.32`),
если в уравнениях (3.31')
и (3.32')
рассматривать 
как коэффициент, принимающий и положительные, и отрицательные значения (параметр
параболы будет равен 
).
При 
парабола будет направлена в положительном направлении соответствующей оси
координат, а при 
– в отрицательном.