§ 4.3. Гипербола
Гиперболой называется геометрическое место точек плоскости, разность расстояний которых от двух данных точек той же плоскости, называемых фокусами гиперболы, постоянна.
Для вывода простейшего уравнения
гиперболы расположим оси координат по отношению к ее фокусам ![]() и
и ![]() так же, как мы это делали в предыдущем параграфе для эллипса. Сохраним для
гиперболы те же обозначения: 2а для постоянной величины, упоминаемой
в определении гиперболы, 2с
для расстояния между фокусами
так же, как мы это делали в предыдущем параграфе для эллипса. Сохраним для
гиперболы те же обозначения: 2а для постоянной величины, упоминаемой
в определении гиперболы, 2с
для расстояния между фокусами ![]() и
и ![]() .
Координаты фокусов те же, что и для эллипса в предыдущем параграфе:
.
Координаты фокусов те же, что и для эллипса в предыдущем параграфе: ![]() и
и ![]() .
.
Возьмем произвольную точку ![]() ,
лежащую на гиперболе. По определению гиперболы для точек кривой, лежащих в
I и IV
четвертях имеем:
,
лежащую на гиперболе. По определению гиперболы для точек кривой, лежащих в
I и IV
четвертях имеем:
![]() (3.18),
(3.18),
а для точек, лежащих во II и III четвертях:
![]() (3.18`).
(3.18`).
Заметим, что для гиперболы в отличие
от эллипса ![]() (2а
есть разность двух сторон треугольника
(2а
есть разность двух сторон треугольника ![]() ,
а 2с – его третья сторона). Выражая через координаты точек
,
а 2с – его третья сторона). Выражая через координаты точек ![]() ,
,
![]() и
и ![]() длины отрезков
длины отрезков ![]() и
и ![]() оба равенства (3.18) и (3.18')
можно записать в виде:
оба равенства (3.18) и (3.18')
можно записать в виде:
![]() (3.19).
(3.19).
Производя над этим уравнением те же преобразования, что и над уравнением (3.6) в случае эллипса (см. § 4.2), мы в конечном счете придем к тому же самому уравнению (3.10):
![]() ,
,
в котором, однако, теперь ![]() .
(Рекомендуется читателю произвести это преобразование самостоятельно.)
.
(Рекомендуется читателю произвести это преобразование самостоятельно.)
Деля левую и правую части уравнения
(3.10) на ![]() и учитывая, что теперь
и учитывая, что теперь ![]() ,
запишем результат в виде:
,
запишем результат в виде:
![]() (3.20).
(3.20).
Наконец, полагая ![]() ,
получим окончательно простейшее (каноническое) уравнение гиперболы:
,
получим окончательно простейшее (каноническое) уравнение гиперболы:
![]() (3.21).
(3.21).
Можно доказать, что равенство (3.21) равносильно объединенному равенству (3.19).
Для построению гиперболы по ее
уравнению (3.21) заметим прежде всего, что первый член левой части этого уравнения
не меньше его правой части, т. е. единицы (поскольку из ![]() вычитается неотрицательная величина
вычитается неотрицательная величина ![]() ):
):
![]() .
.
Отсюда ![]() .
Таким образом, в вертикальной полосе между параллельными оси Oy
прямыми
.
Таким образом, в вертикальной полосе между параллельными оси Oy
прямыми ![]() и
и ![]() точек кривой нет.
точек кривой нет.
Отмечаем далее, что, так же как и для эллипса, оси координат служат осями симметрии гиперболы, так как в уравнении (3.21) x и y входят лишь в четных степенях. Поэтому достаточно построить часть гиперболы, лежащую в I четверти.
Решим уравнение гиперболы (3.21)
относительно y: ![]() ,
выберем в правой части знак плюс, поскольку в I
четверти
,
выберем в правой части знак плюс, поскольку в I
четверти ![]() :
:
![]() ,
,
![]() (3.22).
(3.22).
При ![]()
![]() ;
при возрастании x
возрастает и y:
ветвь гиперболы, подымаясь от оси Ox,
уходит на плоскости все дальше и дальше, или, как говорят в геометрии, уходит
"в бесконечность". Но при этом, как нетрудно показать, ветвь кривой все ближе
и ближе подходит к прямой
;
при возрастании x
возрастает и y:
ветвь гиперболы, подымаясь от оси Ox,
уходит на плоскости все дальше и дальше, или, как говорят в геометрии, уходит
"в бесконечность". Но при этом, как нетрудно показать, ветвь кривой все ближе
и ближе подходит к прямой ![]() .
В самом деле, разность между ординатами точек этой прямой и гиперболы (обозначим
ее через
.
В самом деле, разность между ординатами точек этой прямой и гиперболы (обозначим
ее через ![]() ),
соответствующих одному и тому же значению абсциссы х, имеем следующее
выражение:
),
соответствующих одному и тому же значению абсциссы х, имеем следующее
выражение:
 (3.23)
(3.23)
Из последнего выражения видно,
что когда х неограниченно возрастает, то ![]() ,
оставаясь положительным, стремится к нулю, что и подтверждает высказанную
нами мысль: ветвь гиперболы, лежащая в I
четверти неограниченно приближается (и притом снизу, так как
,
оставаясь положительным, стремится к нулю, что и подтверждает высказанную
нами мысль: ветвь гиперболы, лежащая в I
четверти неограниченно приближается (и притом снизу, так как ![]() )
к прямой
)
к прямой ![]() ,
когда абсцисса х точки гиперболы неограниченно возрастает. Такие прямые,
к которым неограниченно приближаются уходящие в бесконечность ветви кривых,
называются асимптотами этих кривых.
,
когда абсцисса х точки гиперболы неограниченно возрастает. Такие прямые,
к которым неограниченно приближаются уходящие в бесконечность ветви кривых,
называются асимптотами этих кривых.
Таким образом, прямая ![]() является асимптотой гиперболы. В силу симметрии гиперболы у нее есть и вторая
асимптота:
является асимптотой гиперболы. В силу симметрии гиперболы у нее есть и вторая
асимптота: ![]() .
Наличие асимптот и соображения симметрии позволяют нам построить всю гиперболу
(рис. 5): кривая состоит из двух не смыкающихся ветвей, лежащих в углах между
прямыми
.
Наличие асимптот и соображения симметрии позволяют нам построить всю гиперболу
(рис. 5): кривая состоит из двух не смыкающихся ветвей, лежащих в углах между
прямыми ![]() и
и ![]() и неограниченно приближаются к этим прямым.
и неограниченно приближаются к этим прямым.
В отношении гиперболы используется следующая терминология.
Отрезок ![]() называют вещественной, а
называют вещественной, а ![]() – мнимой
осью гиперболы; их длины равны соответственно 2а и 2b
(а
– вещественная полуось, b
– мнимая полуось). Точки гиперболы
– мнимой
осью гиперболы; их длины равны соответственно 2а и 2b
(а
– вещественная полуось, b
– мнимая полуось). Точки гиперболы ![]() и
и ![]() ,
лежащие на вещественной оси, – вершины гиперболы. Точка О
– центр
гиперболы. Изображенный на рис. 3.5 пунктиром прямоугольник
,
лежащие на вещественной оси, – вершины гиперболы. Точка О
– центр
гиперболы. Изображенный на рис. 3.5 пунктиром прямоугольник ![]() с центром в точке О и сторонами
с центром в точке О и сторонами ![]() ,
и
,
и ![]() ,
параллельными осями симметрии гиперболы, называют осевым прямоугольником
гипербол; его построение облегчает построение гиперболы; сама гипербола касается
вертикальных сторон этого прямоугольника в их серединах, являющихся вершинами
гиперболы.
,
параллельными осями симметрии гиперболы, называют осевым прямоугольником
гипербол; его построение облегчает построение гиперболы; сама гипербола касается
вертикальных сторон этого прямоугольника в их серединах, являющихся вершинами
гиперболы.
Для построения фокусов гиперболы
![]() и
и ![]() полезно знать, что основное соотношение между величинами
полезно знать, что основное соотношение между величинами ![]() ,
,
![]() и
и ![]() у гиперболы можно записать в виде:
у гиперболы можно записать в виде:
![]() (3.24).
(3.24).
Поэтому расстояние от центра гиперболы
до ее фокуса ![]() равно половине длинны диагонали осевого прямоугольника
равно половине длинны диагонали осевого прямоугольника ![]() :
в прямоугольном треугольнике
:
в прямоугольном треугольнике ![]() катеты
катеты ![]() ,
,
![]() ,
а следовательно, его гипотенуза
,
а следовательно, его гипотенуза ![]() .
.
Форма гиперболы зависит от угла
наклона асимптоты к вещественной оси, т. е. от величины отношения ![]() :
чем эта величина меньше, тем меньше угол между асимптотами, в котором заключена
гипербола, и тем более сжата сама гипербола; чем больше величина
:
чем эта величина меньше, тем меньше угол между асимптотами, в котором заключена
гипербола, и тем более сжата сама гипербола; чем больше величина ![]() ,
тем круче располагаются ветви гиперболы.
,
тем круче располагаются ветви гиперболы.
Но, так же как и для эллипса,
в качестве характеристики формы гиперболы в аналитической геометрии пользуются
не величиной отношения ![]() ,
а величиной
,
а величиной ![]() ,
называемой эксцентриситетом гиперболы и обозначают той же буквой
,
называемой эксцентриситетом гиперболы и обозначают той же буквой ![]() ,
как и для эллипса:
,
как и для эллипса:
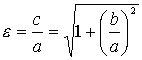 (3.25).
(3.25).
Так как у гиперболы ![]() ,
то эксцентриситет гиперболы
,
то эксцентриситет гиперболы ![]() .
Из прямоугольного треугольника
.
Из прямоугольного треугольника ![]() , в котором острый угол наклона асимптоты к вещественной оси обозначен через
, в котором острый угол наклона асимптоты к вещественной оси обозначен через
![]() ,
находим:
,
находим:
![]()
и, следовательно:
![]() (3.26),
(3.26),
т. е. эксцентриситет гиперболы
![]() равен секансу угла наклона асимптоты к вещественной оси.
равен секансу угла наклона асимптоты к вещественной оси.
Важным частным случаем гиперболы
является равносторонняя (равноосная) гипербола – такая гипербола, у
которой равны длины вещественной и мнимой полуосей: ![]() .
.
Уравнение этой гиперболы имеет вид:
![]() (3.27).
(3.27).
У равносторонней гиперболы, как
нетрудно показать, угол между асимптотами прямой, ![]() и
и ![]() .
.
Для гиперболы, у которых оси совпадают и равны, но вещественная ось одной служит мнимой осью другой и наоборот, называются сопряженными; асимптоты таких гипербол также совпадают (поскольку совпадают их осевые прямоугольники), но гиперболы располагаются в смежных углах между асимптотами.
Нетрудно видеть, что если уравнением одной из сопряженных гипербол является уравнение (3.21):
![]() ,
,
то уравнение второй будет иметь вид:
![]() ,
или
,
или ![]() (3.28),
(3.28),
поскольку меняются ролями оси Ox и Oy и полуоси гипербол а и b.
Отметим, что расстояние с
от центра до фокусов у обеих сопряженных гипербол одно и то же, определяемое
формулой (3.24), но эксцентриситеты различные: ![]() ,
,
![]() ;
;![]() (если только обе гиперболы не являются равносторонними).
(если только обе гиперболы не являются равносторонними).