§ 4.2. Эллипс
Эллипсом называется геометрическое место точек плоскости, сумма расстояний которых от двух данных точек этой же плоскости, называемых фокусами эллипса, постоянна.
Пусть фокусами эллипса являются точки F1 и F2 , а М – некоторая точка, принадлежащая эллипсу. По определению эллипса для любой его точки М имеем:
(3.4)
где через 
обозначена упоминаемая в определении эллипса постоянная величина. Введем обозначение
;
очевидно, что 
(
– сумма двух сторон треугольника 
,
а 
– его третья сторона).
Для вывода простейшего
уравнения эллипса выберем следующее расположение координатных осей. Начало
координат О поместим в середину отрезка 
,
а за ось 
примем прямую, проходящую через фокусы 
и 
,
ось 
направим перпендикулярно к оси
в точке 
.
При таком выборе осей
координаты фокусов будут 
,
;
произвольную точку эллипса обозначим через 
.
Имеем:
,
(3.5),
а подставляя эти значения в уравнение (3.4), находим:
(3.6).
Получено уравнение эллипса. Для преобразования уравнения к более простому виду перенесем корень второй степени в правую часть равенства и возведем обе части равенства в квадрат (одновременно раскрыв скобки):
(3.7).
Перенося в этом уравнении радикал в левую часть, а все остальные члены – в правую часть равенства, после привидения подобных членов и сокращения на общий множитель найдем:
(3.8).
Снова возведем в квадрат обе части уравнения:
(3.9).
Перенесем теперь члены с текущими координатами в левую часть равенства, а постоянные члены – в правую:
(3.10).
Наконец,
разделим левую и правую части на 
:
(3.11).
Так как 
,
то можно положить 
;
тогда окончательно получим следующую простейшую (ее называют канонической)
форму уравнения эллипса:
(3.12).
Можно доказать, что уравнение (3.12) равносильно исходному уравнению (3.6).
Исследуем форму эллипса по его уравнению. Прежде всего заметим, что каждое из двух слагаемых левой части уравнения (3.12) не превосходит единицы, поскольку их сумма (а они оба положительны) равна единице:
, 
;
отсюда найдем, что для всех точек эллипса:
,
,(3.13)
т. е. что эллипс целиком лежит внутри прямоугольника, определяемого неравенствами (3.13).
Далее заметим, что уравнение (3.12)
сохраняет вид, если заменить 
на 
или 
на 
(поскольку x и
y входят в уравнение
лишь во второй степени). Из этого следует, что если на эллипсе лежит некоторая
точка 
,
то одновременно с нею на эллипсе лежат и три точки 
,
и 
,
симметричные с точкой М соответственно относительно оси Ox
, оси Oy и начала
координат. Это означает, что эллипс имеет оси координат своими осями симметрии
и поэтому для его построения достаточно построить его дугу, лежащую, например,
в I четверти.
Решим уравнение (3.12) относительно y:
(3.14).
Для построения дуги эллипса, лежащей в I четверти, надо в правой части (3.14) взять знак плюс и изменять x только от 0 до a:
,
(3.14`)
Из этого уравнения следует:
1) при 
;
2) при возрастании x
от 0 до а y
убывает от b
до 0; 3) при 
.
Это позволяет нам построить дугу эллипса, лежащую в I
четверти, и по соображениям симметрии весь эллипс.
Познакомимся с принятой в аналитической геометрии по отношению к эллипсу терминологией.
Отрезки 
и 
осей симметрии эллипса, принятых нами з оси координат, называют соответственно
большой и малой осями эллипса; их длины равны соответственно
2a и 2b
(
, так
как 
);
половину их длин – числа a
и b – часто называют
большой и малой полуосями эллипса. Точка О пересечения осей
симметрии эллипса называется его центром. Концы большой и малой осей
эллипса – точки 
,
, 
,
– называют его вершинами.
Форма эллипса зависит
от величины соотношения 
длин его малой и большой полуосей: чем больше это соотношение, тем эллипс
будет менее "сплющенным", менее сжатым; при 
эллипс, как легко установить по его уравнению (3.12), превращается в окружность;
в самом деле, в этом случае уравнение (3.12) превращается в уравнение:
(3.15),
т. е. в уравнение окружности радиуса а с центром в начале координат.
В качестве характеристики
формы эллипса в аналитической геометрии чаще пользуются не соотношением его
полуосей ,
а другой величиной – отношением половины расстояния с между фокусами
эллипса к его большой полуоси а, которое называют эксцентриситетом
и обозначают греческой буквой "эпсилон" (
):
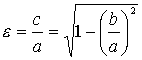(3.16).
Так как 
,
то эксцентриситет для различных эллипсов может меняться в пределах от 0 до
1: 
;
чем больше эксцентриситет, тем больше расстояние от центра эллипса до его
фокусов и тем более сплющен эллипс; чем ближе эксцентриситет к нулю, тем больше
форма эллипса приближается к окружности. (Если положить 
,
то эллипс превращается в окружность; если положить 
,
эллипс превращается в свою собственную большую ось.)
Если по уравнению эллипса
(3.12) нужно построить не только сам эллипс, но и отметить на чертеже положение
его фокусов 
и 
,
то полезно запомнить. Что расстояния от фокусов эллипса до концов 
и 
его малой оси равны длине большой полуоси эллипса а:
.
Это сразу следует мз основного соотношения, связывающего величины a, b и с:
(3.17).
Пример.
Найти простейшее уравнение
и построить его, если его большая ось расположена на оси Ox
симметрично относительно начала координат и имеет длину 
,
а эксцентриситет эллипса 
.
Решение. Пользуясь формулой (3.16), находим с:
.
Затем по формуле (3.17)
определяем 
.
Зная теперь a
и b,
получаем простейшее уравнение эллипса:
.
Построение этого эллипса по его уравнению рекомендуем читателю сделать самостоятельно.
Рассмотрим теперь уравнение
,
в котором 
.
Очевидно, отнесенный
к системе координат, в которой оси Ox
и Oy
поменялись ролями: большая ось и фокусы этого эллипса лежат на оси Oy,
а малая ось – на оси Ox
(рис. 3.3). Следует лишь помнить, что для такого эллипса 
и 
.
Координаты фокусов такого эллипса: 
и 
.