N – натуральные числа,

Q – рациональные(дробные),

Z – целые числа,

R – действительные числа;

– счетные и имеют одинаковую мощность

R – несчетное множество.

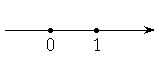Множество действительных чисел всюду плотно на числовой оси.

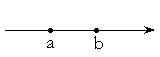[a, b] – замкнутый интервал,   (a, b) – открытый интервал

Окр [x₀] = (a, b), где (a, b) содержит x₀ – это окрестность.

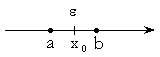ax₀ = x₀b, – окрестность x₀

Кванторы

1) – кванты всеобщности;

2) – кванты существования.

|x – x₀| – расстояние от точки x до точки x₀

Числовой функцией называется соответствие между числовыми множествами XY, при котором каждому значению x соответствует (сопоставлено) некоторое значение y.

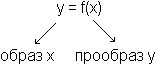
У каждого прообраза всегда один образ, у каждого образа может быть много прообразов.

Взаимнооднозначная функция – это когда разные x имеют разные y.

1. Элементарные
2. Неэлементарные (специальные).

Элементарные функции изучаются в школьной математике и делятся на:

1. Основные элементарные функции

а) степенные y = xⁿ

б) показательные y = a^x

в) тригонометрические y = sin x и другие.

2. Элементарные, полученные из основных с помощью арифметических операций и операции получения сложной функции (операции композиции).

   f

   

   X          Y         

   

   f ^-1 (обратная функция)

   Обратные к показательным функциям – логарифмические функции. Обратные к тригонометрическим

   Пример:

   

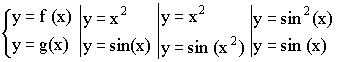
   y = f (g(x)) – сложная функция – композиция элементарных функций.

   

Элементарными функциями называются функции, полученные из элементарных базисных функций с помощью алгебраических операций и операций композиции.

Г(f) – график функции. График функции есть множество точек (x, y), где y = f(x).

1. Четность –
2. Нечетность –
3. Периодичность –

назад | оглавление | вперёд