– окрестности точки b существует 
– окрестность точки а.|
Математический анализ |
|
Тема 1. Введение в анализ.Теория пределов. |
назад | оглавление | вперёд |
1.3. ПРЕДЕЛ ФУНКЦИИ. СВОЙСТВА ПРЕДЕЛОВ
Число b называется пределом функции
в точке а, если для любой
– окрестности точки b существует
– окрестность точки а.
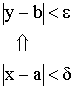
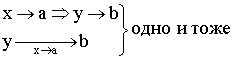
– предел функции при 
,
равный b.
Число b
называется пределом функции при неограниченном
возрастании аргумента 
.
Для любого 
существует
такое N,
и если 
,
то 
.
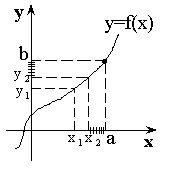
Примеры:
y = f(x) = 
y = f(x) = x2 
Пример:
y =
,
когда 
,
Неопределенности: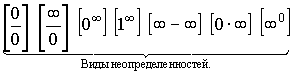 
Раскрытие неопределенностей.
Теорема об ограниченности функции, имеющей предел.
Если функция f(x)
имеет предел в точке a
,то
она ограниченна в некоторой окрестности точки a.
Доказательство:
Пусть ,
тогда 
,
отсюда получаем 
.
Обратное неверно.
Контрольный пример:
в окрестности точки 0.
– не существует.
Бесконечно малой величиной
при
называется функция, предел которой в точке a
равен 0.
–
бесконечно малая величина (б.м.в.).
– бесконечно малая величина при 
– бесконечно малая величина при 
s
Бесконечно большой величиной
при
называется функция неограниченно возрастающая.
– бесконечно большая величина (б.б.в.)
Любая бесконечно большая величина неограниченна.
Теорема о связи предела и бесконечно малой величины.
Если 
,
то 
,
где 
– бесконечно малая величина. Или 
.
Доказательство:
Допустим, что ,
тогда 
.
,
значит 
,
– бесконечно
малая величина.
Пример:
f(x) = x2 + 1
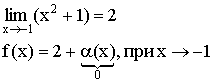
Теорема о связи бесконечно малой и бесконечно большой величиной.
Если 
– бесконечно малая величина при
– бесконечно большая величина.
Если 
–
бесконечно большая величина при
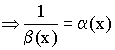– бесконечно малая величина.
Доказательство:
Допустим, что
– бесконечно малая величина при ,
то 
,
что 
.
Значит 
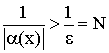
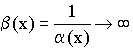
Следствие: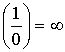 
и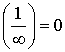 
Свойства бесконечно малых величин:
1) Алгебраическая сумма бесконечно
малых величин есть бесконечно малая: 
Доказательство:
или 
,
значит 
– бесконечно малая величина.
2) Произведение бесконечно малой
величины на ограниченную функцию есть бесконечно малая: 
,
где f(x)
– ограниченная.
Доказательство:
,
значит 
– бесконечно малая величина.
3) Частное от деления бесконечно малой величины
на любую функцию, предел которой не равен 0, есть бесконечно малая: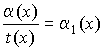 
при 
и 
.
Теоремы о пределах.
Теорема 1. Предел
суммы равен сумме пределов, если они существуют: 
Доказательство:
Из теоремы о связи между пределом и бесконечно малой величиной следует:
Получаем 
Теорема 2. Предел
произведения равен произведению пределов, если они существуют: 
Доказательство:
Из теоремы о связи между пределом и бесконечно малой величиной следует:
Получаем 
Теорема 3. Предел
частного равен частному пределов: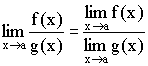 
.
При условии: все пределы существуют и 
.
Доказательство:
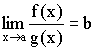
Из теоремы о связи между пределом и бесконечно малой величиной следует:
;
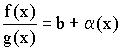
Получаем: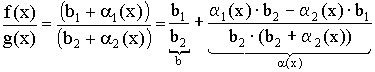 
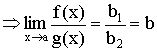
Теорема 4. Предел
сохраняет знак неравенства. Если 
.
Доказательство:
Следовательно,
Следствие:
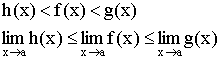
Теорема 5. Если
функция ограниченна и монотонна на (a,
b), то она имеет предел: 
Теорема 6. Критерий Коши.
Если 
,
тогда и только тогда 
.
Приемы раскрытия неопределенностей.
1) Выделение общего множителя (для
неопределенности 
).
Пример:
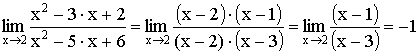
2) Умножение на сопряженное выражение
(для неопределенности ).
Пример:
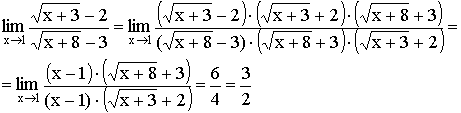
3) Выделение главной части (для
неопределенности 
).
Примеры:
;
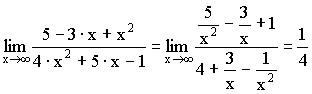
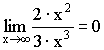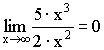
Теорема. Первый
замечательный предел 
.
Доказательство (геометрическое):
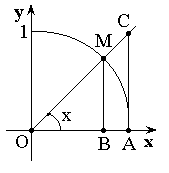
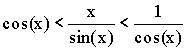
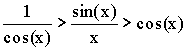
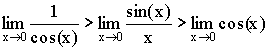
Так как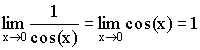 
,
то 
.
Следствия из теоремы:
1) 
2) 
3) 
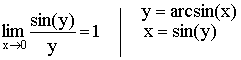
4) 
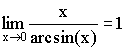
5) 
Теорема. Второй
замечательный предел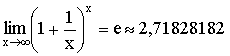 
.
Доказательство:
Бином Ньютона:
,
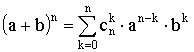где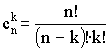 
.
Используем бином Ньютона для доказательства
неравенства: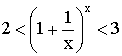 
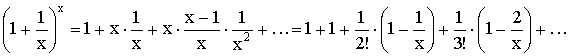
Отсюда заключаем, что ,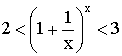
а значит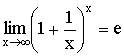 
.
Следствия из теоремы:
1) 
2) 
3)
4) 
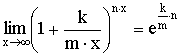
Доказательство:
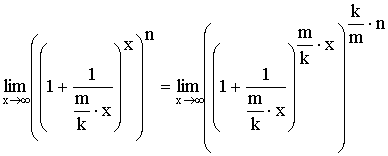
Если принять, что 
,
то 
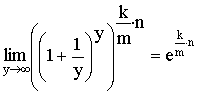
Примеры:
1) 
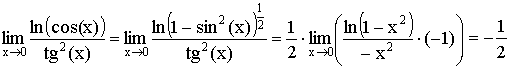
Учитывая, что 
.
2) 
.
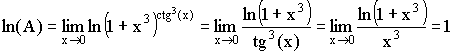Отсюда A = e.
Учитывая, что 
.
Сравнение бесконечно малых величин (б.м.в.):
Пусть 
– бесконечно малые величины при 
,
т.е. 
.
Определение 1.
Если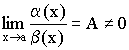 
,
то
– б.м.в. одного порядка малости.
Определение 2.
Если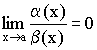 
,
то 
– б.м.в. более высокого порядка, чем .
– 
более высокого порядка, чем 
("о" – читается как "о малое").
–
более низкого порядка, чем
("О" – читается как "О большое").
Определение 3.
Если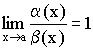 
,
то 
и
эквивалентны – 
.
Следствие из определения
3: 
при 
.
Теорема. Если
и
эквивалентны (
)
, то 
и 
.
Доказательство:
Пусть
– бесконечно малые величины при
и они эквивалентны ().
Тогда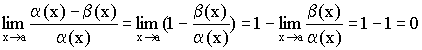 
.
назад | оглавление | вперёд