1.4. НЕПРЕРЫВНОСТЬ ФУНКЦИИ В ТОЧКЕ И НА ИНТЕРВАЛЕ
Определение 1.
Пусть функция ![]() определена в окрестности точки
определена в окрестности точки ![]() ,
тогда функция непрерывна в
,
тогда функция непрерывна в ![]() ,
если
,
если ![]() .
.
Определение 2.
Функция ![]() непрерывна, если
непрерывна, если![]() .
.
Определение 3.
Функция ![]() непрерывна в точке
непрерывна в точке ![]() ,
если
,
если ![]() .Приращение
аргумента
.Приращение
аргумента ![]() .
Приращение функции
.
Приращение функции ![]() .
.
Определение 4. Функция ![]() непрерывна в точке
непрерывна в точке ![]() ,
если
,
если ![]() .
Если функция не является непрерывной в точке
.
Если функция не является непрерывной в точке ![]() ,
то эта точка – точка разрыва. Если функция непрерывна на отрезке (a, b), то
функция неразрывна на отрезке (a, b).
,
то эта точка – точка разрыва. Если функция непрерывна на отрезке (a, b), то
функция неразрывна на отрезке (a, b).
Определение 5.
Функция ![]() непрерывна в точке
непрерывна в точке ![]() справа, если
справа, если ![]() .
.
Определение 6.
Функция ![]() непрерывна в точке
непрерывна в точке ![]() слева, если
слева, если ![]() .
.
Функция непрерывна на отрезке
![]() ,
если она непрерывна в каждой внутренней точке этого отрезка и односторонне
непрерывна на его концах.
,
если она непрерывна в каждой внутренней точке этого отрезка и односторонне
непрерывна на его концах.
Теоремы о непрерывных функциях.
Теорема 1. Сумма, произведение и частное непрерывных функций – непрерывны (кроме случая, когда знаменатель обращается в нуль).
Доказательство:
Пусть ![]() и
и ![]() .
.
Тогда ![]() .
.
Доказательство для умножения и деления аналогично доказательству для сложения.
Теорема 2. Композиция непрерывных функций непрерывна:
Функция ![]() непрерывна в точке
непрерывна в точке ![]() ,
если g(x) непрерывна в точке
,
если g(x) непрерывна в точке ![]() и
f(y) непрерывна в
и
f(y) непрерывна в ![]() .
.
Теорема 3. Все элементарные функции непрерывны в своей области определения.
Разрывы функции.
Разрыв первого рода.
Пусть ![]() и
и ![]() существуют:
существуют:
I. Если
![]() ,
то в точке
,
то в точке ![]() функция
испытывает разрыв скачок первого рода.
функция
испытывает разрыв скачок первого рода.
Примеры:
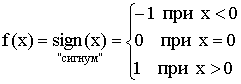
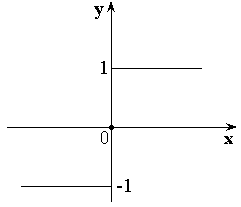
-
 – целая часть числа x.
– целая часть числа x.
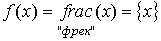 – дробная часть от числа
x.
– дробная часть от числа
x. 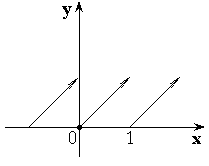
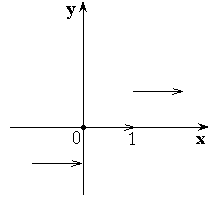
II. Если
![]() , то
в точке
, то
в точке ![]() функция
испытывает устранимый разрыв первого рода.
функция
испытывает устранимый разрыв первого рода.
Примеры:
1) 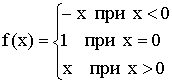
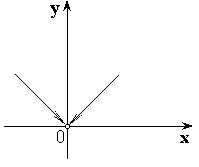
2) 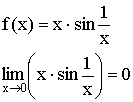
3) 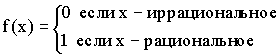
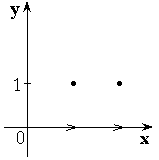
4) 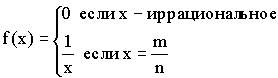
Разрыв второго рода.
Функция испытывает разрыв второго
рода, если ![]() – не существует.
– не существует.
Свойства функции, непрерывной на замкнутом отрезке.
Пусть функция ![]() непрерывна на замкнутом отрезке
непрерывна на замкнутом отрезке ![]() .
.
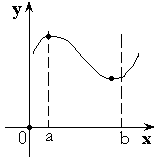
Теорема 1.
Функция принимает наибольшее и наименьшее значение на ![]() .
Или
.
Или ![]() ,
где
,
где ![]() .
.
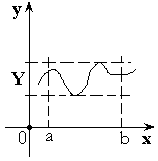
Теорема 2. Функция принимает все свои промежуточные
значения на ![]() .
Или
.
Или ![]() ,
где
,
где ![]() – область значений.
– область значений.
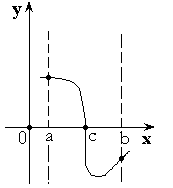
Теорема 3.
Если функция принимает на концах отрезка ![]() значения разных знаков, то внутри отрезка найдется точка, в которой
значения разных знаков, то внутри отрезка найдется точка, в которой ![]() .
Или
.
Или ![]() .
.