определенна в окрестности точки 
.|
Математический анализ |
|
Тема 2. Дифференциальное исчисление. |
назад | оглавление | вперёд |
2.1. ПРОИЗВОДНАЯ ФУНКЦИИ. ЕЁ ФИЗИЧЕСКИЙ И ГЕОМЕТРИЧЕСКИЙ СМЫСЛ.
Пусть функция
определенна в окрестности точки .
Тогда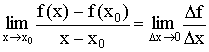 
,
где 
и 
.
Производная функции в точке есть предел отношения
приращения функции (
)
и приращения аргумента (
),
когда 
.
Дифференцируемость.
Механический смысл производной.
Производная – это скорость изменения функции.
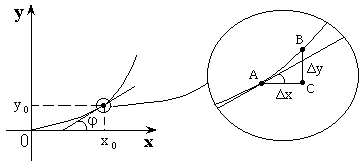
Геометрический смысл производной.
Производная – это тангенс наклона
угла касательной к график функции в данной точке к оси 
.
;
при 
Вычисление производной.
Теорема. Если функция дифференцируема в точке, то она непрерывна в этой точке.
Доказательство:
при
при 
,
следует 
Обратное неверно.
Пример:
1) 
; 
; 
; 
;
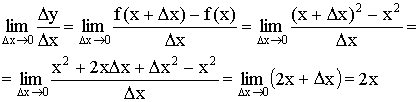
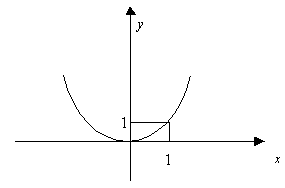
Таблица производных.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
назад | оглавление | вперёд
