Математический анализ  

Тема 2. Производная функции.

назад | оглавление | вперёд

2.2. ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ.

1) Производная от суммы равна сумме производных:

Доказательство:

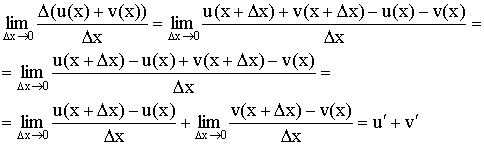
2) Постоянный множитель выносится за знак производной: .

3) Производная произведения: .

Доказательство:

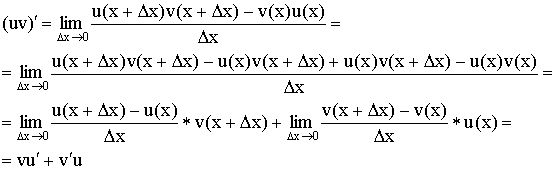
4) Производная дроби: .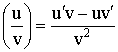

Доказательство:

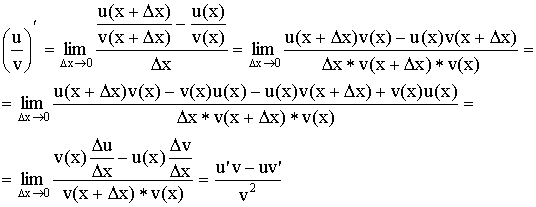
Вывод формул для производных.

1)

2)

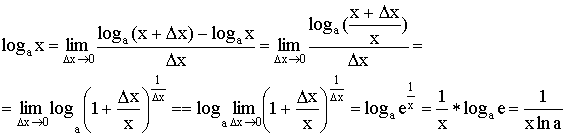
3)

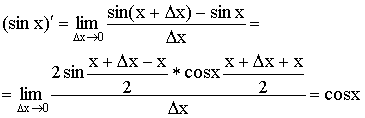
4)

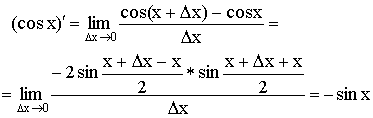
5)

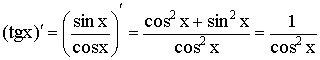
6)

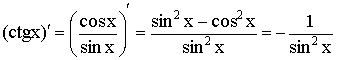
7)

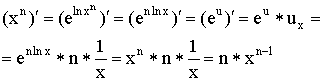
8)

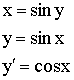
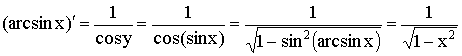
9)

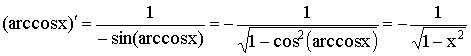
10)

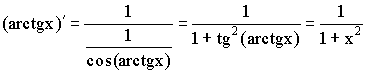
11)

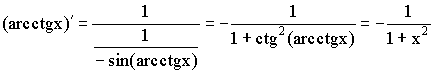
Теорема о производной сложной функции.

Теорема.

Доказательство:

Пусть , определена и непрерывна в окрестности точки (, определена и непрерывна в окрестности точки . Тогда .

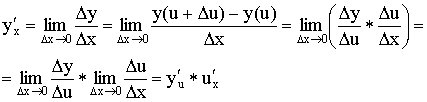
Это верно при условии, что каждая из функций дифференцируема.

Теорема о производной обратной функции.

Теорема.

Доказательство:

Пусть дифференцируемая в точке (). - обратная к . Обратная функция существует если монотонная функция. Тогда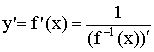

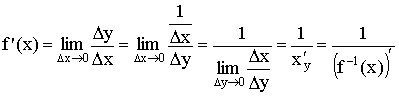
Производная сложной степенной функции.

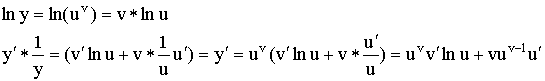
Прием логарифмического дифференцирования.

Производная неявной функции.

– общий вид неявно заданной функции.

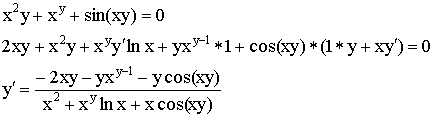
Производная параметрически заданной функции.

Примеры параметрических функций:

1)   

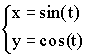
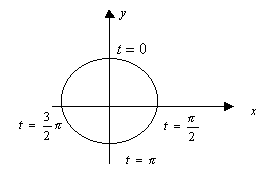
2)

3)

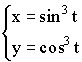
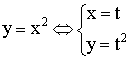
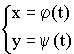
    – дифференцируемы.

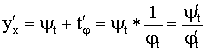
Пример:

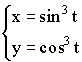
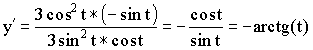
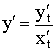
Гиперболические функции.

(гиперболический синус)

arsh x (ареа синус)

(гиперболический косинус)

 arсh x (ареа косинус)

(гиперболический тангенс)

arth x (ареа тангенс)

(гиперболический котангенс)

arcth x (ареа котангенс)

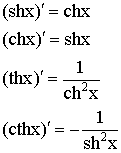
Схематичные графики гиперболических функций:

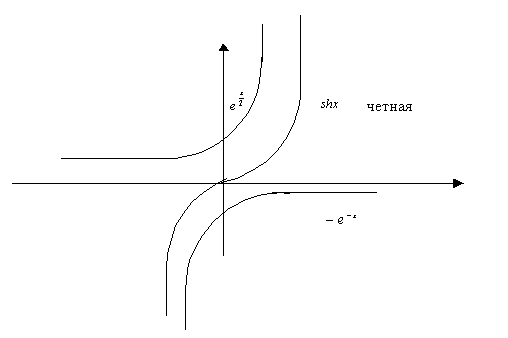
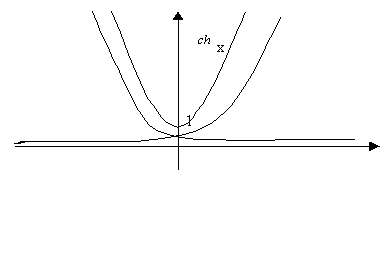
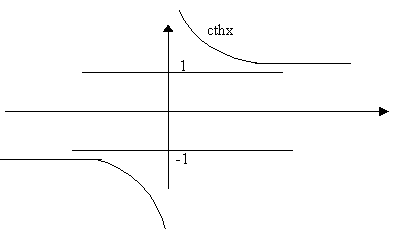
Производные высших порядков.

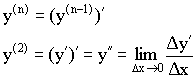
Механический смысл второй производной – это ускорение.

Геометрический смысл второй производной – отвечает за вогнутость или выпуклость графика функции.

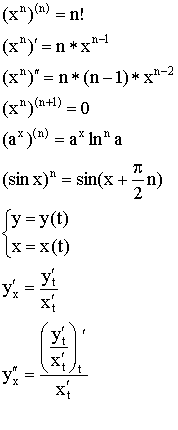
назад | оглавление | вперёд