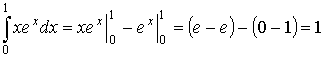3.4. Понятие определенного интеграла и его вычисление.
Определение и свойства.
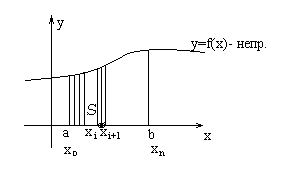
S – область – криволинейная трапеция.
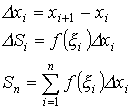
Интегральная сумма: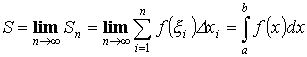
Определенным интегралом называется предел интегральной суммы.
Т. “О существовании определенного интеграла”.
Если f(x) – непрерывна на отрезке (a,b), то определе нный интеграл существует и не зависит от порядка разбиения и выбора точек.
Геометрический смысл определенного интеграла – площадь криволинейной трапеции.
Свойства определенного интеграла:
-
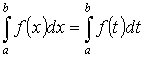
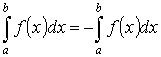
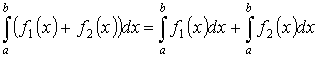
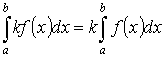
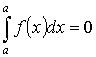
- аддитивность.
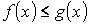на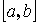 
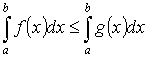
Основные теоремы интегрального исчисления.
Т.1. “об оценке”:
Пусть y =f(x) интегрируема на [a ,b] 
Тогда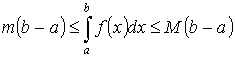 
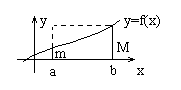
Доказательство:
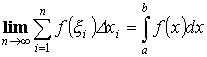
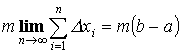
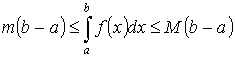
Т.2. “о среднем”
Пусть y =f(x) интегрируема на [a ,b] Тогда
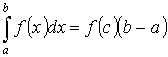- где 
f(c)
– среднее значение f(x) на
[a ,b].
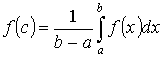
Доказательство:
По Т.1: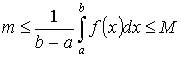
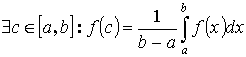
Т.к. f(x) – непрерывна на [a ,b], то она принимает
все промежуточные значения от m до M. Следовательно она принимает значение
А. Т.е. существует такая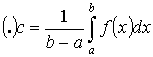 
Т.3. “о производной определенного интеграла по переменному верхнему пределу”
Пусть y =f(x) - интегрируема на [a , b]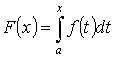
. Тогда 
Доказательство:
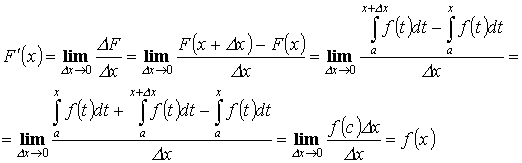
Т.4. “формула Ньютона-Лейбница”
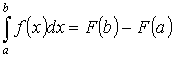, где F(x)
– первообразная для f(x).
Доказательство:
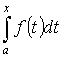- первообразная
для f(x) по Т.3. Т.к. первообразные отличаются
на const, то 
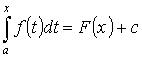Пусть
х=а. F(a)+c=0.
c=-F(x). Пусть
x=b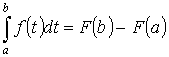 
Методы вычисления определенного интеграла.
Замена переменных под знаком определенного интеграла.
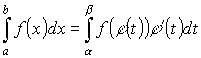
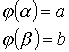
Пример:
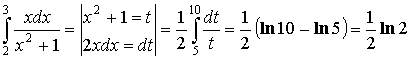
Интегрирование по частям в определенном интеграле.
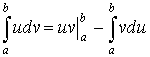
Пример:
