Теория электрических цепей

Основные сведения из теории фильтрующих цепей

назад | оглавление | вперёд

2. Основные сведения из теории фильтрующих цепей

Электрические фильтры – это линейные четырехполюсники, обладающие избирательными свойствами: они предназначены для выделения из состава сложного электрического колебания частотных составляющих определенного спектра частот, лежащего в полосе пропускания (ПП), и подавления тех составляющих, частоты которых лежат за пределами ПП, т. е. в полосе непропускания (ПН) или полосе задерживания (ПЗ). Между этими полосами находится переходная область. На рис. 2.1 приведены структурные характеристики ослабления фильтра нижних частот (ФНЧ) и полосового фильтра (ПФ). Для ФНЧ полоса пропускания лежит в диапазоне частот 0 ¸ f_п, а непропускания – в диапазоне f_з ¸ ¥ (рис. 2.1, а); для ПФ полоса пропускания f_п1 ¸ f_п2 располагается между полосами непропускания 0 ¸ f_з1 и f_з2 ¸ ¥ (рис. 2.1, б).

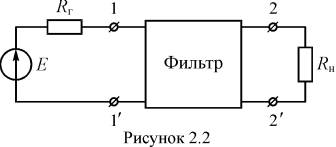
Требования к электрическим характеристикам фильтров задаются в виде допустимых пределов изменения этих характеристик. Так ослабление в ПП не должно превышать максимально допустимого ослабления А_max = DА, а в ПН не должно быть ниже значения А_min. Требования к другим характеристикам фильтров здесь не рассматриваются. Схема подключения фильтра к источнику сигнала приведена на рис. 2.2.

Синтез (расчет) фильтров состоит из двух этапов: этапа аппроксимации и этапа реализации. На первом этапе по заданным А_min и А_max в ПП и ПН формируется передаточная функция фильтра, т. е. математическое описание цепи, которая удовлетворяет указанным выше требованиям. На втором этапе создают схему цепи и определяют значения ее элементов по полученной передаточной функции.

Оба этапа хорошо разработаны применительно к синтезу ФНЧ. Что касается синтеза других типов фильтров: полосовых, заграждающих (режекторных), фильтров верхних частот, – то возможны различные варианты расчета. Один из них основан на том, что требования к заданному фильтру пересчитываются в требования к его НЧ-прототипу на основании принципа преобразования частоты. Рассчитывается НЧ-прототип по методике синтеза ФНЧ. Затем полученная схема НЧ-прототипа преобразуется в схему заданного фильтра, но только в случае пассивных фильтров [1¸3,5¸7]. В случае активных фильтров этап реализации осуществляется другим методом.

 

2.1. Синтез пассивных полосовых фильтров

Этап аппроксимации. Задано: частоты f_п1 и f_п2 – границы ПП и частота f_з2 – граница ПН справа; ослабление А_min и А_max = DА (рис. 2.1, б). Используя понятие центральной частоты или средней геометрической частоты ПП и ПН

                                                                         (2.1)

находим значение f_з1 – граничной частоты ПН слева.

Требования к характеристикам ПФ пересчитываются в требования к его НЧ-прототипу:

                                                             (2.2)

при тех же значениях А_min и А_max (рис. 2.1, а).

Зная требования к ослаблению ФНЧ можно пересчитать их в требования к АЧХ ФНЧ или, как это принято в теории фильтров, в требования к квадрату АЧХ |H(j2pf)|² = |H(jw)|². Для унификации расчетов вместо угловой частоты w вводят понятие нормированной частоты W = w/w_н, где w_н – нормирующая частота. Обычно в качестве w_н выбирают граничную частоту ПП ФНЧ. Тогда

                                                                   (2.3)

При синтезе ФНЧ используются универсальные соотношения [1,5]:

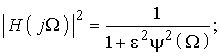                                                                         (2.4)

                                                                     (2.5)

где y(W) – функция фильтрации; e – коэффициент неравномерности ослабления в ПП. Если в качестве y(W) используются полиномы, то фильтры называются полиномиальными. Среди последних наиболее широкое применение нашли фильтры Баттерворта и Чебышева.

У фильтров Баттерворта y(W) = В_m(W) = W^m, где m – порядок фильтра. Характеристика H²(W) = |H(jW)|², т. е. квадрата коэффициента передачи для таких фильтров разного порядка m приведена на рис. 2.3, а (кривая 1 – характеристика идеального ФНЧ, кривая 2 для m = 6, кривая 3 для m = 2). При W = 1 все кривые проходят через точку, зависящую от e. Из анализа рисунка видно, что e действительно определяет неравномерность коэффициента передачи ФНЧ в ПП.

Если в (2.4) положить y(W) = В_m(W), а jW = р, то после преобразований получим передаточную функцию фильтра в виде

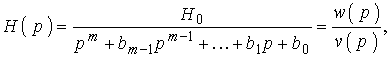                                       (2.6)

где H₀ = 1/e.

У фильтров Чебышева функция фильтрации y(W) = Т_m(W) = = cosm× arccosW для области нормированных частот –1 Ô W Ô 1. Характеристика квадрата коэффициента передачи при разных m показана на рис. 2.3, б (кривая 1 – характеристика идеального ФНЧ, кривая 2 для m = 4, кривая 3 для m = 2). Анализ кривых на рис. 2.3, б показывает, что полином Чебышева в интервале 0 Ô W Ô 1 принимает экстремальные значения (min или max) m + 1 раз. Или по иному: порядок фильтра нижних частот Чебышева по кривой H²(W), или по любой другой частотной характеристике фильтра, определяется удвоенным количеством периодов колебаний в ПП, рассчитанном на уровне полосы пропускания. На рис. 2.3, б: граница полосы пропускания по частоте – это W = 1; уровень полосы пропускания – это 1/(1 + e²).

Передаточная функция фильтра Чебышева описывается тем же выражением (2.6), но коэффициент H₀ = 1/(e×2^m–1).

Анализ кривых на рис. 2.3 показывает, что:

–       чем выше порядок фильтра, тем выше его избирательность за счет уменьшения переходной области;

–       при одинаковом порядке m избирательность фильтров Чебышева выше избирательности фильтров Баттерворта;

–       у фильтров Чебышева ФЧХ в полосе пропускания имеет нелинейный характер за счет волнового характера изменения Н²(W) в ПП.

Итак, этап аппроксимации при синтезе ПФ заканчивается получением функции H(p) для НЧ-прототипа.

Этап реализации. Если фильтр со стороны зажимов 1–1¢ рассматривать как двухполюсник, образованный реактивным четырехполюсником и нагрузкой R_н (рис. 2.2), то, можно оперировать понятием входного сопротивления Z_вх.1(р) двухполюсника со стороны зажимов 1–1¢:

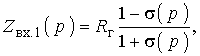                                                                             (2.7)

где s(р) – коэффициент отражения, характеризующий несогласованность между сопротивлениями R_г и Z_вх.1(р). Если известно Z_вх.1(р), то двухполюсник можно реализовать, например, методом Дарлингтона [1, 2, 3, 5, 6]. Один из возможных вариантов реализации схемы названным методом сводится к следующему. Осуществляют нормирование Z_вх.1 по сопротивлению, выбирая в качестве нормирующего, сопротивление R_г, а коэффициент отражения записывают через табулированный полином h(р): s(р) = h(р)/v(р). Тогда (2.7) записывают как

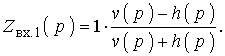                                                                         (2.8)

Например, для фильтров Чебышева третьего порядка сам полином Чебышева равен:

                                                                                     (2.9)

а полином h(р) будет:

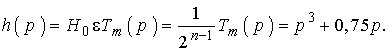                                       (2.10)

Подставляя h(р) из (2.10) и v(р) из (2.6) в (2.8), записывают Z_вх.1(р) в виде цепной дроби и по ней составляют схему двухполюсника, т. е. LC-фильтра нижних частот, нагруженного на сопротивление R_н. Элементы этой схемы представлены величинами, нормированными по частоте и по сопротивлению. Поэтому следующей операцией расчета является операция денормирования значения элементов НЧ-прототипа. После этого, используя формулы преобразования частоты, переходят от схемы НЧ-прототипа к схеме полосового фильтра. Элементы схемы ПФ, очевидно, будут иметь сразу реальные значения.

 

2.2. Синтез активных полосовых фильтров

ARC-фильтры представляют собой комбинацию пассивной RC-цепи и активного элемента. В качестве последнего чаще всего используются операционные усилители часто с двумя входами – инвертирующим и неинвертирующим. В схемах ARC-фильтров обязательно имеется обратная связь. Известно [1, 2, 3, 5, 6], что передаточная функция любой активной цепи с обратной связью записывается как

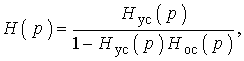
где Н_ус(р) и Н_ос(р) передаточные функции цепи прямого усиления и цепи обратной связи соответственно. Знаменатель Н(р) – это полином, например, второй степени. Корни его, т. е. полюсы Н(р) могут быть в том числе и комплексно-сопряженными. Последнее означает, что ARC-цепь эквивалентна пассивной LC-цепи, а т. к. LC-цепь обладает избирательными свойствами, то и ARC-цепь тоже может обладать избирательными свойствами, т. е. является фильтром.

Синтез ARC-фильтров, как и пассивных LC-фильтров, состоит из двух этапов: этапа аппроксимации и этапа реализации. Этап аппроксимации в обоих случаях одинаков. Этап реализации для  ARC-фильтров – отличается от LC-реализации.

Этап реализации. Вначале осуществляют переход от передаточной функции НЧ-прототипа, которая имеет вид (2.6), к передаточной функции полосового фильтра. Один из возможных вариантов такого перехода основан на использовании формулы пересчета полюсов НЧ-прототипа в полюсы ПФ:

                               (2.11)

где

 – полюсы передаточной функции НЧ-прототипа;

w₀ = 2pf₀ – находится по (2.1).

Согласно (2.11) одной паре комплексно-сопряженных полюсов нормированной передаточной функции НЧ-прототипа соответствует две пары комплексно-сопряженных полюсов денормированной передаточной функции полосового фильтра. Одному вещественному полюсу (р_нч.нор = s + j0) нормированной H(р) НЧ-прототипа (2.6) соответствует одна пара комплексно-сопряженных полюсов вида  денормированной H(р) полосового фильтра. В результате общий порядок ПФ удваивается по сравнению с порядком НЧ-прототипа.

Передаточную функцию ПФ удобно представлять произведением сомножителей второго порядка H₁(р), H₂(р), H₃(р) и т. д. Каждый из этих сомножителей реализуется в виде активного RC-звена второго порядка, а полученные звенья соединяются каскадно, образуя полную схему ПФ. Звенья ARC-фильтров в общем случае являются типовыми (одинаковыми) для фильтров, имеющих одинаковое расположение полосы пропускания на шкале частот.

 

---

назад | оглавление | вперёд