| Теория электрических цепей |
| Пример расчета полосового LC-фильтра |
назад | оглавление | вперёд |
3. Пример расчета полосового LC-фильтра
Согласно заданию на курсовую работу на входе полосового фильтра действуют периодические радиоимпульсы (рис. 1.1) с параметрами: период следования импульсов Tи = 800 мкс; длительность импульсов tи = 200 мкс; период несущей частоты Tн = 33,3 мкс; амплитуда колебаний несущей частоты Um.н = 5 В. Фильтр должен обеспечить максимально допустимое ослабление в полосе пропускания Аmax = DA = 3 дБ. Полное ослабление на границах полос непропускания Апол = 24,2 дБ. Сопротивления нагрузок фильтра слева и справа Rг =Rн = 1 кОм (рис. 2.2). Характеристика фильтра аппроксимируется полиномом Чебышева.
3.1. Расчет амплитудного спектра
радиоимпульсов
Прежде чем приступать непосредственно к расчету фильтра, необходимо определить частотный состав сигнала, поступающего на вход фильтра, т. е. рассчитать и построить график амплитудного спектра периодических радиоимпульсов, взяв за основу рис. 1.2.
Вначале находится несущая частота:
Затем рассчитывают частоты нулей огибающей спектра. Они зависят от длительности импульса:
Максимальное значение огибающей в виде напряжения, соответствующее частоте fн, находится по формуле
(3.1)
Зная максимальное значение и расположение нулей по оси частот, строим огибающую дискретного спектра периодических радиоимпульсов в виде пунктирной кривой в масштабе по оси частот (рис. 1.2).
Внутри огибающей находятся спектральные составляющие или гармоники спектра с частотами fi, где i – номер гармоники. Они располагаются симметрично относительно несущей частоты, зависят от периода следования импульсов и находятся по формуле
.
Учитывая, что
рассчитываем частоты гармоник, лежащих только справа от fн:
Частоты гармоник, лежащих слева от fн, будут:
Амплитуды напряжения i-ых гармоник находятся по формуле
(3.2)
где K = tи/Tн – количество периодов несущих колебаний косинусоидальной формы в импульсе. Например, на рис. 1.1 К = 4, а в рассматриваемом примере К = 6.
Из анализа рис. 1.2 видно, что главный «лепесток спектра» занимает диапазон частот от 25 до 35 кГц. Крайние частоты диапазона совпадают с нулями огибающей, поэтому их амплитуды равны нулю, в частности Um.4 = 0, Um.(–4) = 0.
После расчета амплитуд по (3.2) их значения отражаются в виде дискретных составляющих внутри огибающей спектра (рис. 1.2).
Полезно обратить внимание на характерную особенность спектра, связанную с понятием скважности импульсов. Если скважность q, т.е. отношение периода следования импульсов Tи к длительности импульсов tи, равна целому числу, то в спектре отсутствуют гармоники с номерами, кратными скважности. В рассматриваемом примере q = 4, поэтому в спектре будут отсутствовать (совпадать с нулями огибающей) 4, 8, 12 и т.д. гармоники слева и справа от несущей частоты.
3.2. Формирование требований к полосовому фильтру
Учитывая, что амплитуды спектральных составляющих на частотах 25 и 35 кГц равны нулю, примем за эффективную часть спектра, которую нужно выделить полосовым фильтром, диапазон частот от 26,25 кГц до 33,75 кГц. Следовательно, эти частоты будут определять частоты границы полосы пропускания фильтра fп1 иfп2 соответственно (рис. 2.1, б). Граничную частоту полосы непропускания fз2 выбираем равной частоте первой гармоники спектра сигнала, находящейся после частоты (fн + 1/tи) = 35 кГц. Этой частотой является частота f5 = 36,25 кГц. Следовательно, fз2 = = f5 = 36,25 кГц.
Используя (2.1), найдем центральную частоту ПП:
Тогда граничная частота fз.1 полосы непропускания будет
(3.3)
где
(3.4)
исходная разница амплитуд третьей и пятой гармоник в децибелах, найденная в ходе расчета спектра радиоимпульсов.
Согласно (3.2):
По (3.4) находим
а из (3.3)
Таким образом, требования к полосовому фильтру сводятся к следующему:
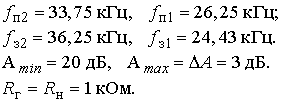
Аппроксимация передаточной функции должна быть выполнена с помощью полинома Чебышева.
3.3. Формирование передаточной функции
НЧ-прототипа
Используя (2.2), находим граничные частоты ПП и ПН НЧ-прототипа.
По формулам (2.3) получаем значения нормированных частот
Требования к НЧ-прототипу могут быть проиллюстрированы рисунком 3.1.
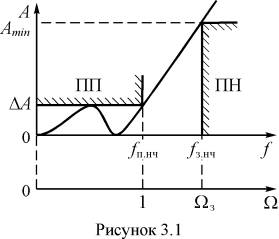
Находим коэффициент неравномерности ослабления фильтра в ПП из рассмотрения (2.5) при A = DA и W = 1, когда y(1) = Тm(1) = 1:
Порядок фильтра Чебышева находится также из рассмотрения (2.5), но при A = Aminи W =Wз, т. е. ослабление рассматривается в полосе непропускания. А в ПН полином Чебышева Тm(W) = chmarchW, поэтому
(3.5) Для вычисления функции archх рекомендуется соотношение
После подстановки в (3.5) исходных данных и вычислений получим m = 2,9. Расчетное значение m необходимо округлить в бóльшую сторону до целого числа. В данном примере принимает m = 3.
Примечание. При достаточно точных расчетах значение m во всех вариантах задания должно лежать в пределах 2 < m < 3. Если так не получилось необходимо обратиться за консультацией на кафедру.
 |
Пользуясь таблицей 3.1, находим полюсы нормированной передаточной функции НЧ-прототипа:
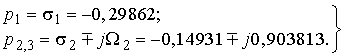(3.6)
Обратить внимание на то, что полюсы расположены в левой полуплоскости комплексной переменной р.
Формируем нормированную передаточную функцию НЧ-прототипа в виде
где v(р) – полином Гурвица, который можно записать через полюсы:
Производя вычисления, получим
(3.7)
Обратить внимание на то, что в (3.7) числитель равен свободному члену полинома знаменателя.
При расчетах необходимо придерживаться точности не менее шести значащих цифр после запятой.
3.4. Реализация LC-прототипа
Для получения схемы НЧ-прототипа воспользуемся методом Дарлингтона, когда для двусторонне нагруженного фильтра (рис. 2.2) составляется выражение для входного сопротивления Zвх.1(р) (2.8). Подставляя в (2.8) значение v(р) из (3.7) и значение h(p) из (2.10), после преобразований получим
(3.8)
Формула (3.8) описывает входное сопротивление двухполюсника (согласно схеме на рис. 2.2 фильтр, нагруженный на сопротивление Rн, это действительно двухполюсник). А если известно выражение для входного сопротивления, то можно построить схему двухполюсника, воспользовавшись, например, методом Кауэра [1¸10]. По этому методу формула для Zвх(р) разлагается в непрерывную дробь путем деления полинома числителя на полином знаменателя. При этом степень числителя должна быть больше степени знаменателя. Исходя из последнего, (3.8) преобразуется к виду
(3.9)
после чего производится ряд последовательных делений. Вначале числитель делим на знаменатель:
Затем первый делитель делим на первый остаток:
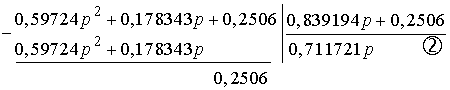
Второй делитель делим на второй остаток:
Третий делитель делим на третий остаток:
Получили четыре результата деления, которые отражают четыре нормированных по частоте и по сопротивлению элемента схемы в виде значений их проводимостей: pC, 1/pL, 1/R. Из анализа первого результата деления следует, что он отражает емкостную проводимость, поэтому все выражение (3.9) можно записать в виде цепной дроби:
(3.10)
По формуле (3.10) составляем схему (рис. 3.2), на которой С1н = 3,349; L2н = 0,712; С3н = 3,349; Rг.н = Rн.н = Rнор.
Денормируем элементы схемы НЧ-прототипа, используя соотношения:
(3.11)
где wн = wп.нч – нормирующая частота;
Rг – нормирующее сопротивление, равное внутреннему сопротивлению источника сигнала.
Используя соотношения (3.11) и значения wн иRг получаем реальные значения элементов схемы НЧ-прототипа:
3.5. Реализация пассивного полосового фильтра
Из теории фильтров известно [1¸10], что между частотами НЧ-прототипа и частотами wпф полосового фильтра существует соотношение
(3.12)
где w0 находится по (2.1).
На основании (3.12) индуктивное сопротивление НЧ-прототипа заменяется сопротивлением последовательного контура с элементами
(3.13)
а емкостное сопротивление НЧ-прототипа заменяется сопротивлением параллельного контура с элементами
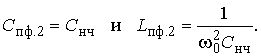(3.14)
Тогда, на основании схемы ФНЧ, изображенной на рис. 3.2 может быть построена схема полосового фильтра так, как это показано на рис. 3.3. Элементы этой схемы рассчитываются по формулам (3.13) и (3.14).
На этом расчет полосового LC-фильтра заканчивается.