| Теория электрических цепей |
| Пример расчета активного полосового фильтра |
назад | оглавление | вперёд |
4. Пример расчета активного полосового фильтра
4.1. Расчет полюсов ARC-фильтра
Требования к полосовому ARC-фильтру остаются теми же, что и к полосовому LC-фильтру. Поэтому на этапе аппроксимации синтеза ARC-фильтра можно воспользоваться результатами расчета LC-фильтра, полученными в разделах 3.1¸3.3. Причем, не самой нормированной передаточной функцией (3.7), а только ее полюсами (3.6), и, согласно (2.11), найти полюсы денормированной передаточной функции ПФ. Вначале находим:

Затем сами полюсы:
 (4.1.а)
(4.1.а)
 (4.1)(4.1.б)
(4.1)(4.1.б)
 (4.1.в)
(4.1.в)
Расчет показывает, что вместо трех полюсов нормированной передаточной функции НЧ-прототипа получается шесть полюсов передаточной функции ARC полосового фильтра, причем денормированной. Их значения удобно представить в виде таблицы 4.1.
Таблица 4.1
| Номера
|
Полюсы H(p) |
|
| |
|
|
| 1,2 |
0,7032 |
18,676 |
| 3,6 |
0,3844 |
20,9351 |
| 4,5 |
0,3188 |
16,6781 |
Следует отметить, что чередование пар полюсов в таблице 4.1 значения не имеет.
4.2. Формирование передаточной функции
Учитывая, что ARC-фильтры обычно строятся из каскадно-соединенных звеньев второго порядка, целесообразно передаточную функцию таких фильтров формировать из произведения сомножителей тоже второго порядка. Они имеют вид [1¸6]:

Тогда вся передаточная функция рассчитываемого фильтра будет:
 (4.2)
(4.2)
Коэффициенты в числителе могут иметь одинаковую величину и рассчитываться по формуле

Коэффициенты в знаменателе (4.2) находятся по формулам:
![]() (4.3)
(4.3)
где ![]() – значение полюсов
(4.1). Например,
– значение полюсов
(4.1). Например,
![]() 14064;
14064;
![]()
Значения всех рассчитанных коэффициентов сведены в таблицу 4.2.
Таблица 4.2
| Номер
|
Значения коэффициентов |
||
| ai1 |
bi1 |
bi0 |
|
| 1 2 3 |
2,9624×104 2,9624×104 2,9624×104 |
1,4064×104 0,7688×104 0,6376×104 |
3,4929×1010 4,38426×1010 2,7826×1010 |
Подставляя найденные коэффициенты в 4.2 получим:
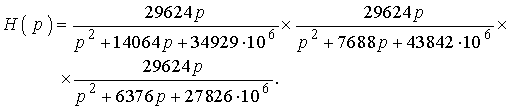 (4.4)
(4.4)
4.3. Расчет элементов схемы фильтра
В качестве типовой выбираем простейшую схему ПФ на одном операционном усилителе (ОУ) (рис. 4.1). Если составить эквивалентную схему, заменив ОУ ИНУНом, то, используя любой из методов анализа цепей [1, 5], можно получить передаточную функцию, описывающую работу схемы на рис. 4.1, в виде
 (4.5)
(4.5)
Из (4.5) видно, что рассмотренная схема является схемой второго порядка. Следовательно, для реализации функции (4.4) потребуется три подобных схемы или три звена, соединенных каскадно. Расчет элементов этих схем R1; R2; С3; С4; R5 ведется путем сравнения идентичных коэффициентов в формулах (4.4) и (4.5).
Для первого звена ПФ берутся коэффициенты из первого сомножителя (4.4):
 (4.6)
(4.6)
В системе (4.6) пять неизвестных и только три уравнения. Система нерешаема. Поэтому рекомендуется задаваться значениями, например, емкостей конденсаторов С3 и С4 (в ходе настройки фильтра при его изготовлении принято использовать переменные сопротивления, т. к. переменных конденсаторов с большой емкостью нет вообще).
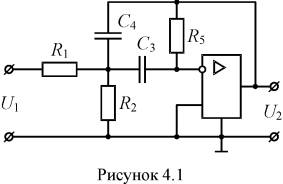
Если принять С3 = С4 = 2 нФ, то решая (4.6), получим:
R1 = 17 кОм, R5 = 71 кОм, R2 = 101 Ом.
Составляя аналогичную систему для второго звена при тех же С3 = = С4 = 2 нФ, получим:
R1 = 17 кОм, R5 = 130 кОм, R2 = 44 Ом.
Аналогично для третьего звена:
R1 = 17 кОм, R5 = 157 кОм, R2 = 58 Ом.
Рассчитанные сопротивления не соответствуют стандартным номиналам резисторов. Поэтому для сопротивлений R1 иR5 в каждом звене берутся резисторы с номиналом, ближайшим к рассчитанному значению. Сопротивление R2 берется составным, из последовательно соединенных постоянном и переменном резисторов, что позволит осуществлять общую настройку фильтра.