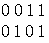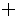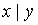2.1 Высказывания
Определение. Высказывание – повествовательное утверждение, которое либо истинно либо ложно (не то и другое одновременно).
Примеры высказываний: "Тише едешь – дальше будешь", "Париж – столица Франции". Но "Как бы чего не вышло" или "Миру – мир" не являются высказываниями.
Определение. Высказывание называется простым (элементарным), если оно рассматривается как одно неделимое целое.
Определение. Сложное высказывание – высказывание, составленное из простых с помощью логических связок.
2.2 логические связки (операции) над высказываниями.
Определение. Конъюнкцией ("и") высказываний P и Q называется высказывание, истинное тогда и только тогда, когда оба истинны. Обозначается ![]() или PQ.
или PQ.
Таблица истинности:
|
P |
Q |
P&Q |
|
л |
л |
л |
|
л |
и |
л |
|
и |
л |
л |
|
и |
и |
и |
Определение. Дизъюнкцией ("или") высказываний P и Q называется высказывание, ложное тогда и только тогда, когда оба ложны. Обозначается ![]() .
.
Таблица истинности:
|
P |
Q |
PÚ Q |
|
л |
л |
л |
|
л |
и |
и |
|
и |
л |
и |
|
и |
и |
и |
Определение. Отрицанием ("не") высказывания P называется высказывание, ложное тогда и только тогда, когда P истинно. Обозначается ![]() или
или ![]() .
.
Таблица истинности:
|
P |
Ø P |
|
л |
и |
|
и |
л |
Определение. Импликацией высказываний P и Q называется высказывание, ложное, когда P истинно, а Q ложно, и истинное во всех остальных случаях. Обозначается 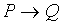 .
.
Таблица истинности:
|
P |
Q |
P® Q |
|
л |
л |
и |
|
л |
и |
и |
|
и |
л |
л |
|
и |
и |
и |
Определение. Эквивалентностью высказываний P и Q называется высказывание истинное, когда истинностные значения P и Q совпадают, и ложное в противном случае. Обозначается ![]() или
или![]() .
.
Таблица истинности:
|
P |
Q |
P~Q |
|
л |
л |
и |
|
л |
и |
л |
|
и |
л |
л |
|
и |
и |
и |
Определение. Неравнозначностью (сложение по модулю 2) высказываний P и Q называется высказывание истинное, когда истинностные значения P и Q различны, и ложное в противном случае. Обозначается ![]() .
.
Таблица истинности:
|
P |
Q |
PÅ Q |
|
л |
л |
л |
|
л |
и |
и |
|
и |
л |
и |
|
и |
и |
л |
2.3 Пропозициональные формулы
Рассмотрим алфавит ![]() , где
, где ![]() ,
, ![]() ,
,![]() .
.
Символы из ![]() называются переменными высказывания или пропозициональными переменными.
называются переменными высказывания или пропозициональными переменными.
Символы из ![]() называются логическими связками.
называются логическими связками.
Скобки из ![]() называются вспомогательными символами.
называются вспомогательными символами.
Определение. Пропозициональная формула определяется следующим образом:
1) пропозициональная переменная есть формула;
2) если P и Q – формулы, то Ø P, (P&Q), (PÚ Q) ,(P® Q) ,(PÅ Q) ,(P|Q), (P¯ Q) – формулы,
3) других формул нет.
При этом
а) внешние скобки у формул опускаются;
б) устанавливаются следующие приоритеты:
Ø – выполняется в первую очередь;
& – во вторую очередь;
Ú , ® , Å , |, ¯ – в третью очередь.
2.4 Булевы функции. Таблицы истинности.
Определение. Булевой функцией 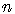 булевых переменных называется функция с областью определения
булевых переменных называется функция с областью определения 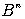 и областью значений
и областью значений ![]() , где
, где ![]() .
.
Способы задания:
1) таблицами истинности; при этом 0 интерпретируется как "ложь", а 1 – как "истина";
2) пропозициональными формулами.
Таблица истинностей некоторых логических связок:
|
x |
y |
x&y |
xÚ y |
Ø x |
x® y |
XÅ y |
x~y |
|
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
|
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
|
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
2.5 Булевы функции одной переменной
|
|
|
Обозначение |
Наименование |
|
|
|
|
Константа 0 |
|
|
|
|
Тождественная |
|
|
|
|
Отрицание |
|
|
|
|
Константа 1 |
2.6 Булевы функции двух переменных
|
|
|
Обозначение |
Наименование |
|
|
0 0 0 0 |
|
Константа 0 |
|
|
0 0 0 1 |
|
Конъюнкция |
|
|
0 0 1 0 |
|
|
|
|
0 0 1 1 |
|
|
|
|
0 1 0 0 |
|
|
|
|
0 1 0 1 |
|
|
|
|
0 1 1 0 |
|
Сложение |
|
|
0 1 1 1 |
|
Дизъюнкция |
|
|
1 0 0 0 |
|
Стрелка Пирса |
|
|
1 0 0 1 |
|
Эквиваленция |
|
|
1 0 1 0 |
||
|
|
1 0 1 1 |
|
Импликация |
|
|
1 1 0 0 |
|
|
|
|
1 1 0 1 |
|
Импликация |
|
|
1 1 1 0 |
|
Штрих Шеффера |
|
|
1 1 1 1 |
1 |
Константа 1 |
2.7 Существенные и несущественные переменные
Определение. Переменная ![]() называется существенной для булевой функции
называется существенной для булевой функции ![]() , если
, если
![]()
![]() .
.
Определение. Переменная ![]() называется несущественной для булевой функции
называется несущественной для булевой функции ![]() , если
, если ![]()
![]() .
.
2.8 Равносильные формулы. Основные равносильности
Определение. Формула называется тождественно истинной, или тавтологией, если эта формула принимает значение 1 при всех наборах значений переменных.
Определение. Формула называется тождественно ложной, или противоречием, если эта формула принимает значение 0 при всех наборах значений переменных.
2.9 Основные тавтологии
|
1. |
Закон исключенного третьего |
|
2. |
|
|
3. |
|
|
4. |
Цепное рассуждение |
|
5. |
|
|
6. |
Определение. Формулы P и Q называются равносильными (обозначается ![]() ), если при любых значениях переменных значение формулы P совпадает со значением Q.
), если при любых значениях переменных значение формулы P совпадает со значением Q.
2.10 Основные равносильности
|
1. |
Коммутативность |
|
3. 4. |
Ассоциативность |
|
5. 6. |
Дистрибутивность |
|
7. |
Идемпотентность |
|
9. |
Законы исключенного третьего и противоречия |
|
11. 12. |
Законы де Моргана |
|
13. 14. |
Законы поглощения |
|
15. |
Правило склеивания |
|
16. 18. |
|
|
20. |
Закон двойного отрицания |
|
21. 22. 23. 24. |
|
|
25. |
Коммутативность |
|
26. |
Ассоциативность |
|
27. |
Дистрибутивность |
|
28. 30. |
Замечание. Здесь P, Q и R —пропозициональные формулы.
2.11 Понятие двойственной функции
Определение. Функцией, двойственной к булевой функции ![]() , называется функция
, называется функция ![]() .
.
Определение. Функция называется самодвойственной, если ![]() .
.
Теорема. (Принцип двойственности.) Пусть ![]() ,…,
,…,![]() и
и ![]() — булевы функции и пусть
— булевы функции и пусть ![]() =
=![]() -
сложная булева функция. Тогда
-
сложная булева функция. Тогда
![]() =
=![]()
Следствие. Пусть P и Q —формулы. Если ![]() , тогда
, тогда ![]() .
.
Принцип двойственности позволяет получать из доказанных равносильностей целый ряд новых. Кроме того, СКНФ(f)=![]() .
.
2.12 Некоторые двойственные функции
|
|
|
|
|
1. |
|
|
|
2. |
|
|
|
3. |
|
|
|
4. |
|
|
|
5. |
|
|
|
Замечание. |
||
2.13 Элементарные канонические формы
Определение. Элементарной конъюнкцией называется конъюнкция переменных или их отрицаний, в которой каждая переменная встречается не более 1 раза.
Определение. Элементарной дизъюнкцией называется дизъюнкция переменных или их отрицаний, в которой каждая переменная встречается не более 1 раза.
2.14 Нормальные формы формул
Определение. Дизъюнктивной нормальной формой (Д.Н.Ф.) называется произвольная дизъюнкция элементарных конъюнкций.
Определение. Конъюнктивной нормальной формой (К.Н.Ф.) называется произвольная конъюнкция элементарных дизъюнкций.
Определение. К.Н.Ф. называется совершенной и обозначается С.К.Н.Ф., если каждая переменная входит в каждую элементарную дизъюнкцию ровно один раз с отрицанием или без.
Определение. Д.Н.Ф. называется совершенной и обозначается С.Д.Н.Ф, если каждая переменная входит в каждую элементарную конъюнкцию ровно один раз с отрицанием или без.
Пример:![]() – Д.Н.Ф;
– Д.Н.Ф; ![]() – С.Д.Н.Ф.
– С.Д.Н.Ф.
Теорема. Любая логическая функция кроме 0 имеет единственную С.Д.Н.Ф: ![]() .
.
Теорема. Любая логическая функция кроме 1 имеет единственную С.К.Н.Ф: ![]() .
.
Здесь 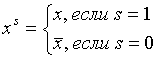 .
.
Пример. Пусть функция трех переменных задана таблицей истинности:
|
|
|
|
|
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
Записать ее С.Д.Н.Ф. и С.К.Н.Ф.
С.Д.Н.Ф.(f)=![]()
С.К.Н.Ф.(f)=![]()
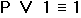
2.15 Приведение формул к нормальным формам
Любую логическую формулу (кроме 0) можно привести к С.Д.Н.Ф. следующим образом:
- Все не булевские операции заменить на булевские (&, Ú , Ø ) c помощью равносильностей:
- Все отрицания "спустить" до переменных с помощью законов де Моргана.
- Раскрыть скобки (дистрибутивность, ассоциативность).
- Удалить лишние конъюнкции, повторения переменных в конъюнкциях и константы.
- Расщепить те конъюнкции, которые содержат не все переменные.
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Для приведения к С.Д.Н.Ф:
2.16 Минимизация д.н.ф.
Д.Н.Ф, содержащую минимальное число вхождений переменных, будем считать минимальной.
Приведем 2 наиболее простых метода минимизации Д.Н.Ф. функции:
- Группировка: элементарные конъюнкции
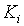 ,
, 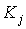 в ДНФ группируются в пары так, что после вынесения за скобку общего множителя K подформула
в ДНФ группируются в пары так, что после вынесения за скобку общего множителя K подформула 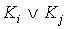 имела вид
имела вид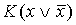 или
или 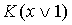 . Далее заменяем
. Далее заменяем 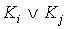 на эквивалентную ей конъюнкцию K.
на эквивалентную ей конъюнкцию K. - Метод Блейка состоит в применении двух правил:
Пример: ![]()
![]() .
.
а) обобщенное склеивание – первое правило. С помощью формулы ![]() производим операцию обобщенного склеивания в Д.Н.Ф. пока это возможно. Для этого в Д.Н.Ф. отыскиваем подформулы вида
производим операцию обобщенного склеивания в Д.Н.Ф. пока это возможно. Для этого в Д.Н.Ф. отыскиваем подформулы вида ![]() и добавляем к ним
и добавляем к ним ![]() . На этом этапе формула усложняется.
. На этом этапе формула усложняется.
б) поглощение – второе правило. Оно основано на равенстве
![]() .
.
Находим в Д.Н.Ф. конъюнкции с минимальным числом сомножителей и все конъюнкции, их содержащие, вычеркиваем.
Пример: ![]() .
.
Разумно в Д.Н.Ф. сначала применить метод группировки (как более простой), а затем метод Блейка.
2.17 Полные системы функций. Полином Жегалкина
Определение. Множество булевых функций называется полной системой, если любая булева функция может быть выражена через функции этого множества с помощью суперпозиции. Минимальная полная система называется базисом.
Примеры базисов:
![]() — дизъюнктивный базис;
— дизъюнктивный базис;
![]() — конъюнктивный базис;
— конъюнктивный базис;
![]() — базис Жегалкина;
— базис Жегалкина;
![]() — базис Пирса;
— базис Пирса;
![]() — базис Шеффера.
— базис Шеффера.
Определение Логическая функция, представленная над базисом ![]() называется многочленом Жегалкина. Он имеет вид:
называется многочленом Жегалкина. Он имеет вид:
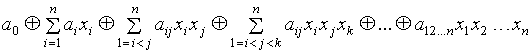 ,
,
где константы ![]() .
.
2.18 Функционально замкнутые классы функций
Ведем следующие классы Поста:
![]() =
=![]() – Класс функций, сохраняющих 0.
– Класс функций, сохраняющих 0.
![]() =
=![]() – Класс функций, сохраняющих 1.
– Класс функций, сохраняющих 1.
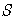 =
=![]() – Класс самодвойственных функций.
– Класс самодвойственных функций.
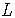 =
=![]() – Класс линейных функций.
– Класс линейных функций.
![]() =
=![]() – Класс монотонных функций.
– Класс монотонных функций.
Каждый класс Поста является функционально замкнутым, т.е. все функции, реализованные формулами над данным классом, также принадлежат данному классу.
Таблица принадлежности функциональным классам основных булевых функций:
|
|
|
|
|
|
|
|
- |
- |
|
|
- |
|
|
|
|
- |
- |
|
|
|
|
|
- |
- |
|
|
|
- |
|
- |
- |
- |
|
|
|
- |
- |
|
- |
|
|
- |
|
- |
|
- |
|
|
- |
- |
- |
- |
- |
Теорема. (Теорема Поста.) Для того, чтобы система булевых функций ![]() была полной, необходимо и достаточно, чтобы для каждого из классов
была полной, необходимо и достаточно, чтобы для каждого из классов ![]() ,
, ![]() ,
, 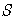 ,
, 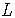 ,
, ![]() нашлась функция
нашлась функция ![]() из системы, не принадлежащая данному классу.
из системы, не принадлежащая данному классу.