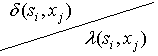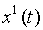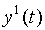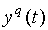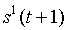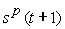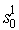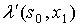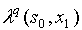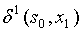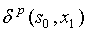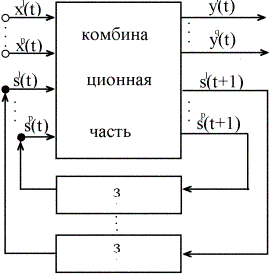
4.1 Понятие конечного детерминированного автомата Автоматы можно рассматривать как механизмы, состоящие из: блока управления, который может пребывать в различных состояниях (S внутренний алфавит); входного канала; выходного канала. Входной канал считывает входные сигналы (Х) из внешней среды. Выходной канал выдает выходные сигналы (Y) во внешнюю среду. Работа автомата протекает в дискретные такты времени t=1,2,3,…. По команде в некотором такте времени блок управления установлен в состоянии и входной канал воспринимает , тогда в этом же такте в выходной канал выдается символ , а к следующему такту +1 блок управления перейдет в состояние . Определение. К.Д.А. называется система , где - алфавит состояний, – входной алфавит, – выходной алфавит. Множества S, X, Y – конечные. – функция переходов, – функция выходов. Если в автомате выделено одно состояние , называемое начальным (обычно ), то автомат называется инициальным. 4.2 Способы задания автоматов. Таблица переходов–выходов. S\X … …           M                   M                     С помощью орграфов. Вершины граф означают состояния, а дуги – переходы между ними. Из каждой вершина исходит k дуг. Из вершины 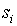проводится дуга в вершину 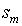в том и только в том случае, когда 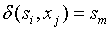для некоторого 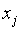. 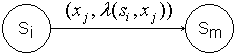Этой дуге приписывается пометка : Начальное состояние в инициальном автомате помечается символом . Описанный таким образом орграф с пометками называется диаграммой Мура. 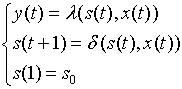С помощью канонических уравнений: в момент t=1 автомат находится в начальном состоянии 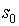. В каждый момент t=1,2,3,… дискретного времени автомат, находясь в некотором состоянии s(t) из множества S, под действием входного сигнала 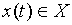выдает выходной сигнал 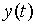из множества Y, согласно функции выходов l , а затем меняет свое состояние на s(t+1) согласно функции переходов d. Для определения множества состояний автомата необходимо уяснить содержательный смысл и назначение понятия состояния. После преобразования входного сигнала в выходной его значение к следующему такту времени теряется. Иначе говоря, в любой тактовый момент t в устройстве нет информации о сигналах в предыдущие моменты, то есть о значениях ,, ,… . Поэтому, если при вычислении значения функции переходов и выходов по формуле необходима информация об этих тактовых моментах, то ее нужно каким-либо образом "запомнить". В этом и состоит содержательное назначение состояний. Состояния – это вспомогательные объекты, которые подбираются таким образом, чтобы в совокупности с входным значением однозначно определить выходное значение . Обычно состояния кодируют ту информацию, которая поступила до момента t. Пример. 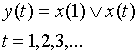Построить таблицу переходов–выходов К.Д.А, реализующего функцию: Чтобы на любом, отличном от первого, такте иметь информацию о , введем два следующих состояния: ={"на первом такте поступил 0"}; ={"на первом такте поступила 1"}. И –начальное состояние. 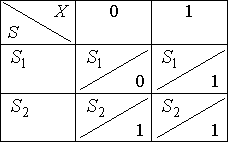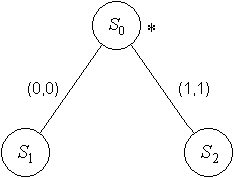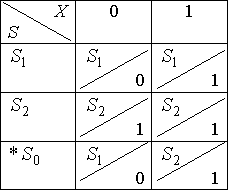Построим таблицу переходов–выходов: Для нарисуем диаграмму Мура: И дополним таблицу переходов–выходов: 4.3 Эквивалентные состояния. Минимизация к.д.а. Определение. Две диаграммы Мура называются изоморфными, если они могут быть превращены одна в другую переобозначением вершин. Определение. Два автомата называются изоморфными, если их диаграммы Мура изоморфны. Рассмотрим два автомата и с одинаковыми входным и выходным алфавитами. Определение. Состояния и называются неотличимыми (эквивалентными) тогда и только тогда, когда для любого входного слова х результат работы автомата такой же, как и для . В частном случае, когда =, то речь идет о неотличимых состояниях одного автомата. Определение. Автоматы и называются неотличимыми (эквивалентными) тогда и только тогда, когда для любого состояния найдется эквивалентное ему состояние и обратно. Неотличимые автоматы осуществляют одно и то же отображение входных слов в выходные. Определение. Автомат А называется приведенным, если в нем нет эквивалентных (неразличимых) состояний. Число состояний в приведенном автомате минимально. Для любого автомата существует эквивалентный ему приведенный автомат А. Процедура нахождения такого автомата называется минимизацией автомата . 4.4 Алгоритм минимизации конечного автомата. Шаг 1: два состояния s и t относим в один класс , если для любого входного символа x значение функции выхода s совпадает со значениями функции выхода t. В результате получим r классов: . M Шаг k: два состояния s и t из одного класса , полученного на предыдущем шаге, относим в один класс , если для любого значения входного символа значения функций состояний принадлежат одному и тому же классу из предыдущего шага. Если шаг k не изменяет разбиения, то процесс останавливается. Доопределяем функции перехода и выхода и строим таблицу переходов –выходов. Пример. 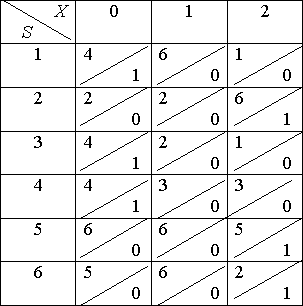Минимизировать автомат, заданный таблицей: Шаг 1: Первое, третье и четвертое состояния отнесем в один класс состояний, а второе, пятое и шестое – в другой: ; Шаг 2: Выпишем значения функции переходов для состояний из класса : ; ; ; ; ; ; Видно, что 1 и 3-е состояния относим в один класс этого шага , а четвертое состояние – в другой . Проанализировав аналогичным образом значения функции выходов для состояний из класса , видим: ; ; ; ; ; ; , т.е. все они остаются в одном классе. В результате получим разбиение на классы: ; ; Шаг 3: ; ; . Дальнейшего разбиения классов не происходит, поэтому процесс останавливается. Класс назовем состоянием , класс состояний назовем состоянием , а класс – состоянием . 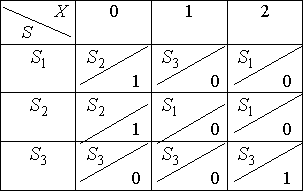Построим таблицу переходов–выходов: Построенный автомат – минимальный. 4.5 Каноническая таблица. Канонические уравнения. Реализация К.Д.А. осуществляется на основе канонических уравнений, которые находятся с помощью канонической таблицы. Каноническая таблица строится следующим образом по таблице переходов–выходов или диаграмме Мура. Аргументы функций l и d находятся в столбцах слева, а справа – их значения. 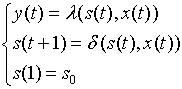S\X … …                     M                   M                     s(t) x(t) y(t) s(t+1) … … … … … … … … … … … … … … … … Канонические уравнения имеют вид: Элементы множеств S, X, Y кодируют двоичными наборами, соблюдая при этом следующие условия: разным элементам в каждом из множеств S, X, Y соответствуют разные кодовые наборы; длины кодовых наборов в каждом из множеств S, X, Y должны совпадать и быть по возможности минимальными; начальному состоянию соответствует набор . После кодирования , , принимают вид: = = = Таблица преобразовывается к скалярному виду следующим образом: … … … …         … . …   …   … …   … * Для того, чтобы представить , как булевы функции, необходимо, чтобы они были всюду определены. С этой целью к таблице добавляются строки, содержащие в левой части недостающие наборы, а в правой части – прочерки. Затем, прочерки заполняются 0 и 1 (функции доопределяются) так, чтобы по соответствующим столбцам значений l и d можно было записать формулу в виде СКНФ или СДНФ или в каком-нибудь другом наиболее простом виде. Пример. 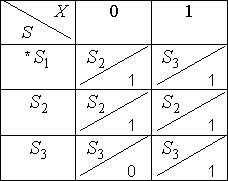Автомат задан таблицей переходов – выходов: Записать его канонические уравнения. Закодируем состояние 00 (начальное), состояние 01, состояние 10. Запишем каноническую таблицу: s(t) x(t) y(t) s(t+1) 00 0 1 01 00 1 1 10 01 0 1 01 01 1 1 01 10 0 0 10 10 1 1 10 И преобразуем ее к скалярному виду: (t) (t) x(t) y(t) (t+1) (t+1) 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 0 1 0 1 1 1 0 1 1 0 0 0 1 0 1 0 1 1 1 0                         Две последние строки доопределим следующим образом: (t) (t) x(t) y(t) (t+1) (t+1) 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 0 1 0 1 1 1 0 1 1 0 0 0 1 0 1 0 1 1 1 0 1 1 0 1 0 0 1 1 1 1 0 0 Запишем канонические уравнения: 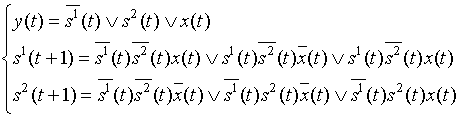. Осталось упростить уравнения. 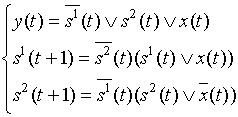Применим метод группировки =; =; и запишем канонические уравнения в более простом виде: 4.6 Функциональные и логические элементы. Проектирование дискретных устройств. Под функциональным элементом понимают устройство, реализующее элементарную функцию. Функциональные элементы, соответствующие булевым функциям, называют логическими элементами. Канал – это линия, по которой передается информация. Узел – точка, в которую передается или из которой считывается информация. На схемах канал обозначается прямой линией, а узел – кружочком. Точки ветвления каналов обозначаются жирной точкой, чтобы отличать их от точек пересечения линий на схеме. 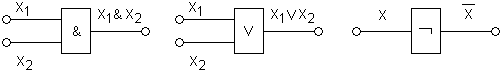Построение схемы, реализующей булеву функцию. 1 ЭТАП: Функции l и d реализуются как булевы функции, зависящие от булевых переменных s(t) и x(t). Шаг 1. Поиск в формуле подформул, которые могут быть реализованы некоторыми функциональными элементами. Изображение их на схема. Шаг 2. Поиск подформул, аргументами которых могут являться функции, реализованные функциональными элементами на предыдущем шаге. Для найденных подформул реализующие их функциональные элементы изображаются на схеме. Совмещаются соответствующие входные и выходные узлы элементов. Шаг 3. Шаг 2 повторяется до тех пор, пока не будут исчерпаны все формулы. Пример. 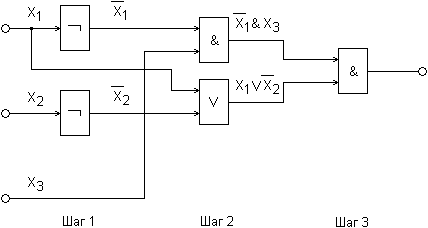Построить схему для вычисления функции 2 ЭТАП: Для сохранения значений состояний s(t+1) до следующего такта в схему вводится необходимое количество элементов памяти. Элемент, обеспечивающий запоминание одного бита двоичной информации в течение 2 такта, называется задержкой (триггером). На схеме такой элемент обозначается квадратом с буквой "з". Память содержит необходимое количество таких элементов.

назад | содержание