6.2 Пролетный режим работы ЛПД
Принцип работы ЛПД с n+-р-i-р+-структурой. Этот режим работы диода основан на использовании лавинного пробоя и пролетного эффекта носителей в обедненной области различных полупроводниковых структур. Распределение поля в этой области, определяющее физические процессы в диоде, зависит от структуры и закона распределения концентрации примесей в областях структуры. Ниже будет рассмотрена n+-р-i-р+-структурой (диод Рида), так как физические процессы в этом диоде наиболее четко разделены (рис. 6.4, а).
Распределение концентрации примесей в областях структуры показано на рис. 6.4, б. Концентрация примеси в крайних областях р+ и n+ много больше, чем в р-области; по концентрации носителей i-область близка к собственному полупроводнику. Напряженность Е – линейно уменьшается в p-области и остается постоянной в i-области (рис. 6.4, в).
Вследствие сильной зависимости от напряженности поля коэффициенты ионизации an и aр будут изменяться по направлению х более резко, чем Е (рис. 6.4 г). Зависимость а(х) располагается в пределах р-области. Для упрощения принято an=aр=a. Условие лавинного пробоя (6.11) означает равенство единице площади кривой а(х). Слой умножения, где возможно лавинное умножение носителей, очень узкий и находится в основном справа от сечения х=0, в котором напряженность поля максимальна. Левая граница слоя приблизительно совпадает с сечением x=0. За правую границу условно примем координату xл так, чтобы на участке 0 – xл практически закончилось лавинное умножение. Часть структуры от xл до границы р+-области называют слоем дрейфа. В этой части прибора нет лавинного умножения, но напряженность поля еще достаточно велика, чтобы дрейфовая скорость носителей была равна скорости насыщения vн (см. рис. 6.1)
В условиях генерации или усиления колебаний на ЛПД кроме постоянного напряжения имеется синусоидальное. Поэтому к напряженности поля Е в статическом режиме, показанной на рис. 6.4, в добавляется синусоидально изменяющаяся во времени напряженность ноля Е(t). Если пренебречь влиянием объема заряда, то напряженность переменного поля будет одинаковой во всех точках слоев умножения и дрейфа. В этом случае в данный момент времени отклонение от статического значения поля не будет зависеть в этих слоях от координаты х. На рис. 6.5 сплошная линия 1 показывает распределение напряженности поля в статическом режиме (или когда переменное поле проходит через нулевое значение), а пунктирные линии соответствуют максимальным 2 и минимальным 3 значениям результирующей напряженности поля, наступающим при амплитудных значениях синусоидальной напряженности поля E(t).
Возможность усиления в ЛПД объясним с помощью пространственно-временной диаграммы (рис. 6.6).
Напряженность синусоидального во времени поля E(t) существует во всем пространстве от х=0 до x=ω, но на рисунке она изображена при х=xл, соответствующем началу слоя дрейфа. Позже будет объяснено, что при большой амплитуде напряженности поля лавинный процесс приводит к образованию короткого сгустка носителей, запаздывающего на четверть периода от максимума поля. Этому сгустку соответствует короткий импульс лавинного тока iл(t) на границе х=xл между слоями умножения и дрейфа. Далее носители сгустка двигаются в электрическом поле слоя дрейфа, пока на достигнут его гратгцы x=ω при угле пролета θдр. Пространственно-временная диаграмма для слоя дрейфа изображена на 7.6 прямыми литиями, так как дрейфовая скорость носителей постоянна.
Угол пролета при выбранной ширине слоя ω зависит от частоты. Если θдр<π, ςо носители все время пролета находятся в тормозящем полупериоде поля и отдают свою энергию полю, вызывая его увеличение. При θдр>π οоследнюю часть пути в области дрейфа носители летят в ускоряющем полупериоде поля, что ослабляет эффект предыдущего взаимодействия и приводит в целом к снижению энергии, передаваемой носителями полю за все время пролета. Если θдр=2π, ςо эффект взаимодействия носителей и поля исчезает.
На рис. 6.6 при х=ω показана зависимость дрейфового тока от времени iдр(t) в виде узкого импульса, повторяющего импульс iл(t). Изображена также кривая наведенного тока iнав(t), созданного движением короткого сгустка на пути от х=xл до x=ω. В случае короткого сгустка форма кривой наведенного iнав(t) созданного движением короткого сгустка на пути от х=xл тока близка к прямоугольной. Разложением в ряд Фурье может быть определена первая гармоника iнав(1) этого тока. В идеальном случае она находится в противофазе с полем, если θдр=π. Οо амплитуде первой гармоники наведенного тока и амплитуде поля можно найти мощность, передаваемую потоком носителей электрическому нолю.
Ток проводимости в слое умножения. Систему уравнений непрерывности для слоя умножения можно записать в виде
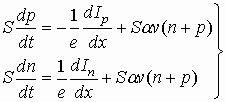(6.12)
где v—скорость электронов и дырок (для упрощения приняты равными); S—площадь сечения структуры.
Левая часть каждого уравнения есть изменение числа носители в слое длиной 1 см и сечением S за 1с. Первые слагаемые в правой части учитывают изменение числа носителей за 1 с вследствие прохождения тока. Вторые слагаемые показывают, сколько пар носителей в рассматриваемом объеме образуется за 1 с электронами (Sαvn) и дырками (Sαvp). В (6.12) не учтена рекомбинация носителей в слое умножения, так как обычно время пролета носителей в этом слое много меньше времени жизни.
В слое умножения ток вызван дрейфовым движением носителей. При пренебрежении диффузией носителей дырочная и электронная составляющие тока
Ip = Sеvр, In = Sеvn, (6.13)
а весь ток
I = Ip+In = Sеv(n+p). (6.14)
При большой напряженности поля, характерной для лавинного пробоя, скорость носителей равна так называемой скорое, насыщения—максимально возможной скорости носителей в полупроводниках (vн = 107 см/с). Поэтому время пролета носителей слоя лавинного умножения
(6.15)
Из (6.13) следует, что
Подставляя эти величины в (6.12) и учитывая (6.14), получим
Складывая эти уравнения, получим
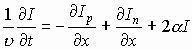(6.16)
Для решения (6.16) принимается допущение, что полный ток I равный сумме Ip и In, не зависит от координаты х, как в статическом режиме. Тогда I(х) = const. а вместо частной производной dI /dt можно записать dI/dt.
Умножим (6.16) на dx и проинтегрируем по координате x от 0 до xл:
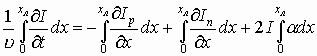
Это уравнение с учетом (6.15) приводится к виду
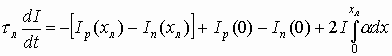(6.17)
Вычислим разности токов, входящие в правую часть (6.17), Полный ток в сечении х=xл I=Ip(xл)+In(xл), поэтому
(6.18)
Полный ток в сечении х=0 I=Ip(0)+In(0). Подставляя эту разность в (6.17), получим
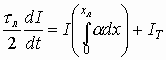(6.19)
где
Iт=Ip(0)+In(xл) (6.20)
Очевидно, что Ip(0)=Iр0, где Iр0 — ток, создаваемый дырками, приходящими в слой умножения слева из n-области, а In(0)=In0, где In0 — ток, создаваемый электронами, входящими в слой умножения справа. Таким образом, (6.20) определяет тепловой ток перехода Iт, (или ток насыщения), которым при большом коэффициенте лавинного умножения можно пренебречь.
Токи в слое умножения при малой амплитуде поля. Обычно вводят среднее значение коэффициента ионизации по слою умножения
(6.21)
Тогда вместо (6.19) можно написать
(6.22)
Пренебрегая в последнем уравнении Iт получаем
(6.23)
Используем (6.23) для определения переменного тока, появляющегося при приложении к диоду переменного напряжения. Рассмотрим режим, когда амплитуда переменной составляющей напряженности поля Ел в слое умножения много меньше постоянной составляющей (режим малых амплитуд). Постоянную составляющую примем равной критическому, значению Екр, удовлетворяющему условию лавинного пробоя (6.11). Тогда мгновенное значение напряженности поля
, 
(6.24)
Максимальные и минимальные значения Е в структуре показаны на рис. 6.5
Будем также предполагать в режиме малых амплитуд изменения коэффициента ионизации α и тока I малыми, т. е.
, 
(6.25)
, 
(6.26)
где — комплексные амплитуды соответствующих величин. В первом приближении можно записать
(6.27)
Используя (6.25) и (6.27), получаем
(6.28)
Определим величину 
, входящую в(6.23). На основании (6.28)
По условию пробоя (6.11) и (6.21) 
= 1 поэтому
(6.29)
Подставляя (6.26) и (6.29) в (6.23) и пренебрегая членами второго порядка малости, получаем
(6.30)
Если ширина слоя умножения xл сравнительно небольшая, то мал и переменный заряд в этом слое. Поэтому напряженность переменного поля практически одинаковая по всему слою, так что падение напряженности на слое умножения
Uл=Eлxл (6.31)
Используя (6.30) и (6.31), получаем
Iл=Uл/iωLл (6.32)
где
Lл=τл/2I0α’ (6.33)
эквивалентна индуктивности, так как ток отстает от напряжения на 90°, и названа индуктивностью лавины.
Полученный результат является следствием инерционности процесса образования лавины носителей. Когда поле пройдет максимальное значение и начнет уменьшаться, концентрация носителей еще продолжает возрастать. Максимумы концентрации носителей и тока в линейной теории достигаются к моменту времени, когда переменная составляющая поля, уменьшаясь, проходит через нулевое значение (отставание по фазе на 90°, рис. 6.7).
С увеличением переменного напряжения на слое умножена Uл (рис. 6.7, а) предположение о малости сигнала перестанет вы подняться. Изменение тока во времени будет все сильнее отличаться от синусоидального закона (6.26) и начнет приобретав импульсный характер. Как показывает специальное решение (6.23), положение максимума импульса тока (пунктир на рис. 6.7, б) практически совпадает с максимальным значением тока при слабом сигнале. Поэтому слой умножения приближенно можно рассматривать как источник импульсов тока, запаздывающих по отношению к максимальному значению напряжения на четверть периода.
Ток смещения в слое умножения с учетом (6.24) и (6.31)
(6.34)
где
(6.35)
эквивалентная емкость слоя умножения, а S — площадь сечения.
Полный ток слоя равен сумме тока проводимости (6.32) и тока смещения (6.34), но последний при пренебрежении влиянием переменного заряда совпадает с емкостным током. Поэтому
(6.36)
Соответственно полная проводимость слоя умножения
(6.37)
Эквивалентная схема слоя умножения при малой амплитуде поля. В соответствии с (6.37) слой умножения может быть представлен эквивалентной схемой — параллельным колебательным контуром, содержащим индуктивность Lл ,и емкость Сл (рис. 6.8). Полное сопротивление слоя из (6.37)
(6.38)
где
(6.39)
— собственная резонансная частота контура, называемая лавинной частотой. С учетом (6.15), (6.33) и (6.35)
(6.40)
где i0=I0/S — плотность тока, а vн—скорость насыщения.
Лавинная частота fл пропорциональна корню 'квадратному из плотности тока и производной от коэффициента ионизации по напряженности поля α'.
Токи в слое дрейфа при малой амплитуде поля. Рассмотрим теперь составляющие полного тока слоя дрейфа и его полное сопротивление. В этом слое постоянная составляющая напряженности поля меньше критического значения Екр, но достаточно велика, чтобы скорость носителей оставалась практически равной скорости насыщения vн. При постоянстве скорости ток проводимости в любом сечении х в момент временя t равен тому току, который был в начале слоя дрейфа в более ранний момент временя t – τx, где τx — время пролета от начала слоя до данного сечения. Для удобства рассмотрения поместим начало координат на границе слоев умножения и дрейфа, тогда τx=x/vн. Теперь в области дрейфа ток проводимости
Iдр (x,t)= I0 (0,t – τx) (6.41)
где I0(0,t – τx) – ток проводимости в начале слоя дрейфа (x=0),
в момент времени t – τx можно определить по (6.26). Переменная составляющая тока проводимости
(6.42)
Определим наведенный ток, создаваемый переменным зарядом в слое дрейфа в момент времени t.
(6.43)
где
(6.44)
— время пролета в слое дрейфа.
Комплексная амплитуда наведенного тока в (6.43)
(6.45)
Емкостный ток слоя дрейфа
(6.46)
где емкость слоя дрейфа
(6.47)
С учетом (6.45) и (6.46) полный ток
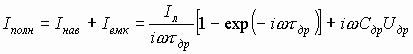(6.48)
Из (6.36) можно найти связь Iл с полным током
(6.49)
Следовательно, из (6.48) можно записать полное сопротивление слоя дрейфа
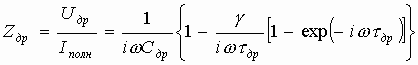(6.50)
Эквивалентная схема слоя дрейфа при малой амплитуде поля. После преобразований (6.50) сводится к виду
(6.51)
где активное сопротивление дрейфового слоя
(6.52)
реактивное сопротивление дрейфового слоя
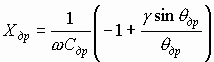(6.53)
В (6.52) и (6.53) использовано обозначение для угла пролета
(6.54)
Эквивалентная схема слоя дрейфа показана на рис. 6.8.
Рис. 6.9 Рис. 6.10
Из (6.52) следует, что активное сопротивление слоя отрицательно на всех частотах ω>ωл (γ<0), κроме частот, на которых Rдр=0 (при θдр=2πn, n=1, 2,....). Зависимость Rдр от угла пролета θдр показана на рис. 6.9. Максимум отрицательного сопротивления наблюдается вблизи θдр=π. При дальнейшем увеличении θдр до 2π, Rдр уменьшается до нуля.
Таким образом, диапазон частот, в котором может быть обеспечено отрицательное сопротивление, велик. Однако, обычно считают, что ЛПД хорошо работает лишь на частотах, соответствующих углу пролета θдр=ωτдр=π. Θз этого условия с учетом (7.44) для узкого слоя умножения (xл<<ω) можно определять пролетную частоту
fпр = ωпр/2π = 1/2τдр = vн/2ω. (6.55)
Если ω = 5 мкм и vн ≈107 м/с, то fпр=20 ГГц.
Эквивалентная схема ЛПД в пролетном режиме работы для малого сигнала показана на рис. 6.8. Контур LлСл характеризует процессы в слое умножения, а Rдр и Хдр — процессы в слое дрейфа. Полное сопротивление ЛПД Z=R+iX. Примерная зависимость активного R и реактивного Х сопротивлений от частоты показана на рис. 6.10. На частотах ниже лавинной fл активное сопротивление ЛПД положительное, а реактивное имеет индуктивный характер. На частотах выше fл активное сопротивление отрицательное, а реактивное становится емкостным. Наличие отрицательного сопротивления и позволяет использовать ЛПД для создания генераторов и усилителей СВЧ.
назад | оглавление | вперёд