Глава 6. Лавинно-пролетные диоды (ЛПД)
6.1 Лавинное умножение носителей заряда
Зависимость дрейфовой скорости от поля. Для последующего рассмотрения полупроводниковых приборов необходимо знать зависимость направленной скорости носителей (дрейфовой скорости) от напряженности электрического поля для кремния и германия. Эта зависимость vдр(Е) показана на рис. 6.1.
Дрёйфовая скорость связана с напряженностью поля Е соотношением
vдр(Е) = µЕ (6.1)
где µ — подвижность носителей, пропорциональная среднему времени пробега, носителей между двумя последовательными соударениями с атомами кристаллической решетки.
Чем больше время пробега τ, тем большую скорость направленного движения приобретет носитель в том же электрическом поле. В слабых электрических полях скорость направленного движения много меньше тепловой скорости, поэтому среднее время пробега определяется тепловой скоростью и от напряженности поля практически не зависит. В этом приближении подвижность носителей также не зависит Е, т.е. в (6.1) дрейфовая скорость пропорциональна Е (начальный участок на рис. 6.1). Напряженность Е определяет прибавку энергии носителя к тепловой энергии при термодинамическом равновесии, когда поле отсутствует. Поэтому линейный начальный участок означает также, что дрейфовая скорость пропорциональна разности полной энергии при наличии поля и тепловой энергии носителей при его отсутствии.
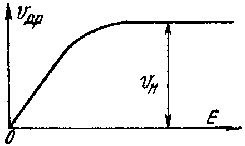
Рис. 6.1
Когда с ростом Е скорость vдр станет сравнимой с тепловой скоростью, время пробега заметно уменьшается, так как длина побега определяется кристаллической решеткой и остается неизменной. Это означает уменьшение подвижности носителей и нарушение в (6.1) пропорциональности между скоростью и напряженностью поля. При больших полях на кривой vдр(Е) появляется участок насыщения. Для объяснения насыщения скорости предполагают, что в сильном поле независимо от его величины носитель заряда при любом соударении с кристаллической решеткой теряет одну и ту же энергию ∆Е. Тогда за 1 с, в течение которой происходит 1/τ соударений, потеря энергии составит ∆Е/τ. Так как рассматривается стационарное состояние, то эта потеря энергии должна восполняться за счет работы силы электрического поля Fэл = еЕ на пути, который за 1 с численно равен дрейфовой скорости, т. е.
∆Е/τ = еЕvдр. (6.2)
кроме этого должен выполняться закон сохранения импульса (количества движения)
Fэл τ = m vдр (6.3)
Из (7.2) и (7.3) следует, что
Таким образом, если в сильном поле ∆Е от поля не зависит, то дрейфовая скорость также не зависит от него. Это предельное значение дрейфовой скорости называют скоростью насыщения vн. Значение vн зависит от полупроводникового материала и типа носителя (электрон, дырка) и составляет примерно 107 см/с.
Ударная ионизация. Если энергия движущихся в электрическом поле носителей заряда превысит некоторое определенное значение, начнется ударная ионизация: соударение носителя с нейтральным атомом кристаллической структуры приводит к образованию пары новых носителей — электрона и дырки.
Для количественной характеристики этого процесса вводят коэффициенты ионизации an и aр для электронов и дырок — число электронно-дырочных пар, создаваемых на единице пути (1 см) электроном и дыркой соответственно. Коэффициенты an и aр сильно зависят от напряженности поля. Ударная ионизация наблюдается при большой напряженности электрического поля (Е>105 В/см). Зависимость an и aр от напряженности поля для германия, кремния и арсенида галлия показана на рис. 6.2. Увеличение напряженности поля в 2—3 раза может привести к росту коэффициентов ионизации на четыре-пять порядков. В рассматриваемой области значений напряженности поля зависимость an и aр от Е может быть представлена степенной функцией с показателем, лежащим в пределах от 3 до 9 в зависимости от материала и типа носителей. Для арсенида галлия коэффициенты примерно одинаковы (an ≈ aр). У кремния и германия an ≠ aр В дальнейшем для упрощения рассмотрения будем принимать их равными (an =aр =a).
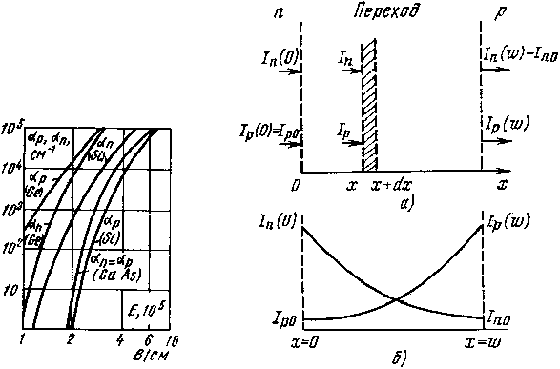
Рис. 6.2 Рис. 6.3
Лавинное умножение носителей в p-n-переходе. В полупроводниковых диодах ударная ионизация может происходить в области p-n-перехода, если в ней создана достаточно большая напряженность поля. С этим явлением связан резкий рост обратного тока перехода, называемый лавинным пробоем.
Ток через переход при обратном напряжении вызван движением неосновных носителей. Дырки, экстрагированные из n-области, двигаются в переходе по направлению к р-области, а электроны, экстрагированные из р-области, перемещаются через переход в n-область. Пусть начальный дырочный ток на левой границе перехода (х = 0) Ip0, а начальный электронный ток на правой границе (x = ω) In0 (рис. 6.3, a). Вследствие ударной ионизации число двигающихся дырок растет слева направо, а электронов — в противоположном направлении. Соответственно в этих направлениях возрастают дырочная и электронные составляющие тока.
Пусть Ip и In дырочный и электронный токи в произвольном сечении х. В слой dx в этом сечении за 1 с слева входит Ip/е дырок, а справа In/е электронов (е —заряд электрона). Каждый носитель, проходя слой dx, создает adx пар носителей (электрон—дырка), если считать коэффициенты ионизации электронов и дырок равными. Поэтому прирост числа дырок на длине dx
d Ip/е = (Ip/е) α dx + (In/e) α dx = (I/e) α dx. (6.4)
где
I =Ip +In (6.5)
— суммарный (полный) ток в переходе, не зависящий от координаты. Тогда из (6.4) приращение дырочного тока в слое
dIp=α Idx. (6.6)
Аналогично прирост электронного тока с уменьшением координаты х
dIn = – α Idx. (6.7)
Рассмотрим несимметричный p-n-переход, в котором концентрация акцепторов много меньше концентрации доноров. Концентрация неосновных носителей обратно пропорциональна концентрации примеси, поэтому начальный дырочный ток будет много больше начального электронного тока (Ip0>>In0). В этом случае можно считать, что лавинное умножение вызвано дырками, приходящими из n-области. Интегрируя (6.6) в пределах от х=0 До x=ω θ используя граничные значения токов Ip0 и Ip(ω) получим
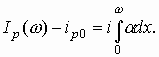(6.8)
Полный ток I вынесен за знак интеграла, так как он не зависит от координаты. Вследствие лавинного умножения Ip(ω) > Ip0.
В рассматриваемом случае Ip0 >> In0, поэтому Ip(ω) >> In0 и найденный в сечении x=ω οолный ток
I = Ip(ω) + In0 ≈ Ip(ω)
Подставляя в (6.8) I вместо Ip
(ω), получим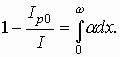
или
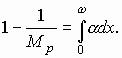(6.9)
где
Mp= I /Ip (6.10)
—коэффициент лавинного умножения, если процесс умножения в переходе начинается дырками.
Аналогично можно ввести Mn = I / In, если процесс умножения начинают электроны (случай In0 >> Ip0).
Лавинный пробой. Принято считать, что лавинный пробой наступает при таком обратном напряжении на переходе, когда коэффициент лавинного умножения обращается в бесконечность. Если начало лавинного умножения вызвано дырками (Ip0 >> In0), то условие лавинного пробоя можно найти из (6.9), считая, Мр→ ∞. Это возможно при
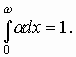(6.11)
Условие (6.11) имеет простой физический смысл: для возникновения лавинного пробоя необходимо, чтобы каждый электрон и каждая дырка, вошедшие в переход и возникающие в переходе создавали в среднем по одной электронно-дырочной паре. Если aр ≠ an, то носители, имеющие больший коэффициент ионизации должны создавать при прохождении перехода в среднем более одной пары, чтобы скомпенсировать уменьшение коэффициента ионизации носителей другого типа.
Коэффициент α зависит от напряженности поля, распределение которого в переходе можно найти из решения уравнения Пуассона, считая напряженность поля на границах перехода нулевой. Тогда в (6.11) неизвестным будет только ширина перехода ω. Следовательно, можно определить ширину перехода, при которой наступит лавинный пробой, а затем по известному pacпределению напряженности пробоя вычислить напряжение пробоя.
назад | оглавление | вперёд