8.2 Квантовые переходы. Спонтанные переходы – самопроизвольные квантовые переходы из верхнего энергетического состояния в нижнее. Уровень, соответствующий наименьшей возможной энергии, называется основным, а остальные – возбуждёнными. Частота излучения определяется из постулата Бора , где энергия верхнего (εj ) и нижнего (εi ) уровней; h- постоянная Планка. Частота называется частотой квантового перехода. Число частиц с одинаковой энергией в единице объёма называется населённостью уровня. Пусть номер верхнего уровня j=2, а нижнего i=1. Обозначим населённости этих уровней N2 и N1. При спонтанных переходах происходят изменение населённости уровней, уменьшение верхнего 2 и увеличение нижнего 1. 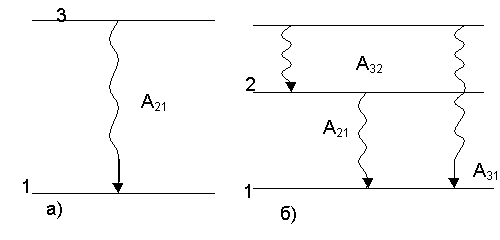Рис. 8.2 Уменьшение населённости уровня 2 в результате только спонтанных переходов за время dt пропорционально населённости этого уровня N2 и времени dt: dN2= -A21N2dt, где A21_- коэффициент Эйнштейна для спонтанных переходов, определяющий вероятность спонтанного перехода в 1 с. Решив, получить экспоненциальный закон уменьшения населённости уровня 2 во времени: N2(t)=N2(0)exp(­A21t), где N2(0) – населённость в момент времени t = 0. Насколько уменьшится населённость N2 настолько же возрастёт населённость N1 так как общее число частиц в объёме остаётся неизменным. Из этого следует, что через время t=1/A21 населённость N2 уменьшится в е = 2,718 раза по сравнению с начальным значением N2(0). Величина τ²=1/A21 характеризует время жизни в возбуждённом состоянии 2 и называется временем жизни на уровне. Коэффициент Эйнштейна объёма в 1с, или среднее число частиц, совершивших самопроизвольный переход из верхнего состояния в нижнее, т. е. имеет размерность и может быть любым, в отличии от математической вероятности, меняющейся от 0 до 1. За 1 с в единице объёма число спонтанных переходов N21(c)=A21N2. При каждом спонтанном переходе частицы выделяется квант энергии, поэтому за 1 с с учётом излучается энергия P21(c)=n21(c)hν21=A21N2hν21. Случайность спонтанных переходов означает, что различные частицы излучают неодновременно и независимо, т. е., фазы электромагнитных волн, излучаемых отдельными частицами, не согласованы друг с другом. Излучение обычных источников света есть результат спонтанных переходов. В системе частиц, имеющих несколько энергетических уровней возможны спонтанные переходы частиц с данного уровня на нижние. Полная вероятность Ај спонтанного перехода с уровня ј на все нижние уровни ί πавна сумме вероятностей отдельных переходов А јί: A ј= Σ A јі = A ј1+Aј2+...+A ј(ј-1). Уровни, для которых вероятность спонтанных переходов очень мала, называют метастабильными. Время жизни на уровне j в многоуровневой системе определяется аналогично с учётом. τ j=1/A j. Вынужденные переходы – это квантовые переходы частиц под действием внешнего электромагнитного поля, частота которого совпадает или близка к частоте перехода. При этом возможны переходы с верхнего уровня 2 на нижний 1 и с нижнего на верхний. В первом случае под действием внешнего электромагнитного поля с частотой ν21 происходит вынужденное испускание кванта энергии hν21. Особенность вынужденного испускания состоит в том, что появившийся фотон полностью идентичен фотону внешнего поля. Вынужденное излучение имеет такие же частоту, фазу, направление распространения и поляризацию, как и вынуждающее излучение. Поэтому вынужденное излучение увеличивает энергию электромагнитного поля с частотой перехода ν21. Это служит предпосылкой для создания квантовых усилителей и генераторов. В противоположность этому для перевода частицы из нижнего энергетического состояния 1 в верхнее 2 необходимо затратить энергию внешнего поля, равную разности энергии верхнего и нижнего уровней. Таким образом, при каждом вынужденном переходе снизу вверх затрачивается квант энергии внешнего поля hν21. Вынужденные переходы, так же как и спонтанные, имеют статистический характер. Поэтому вводится вероятностные коэффициенты: W21 - вероятность вынужденного перехода сверху вниз и W12 - снизу вверх в 1с. Эти вероятности определяются соотношениями, W21=B21uν, W12=B12uν, где В21 и В12 - коэффициенты Эйнштейна для вынужденных переходов с излучением и поглощением энергии соответственно. Число вынужденных переходов сверху вниз с излучением энергии в единицу времени в единицу объёма пропорционально вероятности W21 и населённости верхнего уровня N2. n21(в)=W21N2=B21uνN2. Аналогично при тех же условиях число вынужденных переходов снизу вверх с поглощением энергии: n12(в)=W12N1=B12uνN1 Соотношение между коэффициентами Эйнштейна. Связь между коэффициентами Эйнштейна А21, В21 и В21 можно установить, предполагая, что внутри полости, представляющей абсолютно чёрное тело, находится система атомов при температуре Т. Пусть система атомов имеет два уровня энергии ε2 и ε1 , при переходах между которыми излучается или поглощается квант энергии hν21. При термодинамическом равновесии в системе не происходит изменения энергии, поэтому число излучённых квантов должно быть равно числу поглощённых. Следовательно, в единицу времени во всей системе общее число переходов из верхнего энергетического состояния в нижнее должно быть равно общему числу переходов из нижнего в верхнее: n21=n12. В состоянии равновесия в системе имеется равновесная плотность поля излучения uν, которая определяет число вынужденных переходов в системе. Полное число переходов сверху вниз n21в состоянии равновесия определяется суммой числа спонтанных переходов n21(с) и вынужденных переходов с излучением энергии n21(в), n21=n21(с)+n21(в)=(A21+B21uν)N2. Число переходов n12 снизу вверх определяется только вынужденными переходами с поглощением. n12=n12(в)=B12uνN1. 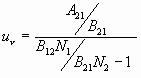Приравнивая на основании n21 и n12 получаем B12uνΝ1=(A21+B21uν)N2 Из этого найдём равновесную плотность энергии поля Соотношение населенностей уровней в состоянии термодинамического равновесия определяется законом Больцмана. N2б/N1б=(g2/g1)exp[-(ε2-ε1)/κΤ], где g1 и g2 -статистический вес уровней; κ - постоянная Больцмана; Т- абсолютная температура. Для невырожденных уровней (g¹=g²=1) закон Больцмана принимает более простую форму записи N2б/N1б=exp[-(ε2-ε1)/κΤ], которая будет далее использоваться. Учитывая, что ε2 - ε1 = hν21, получаем Эйнштейн постулировал, что равновесная спектральная плотность энергии поля должна быть равна её значению, рассчитанному по формуле Планка для равновесного излучения абсолютно чёрного тела: если вместо hν подставить hν21. Сравнивая с учётом этого, получаем условия тождественности этих формул: B12=B21, A21=(8πhν³21/c³)B21. Таким образом, если квантовая система и поле излучения находятся в состоянии термодинамического равновесия, то вероятности вынужденных переходов в единицу времени при единичной плотности полей В12и В21 должны быть одинаковы. Вероятность спонтанных переходов пропорциональна третьей степени частоты перехода, поэтому спонтанное излучение сильнее всего проявляется в оптическом диапазоне волн. Безызлучательные переходы. Атомы и молекулы газа в результате неупругих соударений друг с другом или с электронами теряют или приобретают энергию. При этом энергия электромагнитного поля не излучается, не поглощается. Такие энергетические переходы принято называть безызлучательными. В твёрдом теле безызлучательные переходы происходят вследствие колебательного движения кристаллической решетки. Безызлучательные переходы характеризуются также вероятностью перехода между уровнями j и i сверху вниз ωјі и снизу вверх ωіј соответственно с потерей и получением порции энергии В соответствии с принципами детального равновесия в состоянии термодинамического равновесия подобно число безызлучательных переходов с уровня ј на уровень і в 1 с равно числу обратных безызлучательных переходов с уровня і на уровень ј: ωјіΝј=ωіјΝі. В состоянии термодинамического равновесия распределение населённостей определяется законом Больцмана. ωјі/ωіј = exp (hνјі/κΤ), Из чего следует, что вероятность безызлучательных переходов сверху вниз больше, чем снизу вверх, т.е. ωјі>ωіј ј>і, в отличие от вероятностей вынужденных переходов, которые одинаковы ( Wji = Wij). Если hνјі<<κΤ, что обычно справедливо для квантовых приборов СВЧ диапазона, то можно заменить выражением ωјі/ωіј=1+hνјі/κΤ. Релаксационные переходы. Изолированная система, в которой распределение частиц по энергии отличается от равновесного, называется неравновесной. Неравновесное состояние наблюдается при внешнем воздействии, после прекращения которого система возвращается в равновесное состояние. Процесс установления равновесия в системе называется релаксацией, а переходы частиц с одного уровня на другой в процессе релаксации - релаксационными переходами. В основе процесса релаксации лежит взаимодействие частиц (электронов, атомов, молекул, ионов) между собой и со стенками объёма. Рассмотренные безызлучательные переходы являются релаксационными. К релаксационным переходам следует отнести и спонтанные, роль которых в оптическом диапазоне. Рекласационные переходы приходится учитывать при рассмотрении процессов, выводящих систему из равновесного состояния. При постоянном внешнем воздействии возможна компенсация релаксационных процессов, тогда система будет находится в стационарном неравновесном состоянии. Релаксационные переходы влияют также на ширину спектральной линии. назад | оглавление | вперёд