8.3 Ширина спектральной линии. Естественная ширина спектральной линии. До сих пор предполагалось, что энергетические уровни бесконечно узкие. Однако даже в идеализированном случае, когда на частицу не действуют внешние силы, ширина энергетических уровней кончена. Другими словами, изучение для данного перехода не монохроматическое, а имеет некоторый спектр частот. Зависимость интенсивности излучения от частоты называют спектральной линией излучения, а графическое изображение её – контуром спектральной линии. Минимальная ширина уровней, а, следовательно, и минимальная ширина спектральной линии определяется соотношением неопределённостей Гейзенберга, которое в данном случае лучше записать в виде ∆ε ∆t≥h где ∆ε и ∆t - неопределённости энергии и времени. Предположим, что необходимо определить частоту излучения при переходе с уровня 2 на основной уровень 1. Время жизни частиц в возбуждённом состоянии определяется τ2=1/A21. Следует считать, что неопределённость времени равна времени жизни частиц, т.е. Δt=τ2. Подставляя Δt, получаем неопределённость энергии уровня 2 Δε2>h/τ2. Неопределённость энергии любого уровня j Δ εј>h/τј, где τј – время жизни частицы на уровне ј, определяемое по вероятностям спонтанных переходов с него на нижние уровни. Соотношение определяет зависимость ширины любого энергетического уровня от среднего времени жизни частиц на этом уровне. Если последнее бесконечно велико, то неопределённость энергии, или ширина уровня, бесконечно мала. 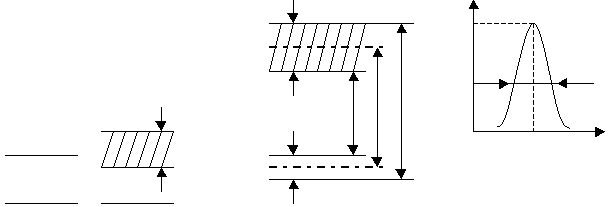Рис. 8.3 Такими будут основной энергетический уровень, нижний уровень системы. Наиболее широкими оказываются уровни с малым временем жизни. Неопределённость частоты перехода между “размытыми” уровнями и с ширинами и находятся из соотношения и определяется суммой неопределённостей энергии обоих уровней. Ширина спектральной линии изолированного и неподвижного атома, определяемая только временем жизни естественной шириной спектральной линии. Ширину контура спектральной линии принято определять как разность частот, на которых интенсивность равна половине максимального значения. Частотой перехода называют частоту, соответствуюшую максимуму спектральной линии. Форма спектральной линии может быть представлена так называемой лоренцевой кривой совпадающей с резонансной кривой колебательного контура. Реальные наблюдаемые спектральные линии имеют ширину больше естественной. Уширение спектральной линии из-за столкновений. В газе происходят упругие и неупругие столкновения частиц. При упругих столкновениях суммарная кинетическая энергия сталкивающихся частиц не изменяется: частицы не обмениваются внутренней энергией и не переходят на другие энергетические уровни. При неупругих столкновениях суммарная кинетическая энергия сталкивающихся частиц либо возрастает, либо убывает. В этом случае изменяется внутренняя энергия сталкивающихся частиц, связанная с электронными, колебательными и вращательными уровнями. В результате неупругих столкновений происходит сокращение времени жизни рассматриваемых частиц в данном энергетическом состоянии до времени среднего пробега между двумя столкновениями, что эквивалентно увеличению ширины спектральной линии. Вероятность столкновений частиц, следовательно, вероятность квантовых переходов одинаковы для частиц газа. Поэтому форма и ширина спектральной линии всего газа и каждой частицы одинаковы, при этом ширина линии газа и частиц стала больше естественной спектральной линии. Такой процесс называют уширением спектральной линии. Однородное уширение наблюдается также в случае столкновения частиц газа со стенками, ограничивающими объём газа. Влияние этих столкновений на ширину спектральной линии становится основным при малом давлении газа, когда вероятность столкновений частиц мала. 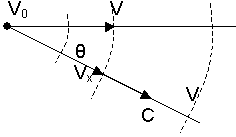Доплеровское уширение спектральной линии. Это уширение связано с эффектом Доплера, т. е. с зависимостью наблюдаемой частоты излучения от скорости движения излучателя. Если источник, создающий в неподвижном состоянии монохроматическое излучение с частотой, движется со скоростью в сторону к наблюдателю так, что проэкция скорости на направление наблюдения составляет, то наблюдатель регистрирует более высокую частоту излучения. где с - фазовая скорость распространения волны; 0 - угол между направлениями скорости излучателя и наблюдения. В квантовых системах источниками излучения являются атомы или молекулы. В газообразной среде при термодинамическом равновесии скорости частиц распределены по закону Максвелла- Больцмана. Поэтому и форма спектральной линии всего вещества – будет связана с этим распределением. В спектре, регистрируемом наблюдателем, должен быть непрерывный набор частиц, так как разные атомы движутся с разными скоростями относительно наблюдателя. 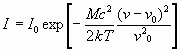Учитывая лишь проекции скорости в распределении Максвелла- Больцмана, можно получить следующее выражение для формы доплеровской спектральной линии: Эта зависимость является гауссовой функцией. Соответствующая значению ширина линии. С увеличением массы частиц М и понижением температуры Т ширина линии уменьшается. Вследствие эффекта Доплера спектральная линия всего вещества не совпадает со спектральной линией отдельной частицы. Наблюдаемая спектральная линия вещества представляет собой суперпозицию спектральных линий всех частиц вещества, т. е. линий с различными центральными частотами. Для лёгких частиц при обычной температуре ширина доплеровской линии в оптическом диапазоне может превышать естественную ширину линии на несколько порядков и достигать значения более1ГГц. Процесс, при котором форма спектральной линии всего вещества не совпадает с формой спектральной линии каждой частицы, называют неоднородным уширением спектральной линии. В рассмотренном случае причиной неоднородного уширения был эффект Доплера. Форма доплеровской спектральной линии описывается гауссовой функцией. Если распределение скоростей частиц отличается от максвелловского, то и форма доплеровской спектральной линии будет отличаться от гауссовой функции, но уширение останется неоднородным. Другие причины уширения спектральной линии. В квантовых приборах широко используют твёрдые вещества с примесными ионами, квантовые переходы которых являются рабочими. Колебания кристаллической решетки модулируют электрическое поле в том месте, где находится ион, и, следовательно, модулируют положение его энергетических уровней и увеличивает ширину спектральной линии. Кроме того, ширина линии увеличивается вследствие тепловых колебаний самих ионов. Причиной уширения спектральной линии твёрдого тела может быть пространственная неоднородность физических параметров среды или неоднородности электрического и магнитного полей. Эти неоднородности будут вызывать неоднородное уширение спектральной линии. Причиной уширения может быть также электромагнитное излучение, вызывающее вынужденные переходы между рассматриваемыми уровнями и приводящее к изменению времени жизни частицы. Поэтому, например, процесс генерации излучения в квантовых приборах будут приводить к изменению ширины линии Спектральные коэффициенты Эйнштейна. Введённые ранее коэффициенты Эйнштейна определяют мощность, излучаемую или поглощаемую во всём спектральном диапазоне данного перехода между ними. Поэтому их называют интегральными коэффициентами Эйнштейна. 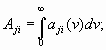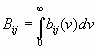Если их необходимо учитывать частотное распределение излучаемой или поглощаемой мощности, то используют спектральные коэффициенты Эйнштейна aji, bji, bij, которые связаны с Аji, Вji и Вij соотношениями Частотная зависимость всех спектральных коэффициентов одинакова и совпадает с формой контура спектральной линии данного перехода – лоренцевой или гауссовой кривыми. Однако с введением коэффициентов а, и следует уточнить также понятие населённости уровней. Под населённостью любого уровня следует понимать частиц в единице объёма, энергия которых попадает в пределы размытости уровня по энергии. Таким образом, число спонтанных и вынужденных переходов в единичном частном интервале вблизи частоты в единицу времени можно записать с использованием дифференциальных коэффициентов Эйнштейна в виде. назад | оглавление | вперёд