8.5 Взаимодействие бегущих электромагнитных волн с активной средой. Предположим, что электромагнитная волна падает на активную среду и распространяется в ней в виде плоской волны по направлению оси. Пусть S - поток энергии через единичное поперечное сечение – изменяется при прохождении излучения через вещество, так как в нём происходят вынужденные переходы с выделением и поглощением энергии. Изменения в слое за 1 с, т. е. изменение мощности. 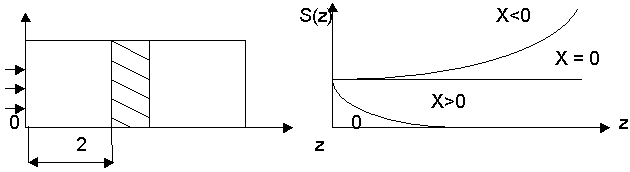Рис. 8.4 Поток энергии связан с объёмной плотностью энергии и групповой скоростью соотношением. Исключая uv , получаем: или где, χ- коэффициентом поглощения. Сначала будем считать, что объемная плотность энергии в веществе на столько мала, что можно пренебречь изменением населенности уровней N1 и N2. Тогда (N1- N2) не зависит от координаты z, т.е. не зависит от z коэффициент χ и интегрирование приводит к формуле: S(z)=S(0)exp(-χz), где S(0)- плотность потока энергии в начале образца (z = 0). Полученная формула называется интегральным законом Бугера. Из уравнения коэффициента поглощения следует, что при N1>N2 (нет инверсии населенностей) и закон описывает поглощение энергии внешнего поля в веществе, а χ имеет смысл коэффициента (показателя) поглощения, показывающего, на кокой длинне энергия волны убывает в е = 2,72 раза. При N2>N1 (инверсия населенностей) χ<0, поэтому отражает усиление поля в веществе. В этом случае говорят об отрицательном коэффициенте поглощения или вводят понятие показатель усиления активной среды: χ а = - χ = Bhυ(N2-N1)/υг. Тогда закон Бугера можно записать S(z)=S(0)exp (χaz) Проведенное рассмотрение не учитывало потерь энергии в среде, пропорциональных проходящей мощности S. Будем считать, что эти потери распределены равномерно по координате z. Тогда дифференциальный закон Бугера можно записать в более общем виде: dS(z)/dz=[χа (υ0)-α]S(z) Потери в активной среде ослабляют усилительный эффект и вызывают ограничение проходящей мощности. С учетом потерь интегральный закон Бугера выглядит так: S(z)=S(0) exp (χa-α)z При увеличении проходящей мощности необходимо учитывать зависимость χа от z. При небольших потерях в активной среде χа=α переходит в χа. В этом случае предельная мощность получается практически при наступлении насыщения перехода. Впред не зависит от входной мощности S(0). На рисунке показана зависимость S(z) при различных значениях S(0): Контрольные вопросы. Виды квантовых переходов. Правило Бора. Понятие о населенностях уровней. Закон Больцмана. Вынужденные переходы частиц между уровнями. Излучательные и безызлучательные переходы. Вероятность перехода и их число. Закон Бугера. Возможность усиления электромагнитных волн веществом. Инверсия населенности уровней. назад | оглавление | вперёд