3 Рассчитать и изобразить на одном графике спектры
|
Теория электрической связи |
|
РАБОТА № 6 |
назад | оглавление | вперёд |
ИЗУЧЕНИЕ ПРИНЦИПА ПЕРЕДАЧИ СИГНАЛОВ ДИСКРЕТНЫМИ ОТСЧЕТАМИ КОТЕЛЬНИКОВА
1 Цель работы
Экспериментальное исследование основных положений теоремы
Котельникова применительно к использованию в технике связи.
2 Литература
[1]-стр.
[2]-стр.
[3]-стр.
[4] Конспект лекций по курсу ТЭС.
[5] Приложение к данной лабораторной работе.
3 Предварительная подготовка к работе
1 Ознакомиться с описанием работы и лабораторным заданием
и изучить по указанной выше литературе следующие вопросы:
а) сущность теоремы Котельникова;
б) структурная схема системы передачи непрерывных сообщений
дискретными отсчетами в соответствии с теоремой Котельникова;
в) амплитудно-частотная, фазо-частотная и импульсная характеристики идеального и реального фильтров нижних частот (ФНЧ);
г) погрешности восстановления реальных сигналов по отсчетам и их
причины.
2 Ответить (устно) на вопросы раздела 4 данной работы;
3 Рассчитать и изобразить на одном графике спектры ![]() одиночных видеоимпульсов прямоугольной формы с амплитудой А=1В и длительностью
одиночных видеоимпульсов прямоугольной формы с амплитудой А=1В и длительностью
![]() 0
,2 ;
0
,4 ;
0
,6
мс в диапазоне частот
0
,2 ;
0
,4 ;
0
,6
мс в диапазоне частот ![]()
![]()
![]()
![]()
![]() .
.
Ограничивая ширину спектра видеоимпульса первым нулем огибающей
спектральной плотности, определить для каждого случая требуемую частоту
отсчетных импульсов, удовлетворяющую условию теоремы Котельникова.
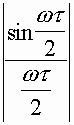
Спектральная плотность одиночного видеоимпульса определяется
соотношением
![]()
4 Изучить описание лабораторной установки и лабораторное задание.
5 Продумать порядок выполнения работы в лаборатории, нарисовать структурные
схемы измерений и подготовить необходимые таблицы и графики для каждого пункта
лабораторной работы.
4 Вопросы для самостоятельной подготовки
1. Сформулируйте теорему Котельникова. Поясните ее сущность
на примере некоторой непрерывной функции.
2. Нарисуйте упрощенную структурную схему передачи непрерывных
сообщений в соответствии с теоремой Котельникова с приведением временных
и спектральных диаграмм в различных характерных точках тракта.
3. Запишите ряд Котельникова и дайте его пояснение.
4. Объясните принцип восстановления сигнала по отсчетам Котельникова с помощью
идеального ФНЧ.
5. Приведите выражения и графики амплитудно-частотной и
фазо-частотной характеристик идеального ФНЧ.
6. Приведите выражение, описывающее импульсную характеристику
идеального ФНЧ, и изобразите график.
7. Объясните, в чем отличие характеристик реальных фильтров нижних частот от
идеального ФНЧ.
8. Объясните причины погрешности восстановления реальных сигналов
по дискретным отсчетам.
9. Изобразите график спектра импульсной последовательности дискретных отсчетов.
10. Как зависит погрешность восстановления сигнала от числа членов ряда Котельникова,
учитываемых пределами суммирования?
11. Запишите обратное преобразование Фурье для сигнала с ограниченным
спектром.
12. Приведите пару преобразований Фурье для связи импульсной характеристики
фильтра и комплексного коэффициента передачи.
13. Из какого условия ограничивают ширину спектра сигналов, передаваемых по
каналам связи отсчетами Котельникова, для определения верхней
частоты спектра ![]() ?
?
14. Изобразите и объясните спектр сигнала на выходе импульсного
модулятора при передаче дискретными отсчетами Котельникова некоторого
непрерывного сообщения с заданным спектром.
15. Проанализируйте характер зависимости между скоростью изменения временной
функции сигнала и шириной его спектра. Каким образом можно
качественно оценить и сравнить между собой требуемую частоту следования
отсчетных импульсов по виду временных диаграмм двух различных сигналов?
5 Описание лабораторной установки
Лабораторная установка, краткое описание которой приведено
на стр. 5-10, позволяет исследовать упрощенную структурную схему передачи различных
сообщений с ограниченным спектром дискретными отсчетами
в соответствии с теоремой Котельникова. На рисунке 6.1 показана структурная
схема соединения блоков макета системы связи с учетом обозначений на передней
панели макета (рисунок 0.2). В качестве передаваемых сигналов используются простые
сигналы вида гармонического колебания различной частоты и периодической последовательности
прямоугольных импульсов различной длительности. Выбор такой формы исследуемых
сигналов для изучения использования теоремы Котельникова в технике связи объясняется
соображениями простоты их получения, например, с помощью типовой измерительной
аппаратуры. В то же время это не снижает общности результатов лабораторного
эксперимента, так как используемые в работе сигналы можно считать частным случаем
реальных сигналов.
Для изучения восстановления сигналов по отсчетам Котельникова,
оценки погрешностей восстановления в макете используется амплитудно-импульсный
модулятор (АИМ) и ![]() -
фильтр в качестве ФНЧ. В качестве
-
фильтр в качестве ФНЧ. В качестве
генератора импульсов отсчета используется блок ²
дискретный шум² .
При снятии амплитудно-частотной характеристики ![]() -
фильтра нижних частот измерительный сигнал на его вход подается от внешнего
звукового
-
фильтра нижних частот измерительный сигнал на его вход подается от внешнего
звукового
генератора, а уровень сигнала на выходе фильтра измеряется с помощью милливольтметра.
Наблюдение осциллограмм исследуемых сигналов производится
с помощью осциллографа С1-72.
Изменение вида сообщения и его параметров осуществляется путем установки переключателей на передней панели лабораторного макета в требуемое положение.
Рисунок 6.1-Структурная схема лабораторной установки
6 Лабораторное задание
1. Ознакомиться с используемыми в работе измерительными приборами
и лабораторной установкой, изучить её структурную схему, отгравированную
на передней панели (мнемосхему), расположение органов управления и порядок пользования
ими.
2. Снять и построить амплитудно-частотную и импульсную характеристики ![]() -
фильтра нижних частот.
-
фильтра нижних частот.
3. Изучить принцип передачи различных сообщений с ограниченным спектром дискретными
отсчетами по Котельникову путем получения и зарисовки осциллограмм сигналов
в различных точках структурной схемы системы передачи сообщений. Исследовать
влияние характеристик ФНЧ на точность
восстановления сигнала по отсчетам Котельникова.
7 Порядок выполнения работы
1. Включить лабораторную установку и приборы.
2.Снять и построить амплитудно-частотную характеристику
![]()
![]() - фильтра нижних частот. Для этого установкой переключателей в необходимое положение
собрать схему исследования в соответствии со схемой соединений функциональных
блоков макета системы связи, приведенной на рисунке 6.1.
- фильтра нижних частот. Для этого установкой переключателей в необходимое положение
собрать схему исследования в соответствии со схемой соединений функциональных
блоков макета системы связи, приведенной на рисунке 6.1.
Измерительный сигнал на вход ФНЧ (Ф1) подается от внешнего звукового генератора, который должен быть подключен к гнезду “ВНЕШ.” в блоке “непрерывное сообщение”, кнопка “ВНЕШ.” нажата. Уровень сигнала на выходе генератора установить равным 2В, наличие сигнала на входе ФНЧ контролируется осциллографом в гнезде Г9. Уровень сигнала на выходе фильтра измеряется милливольтметром в гнезде Г10.Рекомендуемый диапазон изменения частоты 20, 100-1000 Гц (с шагом 100 Гц).Построить АЧХ фильтра
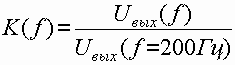
и определить по ней граничную частоту (частоту среза ![]() .)
ФНЧ, т.е. частоту, при которой коэффициент передачи фильтра равен 0,5.
.)
ФНЧ, т.е. частоту, при которой коэффициент передачи фильтра равен 0,5.
3. Получить и зарисовать осциллограмму импульсной характеристики
ФНЧ ![]() .
Для этого на вход ФНЧ должны поступать импульсы длительностью 1мс, амплитудой
3,5В и периодом следования 12 мс. Для формирования такого импульсного сигнала
необходимо: тумблер П1
.
Для этого на вход ФНЧ должны поступать импульсы длительностью 1мс, амплитудой
3,5В и периодом следования 12 мс. Для формирования такого импульсного сигнала
необходимо: тумблер П1
установить в положение 1, нажать кнопку “код 2”, тумблеры 1-4 в блоке “дискретное
сообщение” выключить, ключить тумблер “1” в блоке “дискретный шум” (остальные
тумблеры 2-7 выключены).
Вид импульсной характеристики на выходе ФНЧ (гнездо Г10) наблюдать
на экране осциллографа в режиме внутренней синхронизации (кнопка “Внутренняя
синхронизация” нажата) и при чувствительности по входу “![]() ”
0,5 Вольт/дел. Получить устойчивую осциллограмму (ручками “стабильность”
”
0,5 Вольт/дел. Получить устойчивую осциллограмму (ручками “стабильность”
и “уровень”) и зарисовать ![]() .
Определить время запаздывания максимума выходного напряжения фильтра, используя
масштаб калиброванной развертки осциллографа.
.
Определить время запаздывания максимума выходного напряжения фильтра, используя
масштаб калиброванной развертки осциллографа.
4. Изучить экспериментально принцип передачи сообщений
дискретными отсчетами по Котельникову и восстановления сигналов
по отсчетам на приеме.
4.1 Собрать схему для случая передачи непрерывного сообщения типа гармонического колебания. Для этого необходимо получить сигнал амплитудно-импульсной модуляции (АИМ) и подать его на вход фильтра нижних частот. Гармоническое колебание на модулятор АИМ подается от внешнего звукового генератора (подключенного ко входу “ВНЕШ.” и при нажатой кнопке “ВНЕШ.” Блока “непрерывное сообщение”) через тумблер П1 (положение 2) и далее через тумблер П2 (положение 1). Импульсный модулятор включается нажатием кнопки АИМ, все тумблеры на блоке “дискретный шум” должны быть выключены.
На вход амплитудно-импульсного модулятора кроме гармонического
сигнала подается постоянное напяжение от внутреннего источника. Уровень сигнала
следует взять порядка 2В. На выходе АИМ наблюдается прямая линия “нуля” и положительные
импульсы (на осциллографе видны только плоские вершины) с частотой дискретизации
1200 Гц. Частоту сигнала следует взять равной 200-300 Гц. Огибающая отcчетов
будет иметь форму синусоиды
без ограничения (отсечки) снизу, иначе следует уменьшать уровень сигнала.
Зарисовать осциллограммы напряжений на выходе модулятора АИМ
(в гнезде Г4 или на на входе ФНЧ в гнезде Г9) и на выхода ![]() -
фильтра нижних частот при частотах 300, 600 и 900 Гц. При этом осциллограф должен
работать
-
фильтра нижних частот при частотах 300, 600 и 900 Гц. При этом осциллограф должен
работать
в режиме внутренней синхронизации – кнопка "Внутренняя синхронизация"
нажата.
При снятии осциллограмм на выходе ФНЧ на частоте вблизи 600 Гц обратить внимание на возникновение биений. При исследовании восстановления сигнала с частотой 900 Гц сравнить частоты сигналов на входе АИМ и на выходе ФНЧ.
Обратите внимание на изменение уровня на выходе ФНЧ при изменении его на входе АИМ.
4.2 Собрать схему для случая передачи импульсного сигнала, для чего: тумблер П1 установить в положение 1, включить все тумблеры в блоке "дискретное сообщение". При этом на вход ФНЧ будет поступать сигнал АИМ дискретного (импульсного) сообщения. Устанавливая тумблеры 1-7 в блоке "дискретный шум" в различные положения (часть включена-подряд, а остальные выключены), получить 2, 4 и 7 отсчетных импульсов.
Зарисовать осциллограммы на входе и выходе ФНЧ в режиме внешней синхронизации осциллографа.
8 Содержание отчета
Отчет должен содержать результаты предварительной подготовки
к работе, структурную схему соединения блоков лабораторной установки
для данной работы, результаты измерений в виде таблиц, графиков и осциллограмм
с соответствующими заголовками, исходными данными и пояснениями, краткие выводы
и оценку результатов.
Приложение 6.1
ТЕОРЕМА КОТЕЛЬНИКОВА
В соответствии с теоремой Котельникова сигнал, описываемый
непрерывной функцией ![]() с ограниченным спектром, полностью определяется своими значениями
с ограниченным спектром, полностью определяется своими значениями ![]() отсчитанными через интервалы времени
отсчитанными через интервалы времени 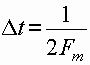 ,
где
,
где ![]() - ширина спектра сигнала.
- ширина спектра сигнала.
Для техники связи очень важна такая возможность представления
непрерывного случайного сигнала через совокупность его значений в дискретные
моменты времени. Действительно, нет необходимости передавать все значения непрерывной
функции времени, а достаточно посылать лишь его мгновенные значения с постоянной
скоростью ![]() .
Дискретизация непрерывных сообщений составляет основу построения систем передачи
аналоговой информации цифровыми методами.
.
Дискретизация непрерывных сообщений составляет основу построения систем передачи
аналоговой информации цифровыми методами.
В настоящее время все страны осуществляют переход на цифровую
сеть интегрального обслуживания (ЦСИО - ![]() ).
В основе построения такой
).
В основе построения такой
сети лежит импульсно-кодовая модуляция (ИКМ), базирующаяся на теореме
Котельникова.
Важно помнить, что реальных сигналов со строго ограниченным
спектром не существует, так как сигналы конечной длительности имеют бесконечные
частотные спектры. В то же время конечная полоса пропускания каналов связи требует
ограничения спектра передаваемых сообщений. Практически ширину спектра исходного
сообщения ограничивают некоторой верхней частотой ![]() так, чтобы в диапазоне частот 0…
так, чтобы в диапазоне частот 0…![]() была сосредоточена основная часть энергии сигнала (
была сосредоточена основная часть энергии сигнала (![]() ).
Эту полосу частот принято называть практической шириной спектра
).
Эту полосу частот принято называть практической шириной спектра ![]() ,
а спектром сигнала для частот
,
а спектром сигнала для частот ![]() пренебрегают.
пренебрегают.
В основе математического описания временной дискретизации непрерывных
сообщений (сигналов) лежит периодическая последовательность
![]() -импульсов
с периодом
-импульсов
с периодом ![]() .
Следовательно, взятие отсчетов
.
Следовательно, взятие отсчетов
исходного сообщения эквивалентно умножению его временной функции на последовательность
![]() -импульсов.
Дискретизированная функция передаваемого сообщения будет представлять собой
не что иное, как сигнал амплитудно-импульсной модуляции (АИМ).
-импульсов.
Дискретизированная функция передаваемого сообщения будет представлять собой
не что иное, как сигнал амплитудно-импульсной модуляции (АИМ).
Процедура преобразования непрерывного сообщения ![]() в последовательность отсчетов по Котельникову
в последовательность отсчетов по Котельникову ![]() поясняется временными и спектральными диаграммами, приведенными на рисунках
6.2 и 6.3.
поясняется временными и спектральными диаграммами, приведенными на рисунках
6.2 и 6.3.
Отсчеты исходного сообщения могут быть переданы на противоположную сторону любым способом. На приемной стороне системы связи осуществляется восстановление исходного сообщения по принимаемой последовательности отсчетов.
В соответствии с рядом Котельникова непрерывная функция является
разложением ее в ряд по ортогональной системе функций отсчета вида ![]() :
:
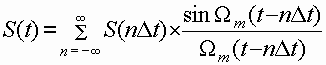 (6.1)
(6.1)
Рисунок 6.2-Представление непрерывного сигнала
последовательностью отсчетов
Рисунок 6.3-Спектральное представление дискретизированного сигнала
Таким образом, ряд Котельникова указывает на способ восстановления
исходного сообщения по последовательности отсчетов путем формирования для каждого
отсчета ![]() функции
функции  с соответствующей амплитудой и последующим суммированием всех функций. Техническим
устройством, которое на воздействие в виде дельта-функции формирует отклик вида
с соответствующей амплитудой и последующим суммированием всех функций. Техническим
устройством, которое на воздействие в виде дельта-функции формирует отклик вида
![]() , является
идеальный фильтр нижних частот (ФНЧ) с полосой пропускания равной
, является
идеальный фильтр нижних частот (ФНЧ) с полосой пропускания равной ![]() .
.
Процесс восстановления исходной функции по последовательно
сти отсчетов на приемной стороне показан на рисунке 6.4. На вход фильтра поступают
через интервалы времени ![]() короткие импульсы с амплитудами, соответствующими (пропорциональными) отсчетам
короткие импульсы с амплитудами, соответствующими (пропорциональными) отсчетам
![]() . Напряжение на выходе
фильтра будет представлять собой сумму откликов фильтра на каждый из входных
импульсов. Причем, в моменты времени
. Напряжение на выходе
фильтра будет представлять собой сумму откликов фильтра на каждый из входных
импульсов. Причем, в моменты времени ![]() только один из откликов
только один из откликов
(на данный импульс) не равен нулю и максимален, а отклики от всех других
импульсов отсчета равны нулю. В остальные промежуточные моменты времени ![]()
![]()
![]()
![]()
![]() суммируется бесконечное количество откликов.
суммируется бесконечное количество откликов.
При практическом использовании теоремы и ряда Котельникова
для восстановления непрерывного сообщения по дискретным отсчетам неизбежно будут
возникать погрешности восстановления, обусловливающие отличие принятого сообщения
![]() от передаваемого
от передаваемого ![]() .
Наиболее важной причиной этого является отличие характеристик реальных ФНЧ от
идеального.
.
Наиболее важной причиной этого является отличие характеристик реальных ФНЧ от
идеального.
1 У идеального фильтра нижних частот амплитудно-частотная характеристика
![]() имеет прямоугольную форму,
т.е.
имеет прямоугольную форму,
т.е.
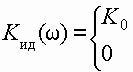
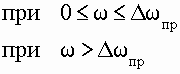 (6.2)
(6.2)
а фазо-частотная характеристика ![]() - линейна. То есть идеальный ФНЧ с одинаковым коэффициентом передачи пропускает
все частотные составляющие спектра входного сигнала в пределах полосы пропускания
- линейна. То есть идеальный ФНЧ с одинаковым коэффициентом передачи пропускает
все частотные составляющие спектра входного сигнала в пределах полосы пропускания
![]() и
и
полностью отфильтровывает (подавляет) составляющие с частотами ![]() .
.
Реализовать фильтр с формой АЧХ (6.2) практически невозможно.
У реальных фильтров нижних частот АЧХ не обеспечивает резкого ограничения спектра
на граничной частоте среза фильтра ![]() ,
а имеет наклонный участок определенной крутизны. Следовательно, в полосу пропускания
фильтра
,
а имеет наклонный участок определенной крутизны. Следовательно, в полосу пропускания
фильтра
будут попадать и спектральные составляющие части спектра дискретизированного
сигнала с поднесущей ![]() (рисунок 6.3,б). Кроме того, АЧХ реальных ФНЧ имеют также и заметную неравномерность
в пределах полосы пропускания. Все это приведет к искажению формы сигнала на
выходе ФНЧ, т.е. к увеличению ошибки восстановления.
(рисунок 6.3,б). Кроме того, АЧХ реальных ФНЧ имеют также и заметную неравномерность
в пределах полосы пропускания. Все это приведет к искажению формы сигнала на
выходе ФНЧ, т.е. к увеличению ошибки восстановления.
2 Неидеальность АЧХ и ФЧХ реальных ФНЧ будут вызывать и неполное совпадение их импульсной характеристики
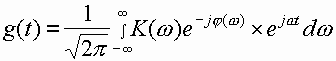 (6.3)
(6.3)
с функцией вида 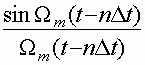 в моменты времени
в моменты времени ![]() .
Это приводит
.
Это приводит
к тому, что сигнал на выходе фильтра в моменты времени ![]() определяется
определяется
не одним отсчетом, а всеми (многими) предшествующими.
Рисунок
6.4-Процесс восстановления сигнала по отсчетам ![]()
3 Реальные фильтры имеют конечную "память" (конечное время
запаздывания сигнала на выходе относительно входного ![]() -импульса)
и, следовательно, будут суммировать одновременно конечное число отсчетов (вместо
бесконечного в случае идеального ФНЧ). Это является причиной увеличения ошибки
-импульса)
и, следовательно, будут суммировать одновременно конечное число отсчетов (вместо
бесконечного в случае идеального ФНЧ). Это является причиной увеличения ошибки
восстановления.
Количественно погрешность восстановления, характеризующую степень
несоответствия восстановленного сообщения ![]() исходному переданному
исходному переданному ![]() ,
оценивают величиной относительной среднеквадратической ошибки
,
оценивают величиной относительной среднеквадратической ошибки
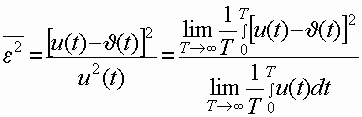 (6.4)
(6.4)
В частном случае при восстановлении прямоугольного импульса
длительностью ![]() ошибка будет
определяться выражением
ошибка будет
определяться выражением
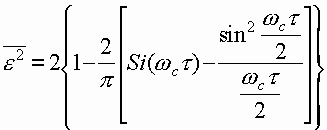 (6.5)
(6.5)
где 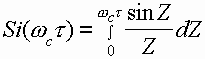 - интегральный синус,
- интегральный синус, 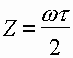 .
.
назад | оглавление | вперёд