| Цифровая обработка сигналов |
| Часть1 §1 Дискретизация непрерывных сигналов |
назад | оглавление | вперёд |
Возникновение ЦОС – пятидесятые годы. В это время ЭВМ впервые стали применяться для моделирования аналоговых (непрерывных) сигналов (моделирование может быть использовано для обработки реальных сигналов). Для этого сигнал записывался на магнитную ленту и потом обрабатывался на ЭВМ. Время обработки измерялось в часах, время записи – в секундах.
В шестидесятые годы изобретен алгоритм Фурье, быстрое преобразование Фурье. В результате свертку сигнала можно было заменить произведением спекторов этих сигналов, что ускоряло обработку сигналов на несколько порядков и в результате появляется возможность обработки сигналов в реальном масштабе времени.
В семидесятые и восьмидесятые годы развитие микроэлектроники позволило запараллеливать вычислительные операции (развернуть процесс в пространстве). В результате скорость обработки сигналов резко возросла и процесс обработки сигналов стали более широкополосным. ЦОС в настоящее время применяется в различных областях техники, где она нужна.
§1 Дискретизация непрерывных сигналов.
Цифровые системы связи вырабатывают дискретные сигналы, которые получаются из непрерывных путем дискретизации.
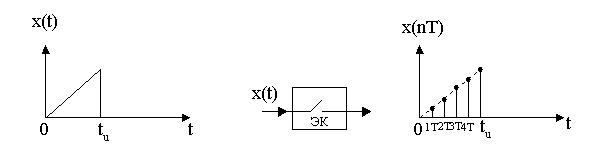
Схема дискретизации:
![]()
![]()
![]()
![]()
fg – частота дискретизации
Т – интервал дискретизации![]()
X(t) – непрерывный (аналоговый) сигнал
X(nТ) – дискретный сигнал
X(nТ) = X(n) = Xn = {X0; X1; X2; … } – обозначения дискретного сигнала.
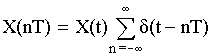 – формула связи дискретного и аналогового
сигналов.
– формула связи дискретного и аналогового
сигналов.
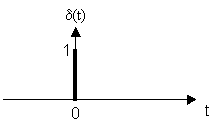
![]() – дискретная
– дискретная ![]() – функция.
– функция.
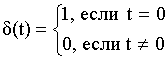
![]() – периодическая последовательность
– периодическая последовательность
![]() – функции, следующая с интервалом T.
– функции, следующая с интервалом T.
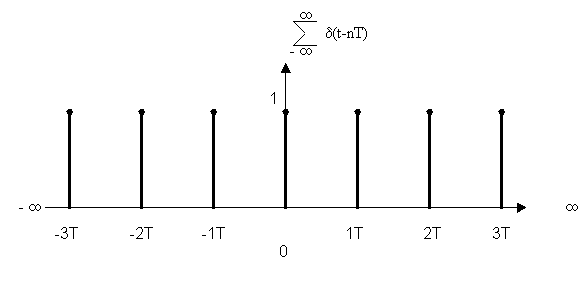
![]()
§2 Связь спектров дискретных и непрерывных сигналов.
Пусть ![]()
![]() – спектр дискретного сигнала x(nТ);
– спектр дискретного сигнала x(nТ);
![]() (jω) – спектр исходного аналогового сигнала x(t).
(jω) – спектр исходного аналогового сигнала x(t).
Для установления связи между спектрами воспользуемся
прямым преобразованием Фурье: ![]()
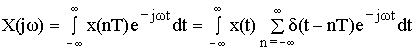
Раскладываем в ряд Фурье:
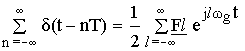
Fl – амплитуда гармоник.
Определим Fl используя формулу связи между спектрами периодических и непериодических сигналов.
![]()
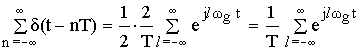
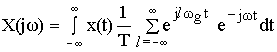
В силу линейности операции в этом выражении знаки
![]() и
и ![]() можно поменять местами.
можно поменять местами.
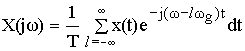
Воспользуемся теоремой смещения (теорема о спектрах).
Если 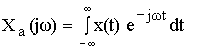 , то:
, то:
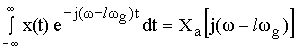
Формула связи спектров дискретного и аналогового сигналов имеет вид:
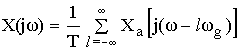
Вывод: спектр дискретного сигнала равен сумме
равно-смещенных спектров аналогового сигнала, сдвинутых на величину кратных
![]() .
.
Полученный результат продемонстрируем на графиках.
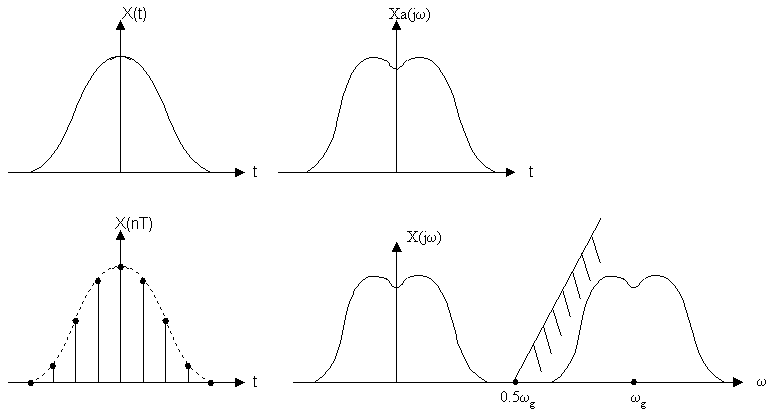
Если ![]() , то спектр дискретного и аналогового сигналов
совпадает (X(jω) и Xa(jω)
совпадают) на интервале [-0.5ωg;0.5ωg].
В результате x(t) аналоговый сигнал можно восстановить применением ФНЧ с частотой
среза ωс=0.5ωg.
, то спектр дискретного и аналогового сигналов
совпадает (X(jω) и Xa(jω)
совпадают) на интервале [-0.5ωg;0.5ωg].
В результате x(t) аналоговый сигнал можно восстановить применением ФНЧ с частотой
среза ωс=0.5ωg.
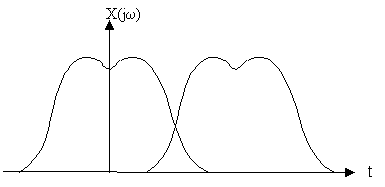
Если ωв>0.5ωg, то смежные спектры перекрываются и возникают ошибки
наложения, погрешности (не устранимые), поэтому восстановить такой сигнал
можно только с искажением (искажения могут оказаться значительными).
§3 Преобразования Фурье и Лапласа для дискретных сигналов.
Формула Фурье для дискретного сигнала:
![]()
![]() – прямое преобразование Фурье.
– прямое преобразование Фурье.
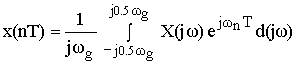 – обратное преобразование Фурье.
– обратное преобразование Фурье.
Сигнал x(nT) нормирован по отношению к X. ![]()
После денормирования сигнала формулу записываем в виде:
![]()
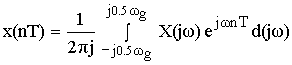
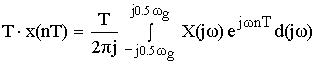
Устремляем T к нулю.
Если ![]() , то T вырождается
в непрерывную переменную
, то T вырождается
в непрерывную переменную ![]()
Денормированные формулы прямого и обратного преобразования Фурье для непрерывных сигналов:
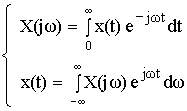
Это доказывает справедливость формулы Фурье для дискретного
сигнала. Переменную ω можно распространить на всю плоскость комплексного
переменного: ![]()
![]() , и тогда формулы Фурье для дискретного
сигнала заменяются формулами Лапласа.
, и тогда формулы Фурье для дискретного
сигнала заменяются формулами Лапласа.
![]()
![]()
![]() – прямое преобразование.
– прямое преобразование.
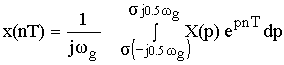 – обратное преобразование.
– обратное преобразование.
Изображение по Лапласу дискретных сигналов X(p) является функцией трансцендентной, что значительно затрудняет частотный анализ дискретных сигналов. Переменную p, находящуюся в показателе экспоненты, заменяют:
![]()
![]() X(p)
заменяется на рациональную функцию, что упрощает частотный анализ.
X(p)
заменяется на рациональную функцию, что упрощает частотный анализ.
X(Z) – Z-изображение дискретного сигнала x(nT).
Если в формулах Лапласа сделать замену:
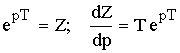
В результате получаем формулы Z-преобразования:
![]() – прямое Z-преобразование.
– прямое Z-преобразование.
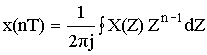 – обратное Z-преобразование.
– обратное Z-преобразование.
Рассмотрим особенности перехода от плоскости комплексного переменного p=σ+jω к плоскости комплексного переменного Z=x+jy.
![]() , пусть σ=0, т.е. p=jω
тогда:
, пусть σ=0, т.е. p=jω
тогда:![]()
где 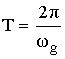
Если ω=0, то Z=1.
Если ω=0.5ωg, то ![]() .
.
Если ω=ωg, то ![]() .
.
При увеличении переменной ω, переменная Z осуществляет многократное перемещение по единичной окружности.
По изображению X(Z) можно получить спектр дискретного сигнала, для этого вместо Z надо подставить:
![]()
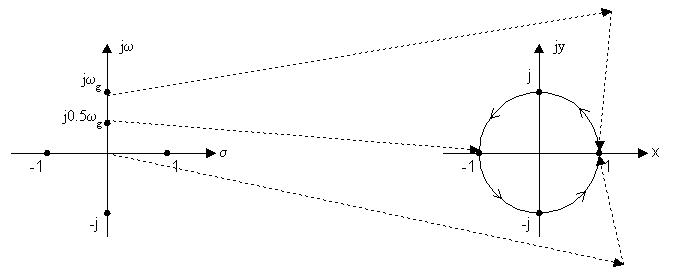
Точкам в левой полуплоскости комплексного переменного p соответствуют значения переменной внутри единичного круга на плоскости Z.
Пример 1:
Определить Z-изображение сигнала.
![]()

![]()
![]()

Пример 2:
Определить спектр сигнала (пример 1).
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

| ω |
0 |
0.5ωg |
ωg |
|
|
0 |
π |
2π |
| sinωT |
0 |
0 |
0 |
| cosωT |
+1 |
-1 |
+1 |
|
|
a+b |
a-b |
a+b |
| φ(ω) |
0 |
0 |
0 |

§5 Основные свойства Z-преобразования.
1.Линейность:
Если ![]() , то
, то ![]() .
.
2.Запаздывание:
Если ![]()
3.Свертка:
Если 
4.Умножение:
Если ![]() , то
, то

V, Z – переменные на плоскости Z.
5.Равенство Парсеваля (теорема энергии):

Дискретное преобразование Фурье (ДПФ).
Если сигнал x(nT) ограничен одновременно по времени некоторым значением tи, и по частоте fв, то он характеризуется конечным числом отсчетов N как во времени, так и в частотных областях.
Во временной области 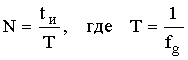 ;
;

В частотной области  – это интервал между смежными отсчетами
спектра.
– это интервал между смежными отсчетами
спектра.
ωg – тактовая частота
![]()
![]()
Отсчеты сигнала x(nT) являются коэффициентами Фурье периодической последовательности X(jω) с периодом ωg. Это следует из формулы прямого преобразования Фурье для дискретных сигналов.
Отсчеты в частотной области (X0,X1,…) тоже являются коэффициентами Фурье периодической последовательности x(t) с периодом tи.
Отсчеты во временной и частотной области связаны между собой формулами ДПФ. Формулы ДПФ следуют из формул для дискретных сигналов.

В этих формулах перейдем к дискретной переменной kω1 от непрерывной переменной ω.

В результате такого перехода исходная пара преобразований принимает вид:


В результате формула принимает вид:

![]() прямое и обратное ДПФ
прямое и обратное ДПФ
Пример:
![]() , где a и b положительные
вещественные числа a>b.
, где a и b положительные
вещественные числа a>b.
Определить отсчеты спектра



В качестве проверки по частотным отсчетам найдем временные.
![]()

![]()
![]()
Обычная аналоговая (RL-цепь) цепь описывается дифференциальными уравнениями. Если непрерывную переменную t заменить на дискретно изменяющуюся переменную nT, то дифференциальные уравнения вырождаются в разностные уравнения. Разностные уравнения общего вида, в котором в явной форме выражены прямые и обратные связи и который связывает сигналы на входе и выходе имеют следующий вид:
 – разностное уравнение общего
вида,
– разностное уравнение общего
вида,
где: x(nT)– сигнал на входе цепи,
y(nT)– сигнал на выходе,
M– число прямых отводов,
(L-1)– число обратных отводов,
m, l– целые числа,
am, bm– вещественные коэффициенты.
Такому уравнению соответствуют цепи, которые называют
дискретной цепью.

 Элемент
запаздывания на время T или элемент памяти.
Элемент
запаздывания на время T или элемент памяти.
 Сумматор.
Сумматор.
Т– интервал дискретизации поступающего сигнала,
ai,bi– умножители на коэффициент ai или bi.
Схема разностной цепи и значение коэффициентов ai и bi определяют способ обработки сигналов, поступающих на вход цепи. Расчет выходного сигнала y(nT) осуществляется путем решения разностного уравнения. Существуют аналитические и численные способы решения разностных уравнений.
Аналитические способы позволяют получить решение в общем виде, сделать анализ. Численные способы дают ответ в виде числовой последовательности.
Разностные уравнения – это алгоритм функционирования дискретной цепи. Разностное уравнение записывается непосредственно по схеме.
Пример: Составить разностное уравнение.

y(nT) = 0.5·x(nT) + (-0.7) ·x(nT-T) + 0.8·x(nT-2T) + 0.2·x(nT-3T)
Пример: Определить y(nT) если x(nT)={1;0.5} для цепи:

y(nT) = 0.1·x(nT) + 0.5·x(nT-T)
Воспользуемся численным методом.
n=0; y(0T) = 0.1·x(0T) + 0.5·x(-T) = 0.1 + 0.5·0 = 0.1
n=1; y(1T) = 0.1·x(1T) + 0.5·x(0T) = 0.1·0.5 + 0.5·1 = 0.55
n=2; y(2T) = 0.1·x(2T) + 0.5·x(1T) = 0.1·0 + 0.5·0.5 = 0.25
n=3; y(3T) = 0.1·x(3T) + 0.5·x(2T) = 0.1·0 + 0.5·0 = 0
y(nT) = {0.1; 0.55; 0.25}
Пример: Определить сигнал на выходе, если x(nT) = {1; 1}

Цепь с обратной связью.
Составим разностное уравнение из двух слагаемых:
y(nT) = 0.4·x(nT-T) – 0.2·0.4·y(nT-T)
вх.сигнал вых.сигнал
n=0; y(0T) = 0.4·x(-T) – 0.08·y(-T) = 0, где: x(-T) = y(-T) = 0
n=1; y(1T) = 0.4·x(0T) – 0.08·y(0T) = 0.4·x(T-T) – 0.08·y(T-T) = 0.4·1-0.08·0 = = 0.4
n=2; y(2T) = 0.4·x(1T) – 0.08·y(1T) = 0.4·1 – 0.08·0.4 = 0.4 – 0.032 = 0.368
n=3; y(3T) = 0.4·x(2T) – 0.08·y(2T) = 0.4·0 – 0.08·0.368 = –0.02944
n=…
y(nT) = {0; 0.4; 0.368; –0.2944; …}
Цепь дискретная, содержащая обратную связь, называется рекурсивной, а цепь, не содержащая обратной связи, называется не рекурсивной.
§8 Алгебраизация разностных уравнений.
Разностные уравнения становятся алгебраическим уравнением, если сигналы заменить их Z-изображениями.
Рассмотрим это на примере общего вида:

X(nT) Þ X(Z), y(nT) Þ Y(Z)
x(nT–mT) Þ X(Z)·Z-m,
y(nT–lT) Þ Y(Z)·Z-l
В результате теоремы линейности получим:
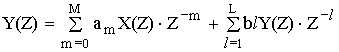 алгебраическое уравнение относительно
Z.
алгебраическое уравнение относительно
Z.
Алгебраическое уравнение существенно проще разностного уравнения.
В результате эффективность анализа расчета становится выше.
§9 Передаточная функция дискретной цепи.
Передаточная функция дискретной цепи определяется отношением:

Получим выражение общего вида для передаточной функции дискретной цепи. Для этого используем алгебраическое уравнение общего вида:



 передаточная функция рекурсивной
цепи общего вида.
передаточная функция рекурсивной
цепи общего вида.
 передаточная функция не рекурсивной цепи
общего вида.
передаточная функция не рекурсивной цепи
общего вида.
Найдем передаточную функцию элемента запаздывания:

y(nT) = x(nT–T)
Y(Z) = X(Z)·Z-1 H(Z) = Z-1
Передаточная функция дискретной цепи определяется непосредственно по схеме, теми же методами, что и цепи RLC.
Для цепи с обратной связью используется формула:

Hyc(Z)–передаточная функция участка цепи прямого прохождения сигнала.
Hoc(Z)–передаточная функция обратной связи .
Пример 1: Определить передаточную функцию цепи.

H(Z) = 0.5 + 0.3·Z-1– 0.8·Z-2
Пример 2: Определить передаточную функцию.



Пример 3: Определить передаточную функцию.

Первый участок цепи рекурсивный, есть обратная связь.

Второй участок цепи нерекурсивный.

§10 Частотные характеристики дискретной цепи.
Частотные характеристики определяются по известному выражению H(Z) для H(Z) общего вида:

Частотные характеристики получаются после замены:
![]()



 – АЧХ.
– АЧХ.
![]() – ФЧХ.
– ФЧХ.
При расчетах и проектировании дискретных цепей вводят нормирование по частоте.
 ; т.е. при ω=0 → Ω=0
; т.е. при ω=0 → Ω=0
при ω= ωg → Ω=1

§11 Общие свойства передаточной функции дискретной цепи.
Для дискретной цепи общего вида передаточная функция является рациональной функцией и записывается так:

Согласно этому выражению можно сделать заключение общего характера: любая рациональная функция от Z может быть реализована в виде дискретной цепи. Передаточная функция, которая совпадает с заданной рациональной функцией с точностью до постоянного множества ZQ при условии, что заданная рациональная функция удовлетворяет следующим требованиям:
1. коэффициенты аi и bi –вещественные числа.
2. Корни уравнения V(Z)=0 расположены в пределах единичного круга на плоскости Z.
Второе замечание касается устойчивости цепи (цепь устойчива если полюсы H(p) расположены в левой полуплоскости комплексной переменной p, но, при переходе к плоскости Z, левая полуплоскость p отображается на единичный круг плоскости Z.
Пример: Задана рациональная функция (дробная):
 Преобразим эту функцию по форме
передаточной функции общего вида.
Преобразим эту функцию по форме
передаточной функции общего вида.

Z4= ZQ
1 + 0.8Z-2 = 0
Z2 + 0.8 = 0
![]()

Цепь устойчивая.

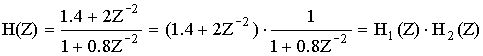



![]()
§12 Импульсная характеристика.
Импульсная характеристика и передаточная функция являются общими характеристиками цепи.
h(nT)– импульсная характеристика,
H(Z)– передаточная функция.
Обе характеристики связаны Z–преобразованиями.
При проектировании дискретной цепи требования к цепи задаются в виде требований импульсной характеристики цепи или передаточной функции.
Обычно схему цепи строят по известной передаточной функции. Если схема цепи известна, то импульсную характеристику можно получить одним из следующих способов:
1) непосредственно по схеме, как реакцию цепи на δ–функцию;
2) решением разностного уравнения, полагая: x(nT)= δ(nT), y(nT)=H(nT);
3) по известной передаточной функции H(Z):
a) применяя обратное Z–преобразование,
b) применяя теоремы разложения для H(Z) (аналогично определению оригинала по известному изображению),
c) делением числителя H(Z) на знаменатель с последующим применением теорем линейности и запаздывания (простой способ).
Пример простого способа: Определить h(nT), если 


Применяя теорему линейности и запаздывания, получаем h(nT).
h(nT) = {0; 0.4; -0.032; 0.00256; …}
§13 Расчет сигнала на выходе цепи применением свертки.
Линейная свертка.
Спектр сигнала на выходе цепи равен произведению входного сигнала на передаточную функцию, т.е.
Y(jω) = X(jω) · H(jω)
В равной мере это относится и к Z–изображениям:
Y(Z) = X(Z) · H(Z)
Но произведению Z–изображений соответствует свертка сигнала:
 – формула линейной свертки.
– формула линейной свертки.
Пример: h(nT) = {1.0; 0.5}
Определить y(nT), если x(nT) = {0.8; 1.0}. Верхний предел можно взять n.

n=0; y(0T) = x(0T)·h(0T) = 0.8·1.0 = 0.8
n=1; y(1T) = x(0T) ·h(1T) + x(1T) ·h(0T) = 0.8·0.5 + 1.0·1.0 = 1.4
n=2; y(2T) = x(0T) ·h(2T) + x(1T) ·h(1T) + x(2T) ·h(0T) =
= 0.8·0 + 1·0.5 + 0·1 = 0.5![]()
Ответ: y(nT) = {0.8; 1.4; 0.5}
Круговая свертка.
Спектр периодического сигнала является дискретным, поэтому спектр на выходе периодического сигнала определяется произведением дискретных спектров.
Y(jkω1) = X(jkω1) · H(jkω1)
Это выражение имеет смысл лишь в том случае, когда периоды всех сигналов (y(nT), x(nT), h(nT)) одинаковы и следовательно число частотных отсчетов будет одинаковым для всех сигналов.
Если периоды сигналов будут разными, то все периоды выравниваются по максимальному периоду, а недостающие отсчеты заменяются нулями.
NT– число отсчетов в периоде, где больше период сигнала.
Произведению дискретных спектров соответствует свертка периодических сигналов на интервале равным одному периоду.
 – формула круговой свертки.
– формула круговой свертки.
Сигнал на выходе цепи имеет наибольшее количество отсчетов по сравнению с x(nT) и h(nT), т.е.
если N1 – число отсчетов x(nT)
N2 – число отсчетов h(nT),
то N = N1 + N2 – 1 – число отсчетов y(nT).
Пример: Исходные данные из предыдущего примера.
x(nT) = {0.8; 1.0} h(nT) = {1.0; 0.5}
N1 = 2 ; N2 = 2 ; N = 2 +2 – 1 = 3
X(nT) = {0.8; 1.0; 0} h(nT) = {1.0; 0.5; 0}


n = 0; y(0T) = x(0T)·h(0T) + x(1T) ·h(-1T) + x(2T) ·h(-2T) =
= 0.8·1 + 1·0 + 0·0.5 = 0.8
n = 1; y(1T) = x(0T)·h(1T) + x(1T) ·h(0T) + x(2T) ·h(-T) =
= 0.8·0.5 + 1·1 + 0·0 = 1.4
n = 2; y(2T) = x(0T)·h(2T) + x(1T) ·h(1T) + x(2T) ·h(0T) =
= 0.8·0 + 1·0.5 + 0·1 = 0.5
y(nT) = {0.8; 1.4; 0.5}

Реальные сигналы, поступающие на вход цепи для обработки, могут иметь большую протяженность, поэтому эти сигналы приходится секционировать, т.е. разбивать на секции.
![]()
![]()
xi(nT) – секция входного сигнала.
Секцию можно представить как дискретную периодическую последовательность и использовать круговую развертку.
 – секция выходного сигнала.
– секция выходного сигнала.
![]() – выходной сигнал.
– выходной сигнал.
На практике получили распределение два метода по секционной обработке.
1. Метод перекрытия с суммированием.
Входной сигнал разбивается на секции длиной L.
N1 = L – длина секции xi(nT)
N2 – длина h(nT)
N = N1 + N2 –1 – длина секции yi(nT)
Длина секции выходного сигнала больше длины секции входного сигнала на (N2 –1) отсчетов. Смежные секции выходного сигнала перекрываются на интервале (N2 –1). На этом интервале необходимо производить суммирование отсчетов.
2. Метод перекрытия с накоплением.
Входной сигнал разбивается на секции длиной L. Каждая секция наращивается слева (N2 –1) – отсчетами от предыдущей секции, в результате:
N1 = L +(N2 –1) – длина удлиненной секции xi(nT)
N2 – длина h(nT)
N = N1 + N2 –1 = L + 2(N2 –1) – длина секции yi(nT)
В результате искусственного удлинения входной секции, (N2 –1) отсчетов слева и (N2 –1) отсчетов справа выходной секции являются ложными и поэтому отбрасываются. Оставшиеся L отсчетов являются истинными и поступают на выход (они не перекрываются).
Дополнительной арифметической операции не требуется т.к. секции перекрываются.
Посекционная обработка применяется в том случае, когда дискретная система реализована в виде программы на ЭВМ. Если дискретная цепь состоит из реализованных отдельных элементов (умножителей, сумматоров, элементов памяти, т.е. в виде цепи), то необходимости посекционной обработки нет.
§15 Энергия дискретного сигнала.
В качестве энергии Wx дискретного сигнала x(nT) применяется мера:

Энергию можно вычислить и в частотной области, применяя равенство Парсеваля:

![]() – спектр сигнала x(nT).
– спектр сигнала x(nT).
![]() – спектр инверсного сигнала x(-nT).
– спектр инверсного сигнала x(-nT).
X(jω) · X*(jω) = X2(ω) = Sx(jω) – энергетический спектр сигнала x(nT).

Энергетическому спектру Sx(jω) соответствует во временной области корреляционная функция Sx(nT) сигнала x(nT).
В соответствии с определением энергетического спектра корреляционная функция определяется сверткой сигнала с инверсной копией.
 – формула корреляции сигнала x(nT).
– формула корреляции сигнала x(nT).
Согласно формуле корреляции в точке:
n = 0 
Если Sx(jω) – спектр непрерывного сигнала Sx(nT), то Sx(jmω1) – спектр периодической дискретной последовательности Sx(nT).
Периодическая дискретная последовательность Sx(nT) определяется через свой спектр по формуле обратного ДПФ.

При n = 0 
 – равенство Парсеваля для периодической
дискретной последовательности.
– равенство Парсеваля для периодической
дискретной последовательности.
§16 Расчет энергии сигнала дискретной цепи.
Расчет корреляционной функции на выходе цепи:
корреляционная функция выходного сигнала – Sy(nT), Sx(nT) и Sh(nT).

Где ![]() – условное обозначение свертки.
– условное обозначение свертки.
Докажем справедливость этой формулы:
![]()
![]() т.к. система линейная и математические
операции линейные, то сигнал можно сочетать различными способами
т.к. система линейная и математические
операции линейные, то сигнал можно сочетать различными способами ![]()
Согласно полученному выражению энергию полученного сигнала можно получить без расчета выходного сигнала.
n = 0 ![]()
Рассмотрим важный частный случай: пусть x(nT) – случайный сигнал с нулевым средним. Для такого сигнала:
Sx(nT) = Sx(0T) = Wx = σx2 – дисперсия сигнала x(nT)
Тогда ![]()
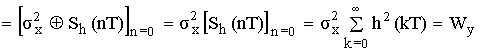
– формула расчета выходного сигнала (применяется для расчета шумов квантования в цифровых фильтрах).
Пример: определить энергию сигнала на выходе цепи с импульсной характеристикой.
h(nT) = {1.0; 0.5} и x(nT) = {0.5; 0.5}
a) расчет энергии Wy во временной области.
Определяем y(nT) с помощью круговой свертки.
N1 = 2; N2 = 2; N = N1 + N2 –1 = 3

h(nT) = {1; 0.5; 0} ![]() x(nT) = {0.5; 0.5; 0}
x(nT) = {0.5; 0.5; 0}

n = 0 y(0T) = x(0T)·h(0T) + x(1T) ·h(-1T) + x(2T) ·h(-2T) =
= 0.5·1 + 0.5·0 + 0·0 = 0.5
n = 1 y(1T) = x(0T) ·h(1T) + x(1T) ·h(0T) + x(2T) ·h(-1T) = 0.75
n = 2 y(2T) = x(0T) ·h(2T) + x(1T) ·h(1T) + x(2T) ·h(0T) = 0.25

b) расчет энергии Wy в частотной области.
С помощью равенства Парсеваля определяем частотные отсчеты выходного сигнала по формуле прямого ДПФ.

m = 0 Y(j0ω1) = y(0T) + y(1T) + y(2T) = 1.5
m = 1 Y(j1ω1) = y(0T)ej 0 + y(1T)e–j 120 + y(2T)e–j 240 = –j0.435
m = 2 Y(j2ω1) = y(0T)ej 0 + y(1T)e–j 240 + y(2T)e–j 480 = j0.435
Y(j0ω1) = {1.5; –j0.435; j0.435}
 с) расчет энергии сигнала Wy
по корреляционным функциям Sx(nT) и Sh(nT).
с) расчет энергии сигнала Wy
по корреляционным функциям Sx(nT) и Sh(nT).
![]()
x(nT) = {0.5; 0.5}; h(nT) = {1.0; 0.5}

N1 = 2; N2 = 2; N = N2 + N1 – 1 = 3
x(nT) = {0.5; 0.5; 0}

n = 0; Sx(0T) = x(0T)·x(0T) + x(1T) ·x(1T) + x(2T) ·x(2T) =
= 0.5·0.5 + 0.5·0.5 + 0·0 = 0.5
n = 1; Sx(1T) = x(0T)·x(1T) + x(1T) ·x(2T) + x(2T) ·x(3T) = 0.25
n = 2; Sx(2T) = x(0T)·x(2T) + x(1T) ·x(3T) + x(2T) ·x(4T) = 0.25
Sx(nT) = {0.5; 0.25; 0.25}
Sh(nT) = {1.25; 0.5; 0.5}
N1 = 3; N2 = 3; N = N1 + N2 – 1 = 5
Периоды корреляционных функций, участвующих в свертке, нужно увеличить таким образом, чтобы четный характер корреляционной функции сохранился.
Исходная периодическая последовательность для Sx(nT) (период =3)

Последовательность после увеличения периода (период = 5):

В результате выравнивания периода получаем:
Sx(nT) = {0.5; 0.25; 0; 0; 0.25}
Sh(nT) = {1.25; 0.5; 0; 0; 0.5}

n = 0; Sy(0T) = Wy = Sx(0T)·Sh(0T) + Sx(1T)·Sh(-1T) + Sx(2T)·Sh(-2T) +
+ Sx(3T)·Sh(-3T) + Sx(4T)·Sh(-4T) = 0.5·1.25 + 0.25·0.5 + 0·0 + 0·0 + 0.25·0.5 =
= 0.625 + 0.125 + 0.125 = 0.875
Wy = 0.875
Цифровая система для обработки сигнала.
Цифровая форма реализации дискретной цепи называется цифровым фильтром.
В цифровом фильтре в отличие от дискретной цепи действия над отсчетами заменяются соответствующими цифрами, которые представлены в виде кодовых слов (нули, единицы).
Структура цифровой системы для обработки сигнала.

ЭК – электронный ключ
АЦП – аналого-цифровой преобразователь
ЦФ – цифровой фильтр
ЦАП – цифро-аналоговый преобразователь
СФ – синтезирующий фильтр (ФНЧ)
Цифровая схема как и дискретная схема описывается теми же уравнениями. Отличие цифровой структуры состоит в том, что сигнал на выходе отличается от идеального варианта на величину уровня шумов квантования.
Применение вычислительной техники позволяет получить высокое качество обработки сигнала, несмотря на наличие шумов квантования. Шумы квантования можно минимизировать не только увеличением длины кодовых слов, но и путем рационального конструирования цифровой схемы.
Расчет рекурсивных и не рекурсивных цифровых фильтров имеет свои особенности, поэтому расчеты этих фильтров будем рассматривать отдельно.
§18 Расчет не рекурсивного ЦФ общего вида.
Каноническая схема:

N – число отводов фильтра
Различают расчет не рекурсивного ЦФ во временной области (по импульсной характеристике), и в частотной области (по частотной характеристике).
а) Расчет фильтра во временной области.
Требуемая импульсная характеристика имеет как правило бесконечную протяженность, поэтому приходится ограничивать импульсную характеристику первыми N отсчетами.
Отбрасываемые отсчеты определяют погрешность, которую можно оценить по среднеквадратическому критерию близости.
h(nT) = {a0; a1; a2; …aN-1}
Коэффициенты проектируемого фильтра принимаются равными соответствующим отсчетам импульсной характеристики.
В заключении расчета фильтра выполняются расчеты шумов квантования, погрешностей оптимального динамического диапазона.
б) Расчет фильтра в частотной области.
В начале расчета требуемые частотные характеристики надо продолжить на диапазон [0.5ωg; ωg] по принципу комплексно-сопряженной симметрии.

Надо задаться значением N и определить отсчеты частотной характеристики.
![]()
![]()
После выполнения всех расчетов значение N уточняется.
Определить расчеты h(nT) можно по формуле:

Таким образом, значение коэффициентов фильтров становится известным, после этого находим выражение для передаточной функции фильтра H(Z) и выполним проверку.

В отсчетные моменты реализуемые и требуемые характеристики совпадают, а между отсчетами не совпадают. Отличие тем меньше, чем больше N.
Не рекурсивные фильтры позволяют получить четную или нечетную импульсную характеристику и как результат – линейную фазу, потому что у четных и нечетных сигналов спектр фаз строго линейный.
Рассмотрим различные варианты фильтров с линейной фазой.
1. Симметричные фильтры.
а) N – нечетное (N=5 отводы)


H(Z)
= a2 + a1Z–1 + a0Z–2
+ a1Z–3 + a2Z–4 = Z–2
[a0 + a1(Z + Z–1) + a2(Z–2
+ Z2)]
Z = ejωT АЧХ – функция четная относительно 0.5ωg (т.к. cos – четн.). б) N – четное (N = 4)
![]()
![]()
![]()
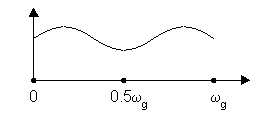
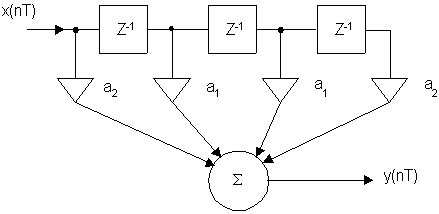

H(Z) = a2 + a1Z–1
+ a1Z–2 + a2Z–3 = Z–1. 5
[a1(Z0. 5 + Z–0. 5) + a2(Z1.
5 + Z-1. 5)] Z = ejωT φ(ω)
= -1.5ωТ функция четная, т.к: cos0.5ωT + cos1.5ωT
– функция нечетная. 2.Антисимметричные
фильтры. а) N – нечетное (N
= 5)![]()
![]()



H(Z) = a2 + a1Z–1
+ a0Z–2 – a1Z–3 – a2Z–4
= Z–2 [a1(Z–1 – Z–1) + a2(Z2
– Z–2)]
Z = ejωT

![]()
![]()


Функция нечетная.
б) N – четное (N= 4)


H(Z) = a2 + a1Z–1
– a1Z–2 – a2Z–3 = Z–1. 5
[a1(Z0. 5 – Z–0. 5) + a2(Z1.
5 – Z-1. 5)]
Z = ejωT
![]()
![]()
![]()

Функцияφ(ω) четная, т.к. sin0.5ωT и sin1.5ωT – четные.
§20 Общие свойства фильтра с линейной фазой.
Анализ различных вариантов фильтров с линейной фазой позволяет выделить ряд общих свойств:
1. для симметричных фильтров
![]()
H(ω) – четн., если N
нечет. ![]()
H(ω) – нечетн., если
N четн. ![]()
2. для антисимметричных фильтров
![]()
H(ω) – четн., если N
четн. ![]()
H(ω) – нечетн., если
N нечетн. ![]()
На основании общих свойств можно сформулировать рекомендации при проектировании фильтров с линейной фазой.
1. Если ![]() , то фильтр симметричный;
, то фильтр симметричный;
Если ![]() , то фильтр антисимметричный;
, то фильтр антисимметричный;
2. Если ![]() , то АЧХ – четная, т.е. N
– нечетн. для симметричных фильтров и N – четн. для антисимметричн. фильтров.
, то АЧХ – четная, т.е. N
– нечетн. для симметричных фильтров и N – четн. для антисимметричн. фильтров.
Если ![]() , то АЧХ – нечетная, т.е. N
– четн. для симметричных фильтров и N – нечетн. для антисимметричн. фильтров.
, то АЧХ – нечетная, т.е. N
– четн. для симметричных фильтров и N – нечетн. для антисимметричн. фильтров.
3. Учитывая свойства фильтров с линейной фазой, АЧХ нужно продолжить на диапазон [0.5ωg; ωg] следующим образом:

4. Антисимметричные фильтры применяются чаще в тех случаях, когда требуемая передаточная функция содержит мнимую единицу j (дифференциатор) в качестве множителя.
H(jω) = jω
H(ω) = ω
§21 Расчет фильтров с линейной фазой.
Расчет осуществляется по общим правилам расчета нерекурсивных фильтров, но нужно учитывать общие свойства фильтров с линейной фазой.
Пример: Рассчитать ФНЧ с линейной фазой.
ПП = [0; 200] Гц
Переходные области [200; 300] Гц
Решение:
Выбираем fg
= 800 Гц ;  ; ПП [0; 0.25] ;
; ПП [0; 0.25] ;
переходная область [0.25; 0.375]
Пусть N = 8

Фильтр симметричный, т.к. H(0) = 1
 отсчеты АЧХ
отсчеты АЧХ
 отсчеты ФЧХ
отсчеты ФЧХ
![]()


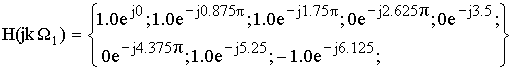
Применим формулу обратного ДПФ.
 = {0.065; -0.165; -0.025;
0.53; 0.53; 0.025;
= {0.065; -0.165; -0.025;
0.53; 0.53; 0.025;
-0.165; 0.065}

![]()
H(Z) = 0.065 – 0.165Z–1 + 0.025Z–2 +0.53Z–3 + 0.53Z–4 +0.025Z–5 –
– 0.165Z–6 – 0.065Z–7
H(Z) = Z–3. 5 [0.53(Z0. 5 + Z–0. 5) + 0.025(Z1. 5 + Z–1. 5) – 0.165(Z2. 5 + Z–2. 5) +
+ 0.065(Z3. 5 + Z–3. 5)]
H(jΩ) = e–7 πΩ(1.06cosπΩ + 0.05cos3πΩ – 0.33cos5πΩ + 0.13cos7πΩ)
![]()
Чтобы улучшить аппроксимацию требуемой характеристики АЧХ вблизи точек разрыва применяют весовую функцию (W(nT)) – сглаживающее окно.
В качестве примера рассмотрим окно Хеминга W(nT).

Применим окно Хеминга в нашем примере:
![]()
Рассчитываем отсчеты окна:
W(nT) = {0.08; 0.244; 0.64; 0.96; 0.96; 0.64; 0.244; 0.08}
![]() (nT) = {0.005;
–0.04; 0.016; 0.51; 0.51; 0.016; –0.04; 0.005}
(nT) = {0.005;
–0.04; 0.016; 0.51; 0.51; 0.016; –0.04; 0.005}

![]() = 0.005 – 0.04Z–1 + 0.016Z–2
+ 0.51Z–3 + 0.51Z–4 + 0.016Z–5 –
= 0.005 – 0.04Z–1 + 0.016Z–2
+ 0.51Z–3 + 0.51Z–4 + 0.016Z–5 –
– 0.04Z–6 + 0.005Z–7
Отсюда получаем выражение АЧХ и строим график:
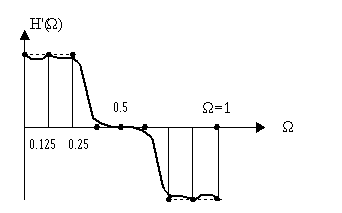
Получили меньше отклонений, применив сглаживающее окно. Эффект “сглаживающее окно” особенно эффективно для больших значений N.
Метод расчета с применением весовой функции получил название: метод взвешивания.
назад | оглавление | вперёд
