| Цифровая обработка сигналов |
| Часть2 §22 Метод частотной выборки. |
назад | оглавление | вперёд |
Схема фильтра по методу частотной выборки строится с таким расчетом, чтобы коэффициенты фильтра соответствовали частотным отсчетам частотной характеристики.
а) Схема фильтра получается путем эквивалентных преобразований передаточной функции нерекурсивного фильтра.
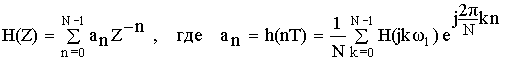

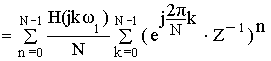
Применим : 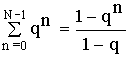
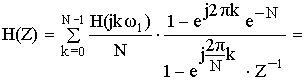
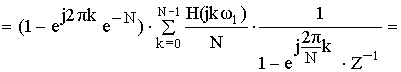
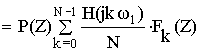
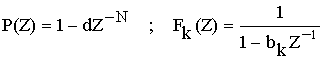

В соответствии с полученным результатом схема нерекурсивного фильтра примет следующий вид:

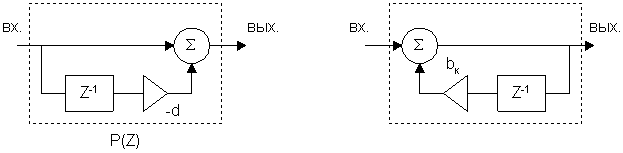
![]()
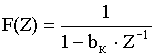
Нули и полюсы полученной передаточной функции 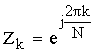 совпадают и расположены на единичной окружности
плоскости Z. Чтобы исключить возможность самовозбуждения,
нули и полюсы целесообразно сместить внутрь единичной окружности на малую
величину.
совпадают и расположены на единичной окружности
плоскости Z. Чтобы исключить возможность самовозбуждения,
нули и полюсы целесообразно сместить внутрь единичной окружности на малую
величину.
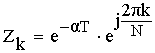 – новое положение нуля и полюса.
– новое положение нуля и полюса.
![]()
Требуемое смещение нулей и полюсов функции получаем за счет некоторого изменения коэффициентов dи bK.

b) Частотная характеристика фильтра.
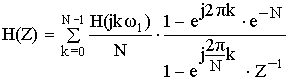
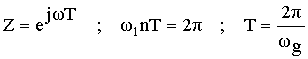
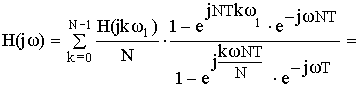
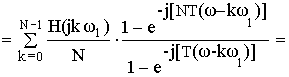

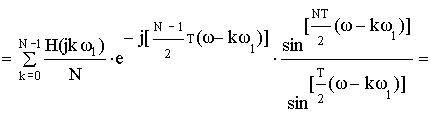
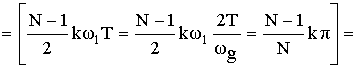

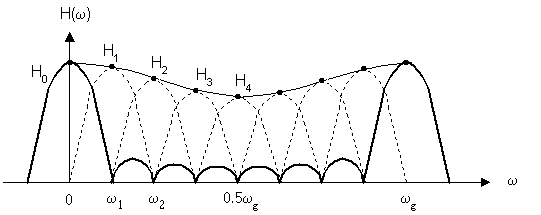
Частотная характеристика фильтра по методу частотной выборки получилась в форме ряда Котельникова для спектров дискретных сигналов, т.е. частотная характеристика состоит из суммы отсчетных функций, причем регулировка амплитуды каждой из отсчетнной функции не влияет на амплитуду других отсчетных функций.
Рассмотрим формирование суммы отсчетных функции на примере некоторой АЧХ.

в) Схема фильтра с вещественными отводами.
Передаточная функция отводов kи N-kявляется комплексно-сопряженной, потому что частотная характеристика удовлетворяет условию комплексно-сопряженной симметрии.
Объединяя отводы kи N-k, мы получим один отвод с вещественными коэффициентами.
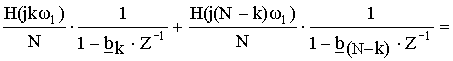


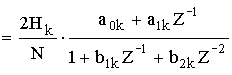

Полученному выражению соответствует схема:

Схема с вещественными отво-дами получила преимущественное распространение. Важное досто-инство: в схеме фильтра отсут-ствуют комплексные отводы соответствующие нулевым зна-чениям требуемой частотной характеристики.
§23 Расчет рекурсивных фильтров.
При расчете рекурсивных фильтров применяются прямые и косвенные методы.
Косвенные методы предполагают в качестве промежуточного этапа расчет аналогового фильтра (АФ). Затем по передаточной функции АФ получают схему цифрового фильтра (ЦФ).
Метод билинейного преобразования.
Основой этого метода является такое преобразование частоты, при котором частотная характеристика АФ сжимается до конечных размеров. В результате ошибок наложения, которые всегда существуют при переходе от АФ к ЦФ, частотные преобразования осуществляются с помощью выражения:
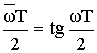 где
где ![]()
ω – реальная частота (частота ЦФ). Тогда:
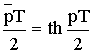
Соотношение между реальной и расчетной частотой удобно изобразить на графике.
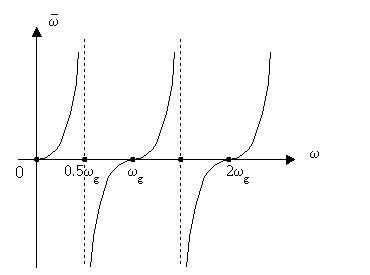
Рассмотрим графически, как преобразуется частотная характеристика АФ в частотную характеристику ЦФ.
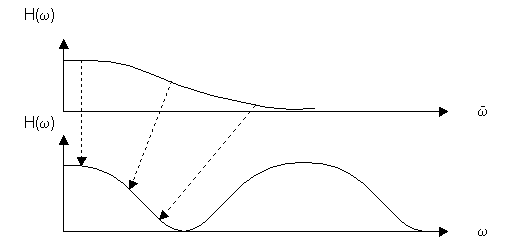
Рассмотрим соотношение частот pи
![]() по отношению к Z-плоскости.
по отношению к Z-плоскости.
Соотношение между P и Z:
![]()
Соотношение между ![]() и Z-плоскостью:
и Z-плоскостью:
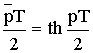 , тогда
, тогда 
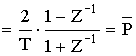
Последовательность расчета по методу билинейного преобразования.
1) Задано: норма на АФ
переходит на ЦФ. 
2) Рассчитать АФ в соответствии
с полученными нормами. В результате расчетов становится известной передаточная
характеристика H(![]() ).
).
3) Определить H(Z)
по H(![]() ) применяя формулу:
) применяя формулу: 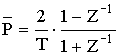
4) По передаточной функции H(Z) построить схему ЦФ.
5) Выполнить нужные расчеты по учету эффекта конечных разрядностей.
Недостаток метода в том, что преобразование частот носит нелинейный характер. Метод применяется, в основном, при проектировании частотно–селективных фильтров.
Пример:
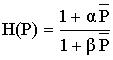
Решение: определим H(Z) подстановкой

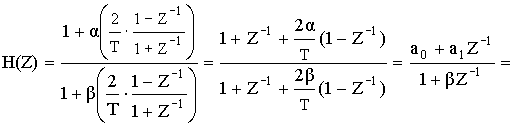
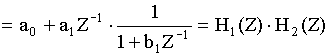
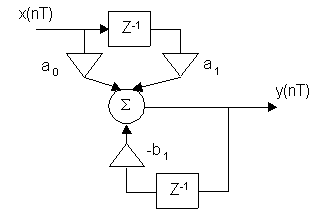
§24 Эффекты конечной разрядности и их учет.
Шумы квантования и шумовая модель.
Отсчеты сигнала в АЦП округляются к ближайшему разрешенному уровню. Расстояние между смежными уровнями квантования равно шагу квантования Δ. В результате кодовые слова имеют конечную разрядность после округления (b – разрядность кодовых слов). Значение младшего разряда кодового слова равно шагу квантования.
Δ и b связаны соотношением:
Δ = 2 -b
Разность между истинным отсчетом и квантованным результатом:
e(nT) = e(n) – ошибка квантования.
Ошибка квантования определяется неравенством:
![]() при округлении результата.
при округлении результата.
![]() при усечении результата.
при усечении результата.

Квантование происходит не только в АЦП, но и в умножителе т.к. при умножении кодовых слов разрядность результата равна сумме разрядностей множимого и множителя.
Ошибки округления на выходе цифрового фильтра воспринимаются в виде шума, который называется шумом квантования.
Расчет шумов квантования на выходе ЦФ осуществляется по шумовой модели, которая отличается от исходной цепи наличием источников шума.
Пример:

e0(n) – шум от АЦП
ei(n) – шум от умножителя

Расчет шумов квантования.
Оценку шума можно выполнить по максимуму шума или усредненной энергии шума:
1. первая оценка соответствует наихудшему случаю,
2. вторая оценка соответствует условию вероятностного подхода к решению задачи.
Расчет максимального шума.
Шум на выходе цепи eiвых(n) определяют по формуле свертки:
![]()
где: ei(k) – шум на выходе i-го источника шума;
hi (n) – импульсная характеристика участка цепи от выхода i-го источника шума до выхода цепи.
Maксимум шума на выходе цепи ei вых max (n) = Eiвозникает в случаях:
1. когда ei (k) и hi (n-k) имеют одинаковые знаки;
2. когда на выходе i-го источника наблюдается max шума.
![]() при округлении
при округлении
eimax(n) = Δiпри усечении
Тогда max шума на выходе цепи:
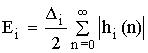 при округлении.
при округлении.
Maxшума на выходе цепи от всех источников при условии наихудшего случая будет наблюдаться тогда, когда maxшума на выходе цепи от всех источников будут складываться.
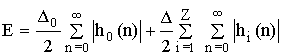
![]() – maxшума на выходе АЦП,
– maxшума на выходе АЦП,
![]() – maxшума на выходе каждого из Z умножителей,
если разрядность всех умножителей одинакова.
– maxшума на выходе каждого из Z умножителей,
если разрядность всех умножителей одинакова.
Расчет уровня шума по условию наихудшего случая приводит к тому, что уровень реального шума значит меньше расчетного. Чаще применяется расчет усредненного значения.
§25 Расчет усредненной энергии шума.
Расчет усредненной энергии шума на выходе цепи от i-го источника шума выполняется по формуле:
![]()
где: σi2 – дисперсия шума на выходе i-го источника шума;
hi (n) – импульсная характеристика.
Шум квантования представляет собой случайную последовательность типа “белый” шум, поэтому σi2 на выходе i-го источника определяется:
 при округлении чисел;
при округлении чисел;
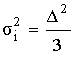 при усреднении чисел.
при усреднении чисел.
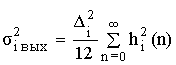
Источники шума не коррелированны между собой, поэтому усредненная энергия шума на выходе цепи от всех источников получается сложением усредненной энергии шума от каждого источника.
Усредненная энергия шума от всех источников на выходе цепи определяется по формуле:

где: ![]() – усредненная энергия шума на выходе
АЦП;
– усредненная энергия шума на выходе
АЦП;
М – число ветвей цифрового фильтра;
![]() – усредненная энергия шума на выходе
каждого из Z-умножителей, если разрядность всех умножителей
одинакова.
– усредненная энергия шума на выходе
каждого из Z-умножителей, если разрядность всех умножителей
одинакова.
Расчет уровня шума по условию вероятностной оценки вполне удовлетворительно соответствует реальному уровню шума, но в этом случае не исключены кратковременные скачки уровня реального шума по отношению к расчетному.
§27 Влияние структуры цепи на шум квантования.
Если в передаточной функции некоторой цепи имеются высокодобротные полюсы, то отсчеты импульсной характеристики этой цепи медленно убывают с ростом номера отсчета, поэтому шум квантования оказывается значительным. Уровень шума такой цепи можно понизить, применяя каскадную реализацию цепи.
Каскадная реализация цепи начинается с синтеза передаточной функции в виде произведения простейших сомножителей.

где: Z0m – нули H(Z);
Z∞m – полюсы H(Z).
Нули и полюсы группируются в пары по принципу: каждому полюсу подбирается ближайший расположенный к нему ноль.
Сомножителям первого порядка (нули, полюсы вещественные) соответствуют звенья первого порядка. Сомножителям второго порядка (нули, полюсы комплексно-сопряженные) соответствуют звенья второго порядка.
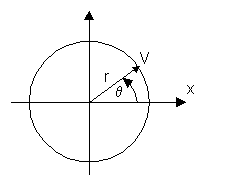
Звенья располагаются в порядке возрастания добротности. Добротность комплексных полюсов для плоскости Z определяется:
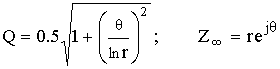
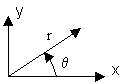
![]() – угол (частота) полюса;
– угол (частота) полюса;
r – радиус полюса.
В качестве формулы добротности воспользуемся анализом:
Q = r
Пример: осуществить каскадную реализацию передаточной функции.
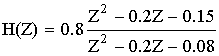
Z2 – 0.2Z – 0.15 = 0
![]()
Z2 – 0.2Z – 0.08 = 0
![]()
![]()


§28 Квантование коэффициентов.
Специализированный процессор, предназначенный для обработки сигналов, будет тем эффективней (экономически), чем короче кодовые слова. Кодовые слова коэффициентов имеют конечную разрядность, т.к. при переходе от расчетных значений к двоичному представлению коэффициента кодовые слова получаются бесконечной разрядности, поэтому бесконечную разрядность приходится ограничивать.
Чем меньше разрядность коэффициента, тем больше погрешность синтезируемых характеристик. Поэтому квантовать коэффициенты надо с таким расчетом, чтобы не превысить допуск на отклонение синтезируемых характеристик.
При переходе к двоичному числу целая часть числа будет изображать знак, причем: “1” будет стоять в целой части, если знак “–”,
“0” будет стоять в целой части, если знак “+”.
Дробная часть числа характеризует модуль числа.
Пример:
Дано десятичное число с фиксированной запятой.
A(10) = 0.32 определить A(2) = ?
A(2) = 0010100011 Разрядность 8 кодовых слов
| -0.32 |
0.64 |
1.28 |
0.56 |
1.12 |
0.24 |
0.48 |
0.96 |
1.92 |
1.84 |
A(2) = 0.010100100 => A(2) = 0.01010010 при округлении
A(2) = 0.010100011 => A(2) = 0.01010001 при усреднении
Для оценки погрешности выполним обратный переход к A(10)
При округлении A(10) @ 0·2 – 1 + 1·2 – 2 + 0·2 – 3 + 1·2 – 4 + 0·2 – 5 + 0·2 – 6 +
+ 1·2 – 7 + 0·2 – 8 = 0.3203125
Δ – абсолютная погрешность
Δ = 0.3203125 – 0.32 = 0.0003125
![]() –относительная погрешность.
–относительная погрешность.
При усечении A(10) @ 0.31640625
Δ = 0.32 – 0.31640625 = 0.00359375
![]()
Для расчета разрядности существуют различные методы, самый простой – метод проб.
Последовательность расчета по методу проб.
1. задаться разрядностью коэффициента ориентировочно (8,10);
2. рассчитать новые значения коэффициентов для выбранной разрядности;
3. рассчитать системные характеристики цепи с новыми коэффициентами цепи;
4. оценить погрешность системных характеристик;
5. изменить разрядность коэффициентов в ту или иную сторону, в зависимости от погрешности системных характеристик и повторить расчет.
§29 Масштабирование сигнала в цепи.
Шум квантования на выходе цифровой цепи не зависит от уровня сигнала. Чем выше уровень сигнала в цепи, тем лучше соотношение сигнал/шум. Но высокие уровни сигнала могут привести к переполнению (перегрузке) сумматора, т.е. к выходу числа за пределы разрядной сетки слева.

Чтобы получить нужный уровень применяется масшта-бирование сигнала. С этой целью на входе цепи уста-навливают умножитель с коэффициентом умножения λ.
Для расчета λ используют различные методы.
1. Расчет λ по условию ограничения максимума сигнала.
Сигнал на выходе i-го сумматора, т.е. yi (n) можно рассчитать применением свертки:
![]()
Условия maxсигнала yi(n)

Учитывая эти условия получим формулу для максимально возможного сигнала на выходе сумматора.
![]()
Потребуем, чтобы maxyi(n) = 1
![]()

Расчет λ выполняется по каждому сумматору. Из всех λ выбирается наименьшее и округляется в меньшую сторону до ближайшего числа кратного степени 2, что позволяет осуществить умножение простым сдвигом числа в числовом регистре.
Расчет λ по условию max сигнала приводит к низким уровням сигнала цепи, поэтому расчет λ часто выполняется по условию ограничения энергии сигнала.
2. Расчет λ по условию ограничения энергии сигнала.
Расчет энергии сигнала на выходе i-го сумматора определяется:
![]() формула справедлива для случайного
сигнала с равномерным энергетическим спектром, что соответствует реальному
сигналу.
формула справедлива для случайного
сигнала с равномерным энергетическим спектром, что соответствует реальному
сигналу.
![]()
Энергия сигнала на выходе i-го сумматора равна энергии сигнала на входе, т.е. Wyi = Wx. В результате исходная формула примет вид:
![]()
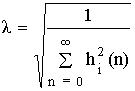
Уровень сигнала цепи получается выше, но здесь не исключена возможность перегрузки сумматора (но вероятность перегрузки мала).
3. Расчет λ по условию ограничения максимума усиления цепи.
Спектр сигнала на выходе i-го сумматора определяется:
![]()
Если ω∞ – частота максимального усиления сигнала, то условие максимума усиления сигнала запишется:
![]()
где: ω∞ – частота высокодобротного полюса
![]() – коэффициенты высокодобротного полюса.
– коэффициенты высокодобротного полюса.
Потребуем, чтобы Y(ω∞) = X(ω∞), тогда выражение для максимального спектра выходного сигнала принимает вид:
1 = λ H(ω∞)
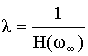
Расчет λ приводит к значениям λ, где–то между случаями 1 и 2. Расчет λ в этом случае применяется для каскадной реализации, когда масштабирование осуществляется внутри каждого звена, за счет чего масштабирование получается очень эффективным.
§30 Оценка эффективности использования
динамического диапазона цепи.
Масштабирование позволяет повысить эффективность использования динамического диапазона. Динамический диапазон цепи определяется границами выходного сигнала [Δ; 1.0] применительно к числам фиксированной запятой.
Δ – значение младшего разряда кодового слова.
Эффективность использования динамического диапазона определяется с одной стороны значением вероятности перегрузки сумматоров, и помехозащищенностью Rш сигнала с другой стороны.
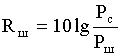
Pc – мощность сигнала на выходе цепи
Pш – мощность шума на выходе цепи
Рассчитать Rш можно и по-другому, учитывая равенство:
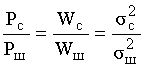
Предельными циклами называют ложные сигналы, которые возникают на выходе цепи, если на вход поступает сигнал в виде константы.
Предельные циклы появляются на выходе цепи вследствии ограничения разрядности кодовых слов на выходе умножителей.
Пример:
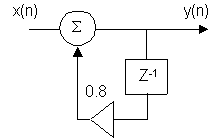
Определить форму и величину предельных циклов, если в последовательности x(n) в момент времени t=0 наступила пауза. При этом Y(–1) = 0.5, учитываем, что значение сигнала на выходе цепи ограничивается десятыми долями.
y(n) = x(n) + 0.8y(n – 1)
n=0 y(0) = 0 + 0.8·0.5 = 0.4
n=1 y(1) = 0 + 0.8·0.4 = 0.32 @ 0.3
n=2 y(2) = 0 + 0.8·0.3 = 0.21 @ 0.2
n=3 y(3) = 0 + 0.8·0.2 = 0.16 @ 0.2
n=4 y(4) = 0 + 0.8·0.2 = 0.16 @ 0.2
y(n) = {0.4; 0.3; 0.2; 0.2; 0.2…}
Если коэффициент (0.8) заменить на (–0.8), то на выходе получим:
y(n) = {–0.4; –0.3; –0.2; –0.2; –0.2…}
Предельный цикл становится знакопеременным.
Для цепи высокого порядка предельные циклы имеют сложную форму, которые трудно поддаются теоретическому анализу. При проектировании цифровых фильтров величина и форма предельных циклов выявляется результатом моделированием на ЭВМ.
§32 Чувствительность цифровых фильтров.
Чувствительностью величины m по параметру q называют соотношение:

Чувствительность показывает на сколько процентов изменится величина m, если параметр q изменится на 1%.
Для цифровой цепи часто в качестве величины m берут частотную характеристику.
![]()

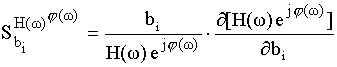
После дифференцирования получаем формулу чувствительности АЧХ и ФЧХ.
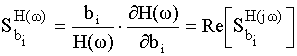 – чувствительность АЧХ
– чувствительность АЧХ
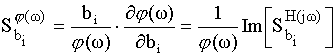 – чувствительность ФЧХ
– чувствительность ФЧХ
Пример:




Полученная частотная зависимость показывает на сколько процентов изменится АЧХ на каждой частоте, если коэффициент b изменился на 1%.
назад | оглавление | вперёд