Лекция 3

Теория сигналов

1)    Базовые модели сигналов

- описывание сигналов кок функция времени

Колебания могут быть дискретными и случайными

а) гармоническое колебание

б) функция Хевисайда

в) - функция Дирака

     -выражение - функции

Строб – короткий импульс.

Связь функции Хавасайда и - функции :

      Все 3 колебания являются пробными функциями и используются для представления сигнала (ряд Фурье)

Динамическое представление сигналов

1)  Представление - функуии

    - динамическое представление сигнала функцией Хавасайда

  -  общий случай

2)    Представление - функуии

 - функция S в момент времени

 - ширина прямоугольника

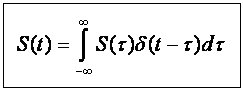
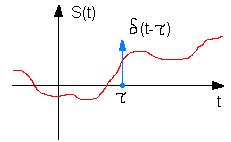
- Динамическое представление сигнала с помощью дельна функции

Пространство сигналов

1)    Аксиомы линейного пространства

Пусть есть некоторое множество М – векторов и на нём определена операция сложения . Множество относительно сложению должно быть замкнуто, т. е. :

Пример:

Нужно установить взаимнооднозначную связь между множества векторов и множества сигналов

A1.    ассоциативность:

А2.    существование нулевого элемента

А3.    существование обратного элемента:

А4.     коммутативность:

А1,А2,А3 – группа аксиом ,        А4 – абелева группа    

К – поле скаляров

Поле – множество, которое является коммутативным относительно чисел, а такие коммутационной группой относительно умножения (за исключением существования элемента обратным относительно умножению для нуля).

R – поле вещественных чисел

С – поле комплексных чисел

GF = {0;1}  - поле Галуа

Б1.  Ассоциативность умножения на скаляр

Б2.   Существование 0 и 1

Б3.  Существование единичного вектора

Б4.   Дистрибутивность

Все это есть векторное пространство

Пример: