Лекция №4

1)     - Система векторов

2)                                                                                                                                         

3)                                                                                                                                           

4) 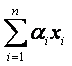                                                                                                                                         - линейная комбинация

5)                                                                                                                                           

6)                                                                                                                                         Линейная оболочка

7)                                                                                                                                          

8)                                                                                                                                          Совокупность векторов называется линейно независимыми если из

9)                                                                                                                                         
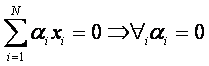
 Пример линейного пространства:

10)                                                                                                                                    

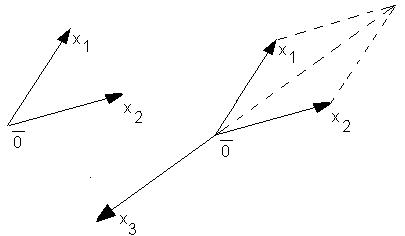
11)                                                                                                                                           Если совокупность векторов линейно независима, то её линейная оболочка образует n-мерное пространство.

12)                                                                                                                                           Базисом пространства называется совокупность векторов линейная оболочка которой совпадает с данным пространством.

13)                                                                                                                                      

14)                                                                                                                                           ПР.

15)                                                                                                                                           Дискретные сигналы:

16)                                                                                                                                      

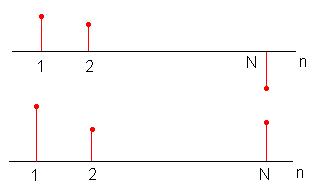
- вектор

Выбираем:

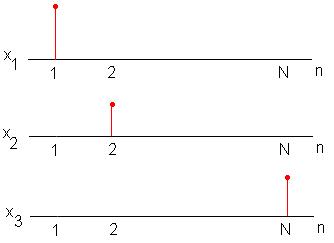
      Это пространство конечное, также может представить бесконечномерное:

      ПР.

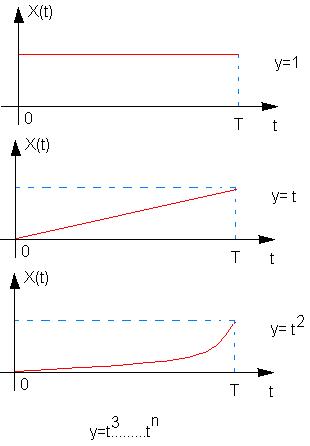
Структура пространственного сигнала

Метрика (R),

    Метрика – функционал

  Функционал – это отображение множества векторов в поле вещественных чисел R.

17)                                                                                                                                     - метрика

18)                                                                                                                                         Метрика определяет расстояние от x до y.

19)                                                                                                                                      

20)                                                                                                                                      

21)                                                                                                                                           Аксиомы (требования)

22)                                                                                                                                      

23)                                                                                                                                                                                                     

24)                                                                                                                                         Метрическое пространство              

25)                                                                                                                                                                                                      

   Пространство, в котором определена метрика, называется метрическим.

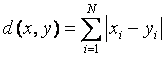
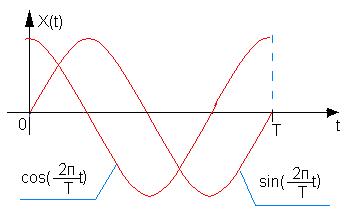
Наиболее популярной является: 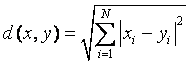 - Эвклидова метрика.

ПР.

Норма (R)

      Норма – это функционал отображающий множество векторов в поле вещественных чисел R.

     Аксиомы  (требования):

Нормированное пространство                 

Число определяющее метрику через норму:     .

Скалярное произведение (С) (x,y)

    Скалярное произведение – функционал, отображающий множество векторов на поле комплексных чисел С.

     Условия (требования)

Чаще всего :

        Если скалярное произведение определяет норму, а норма определяет метрику, то это унитарное пространство или предгильбертово.

ПР.

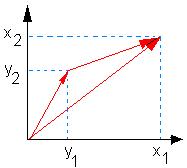
К n-мерному пространству дискретному сигналу:

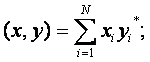
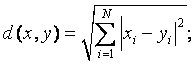
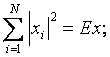
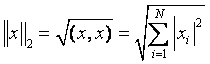                       - n-мерное эвклидово пространство

При - бесконечномерное эвклидово пространство.

Сигналы непрерывного времени (аналоговые сигналы).

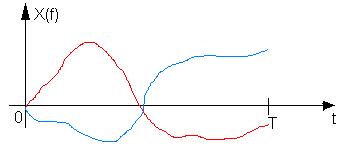
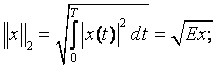
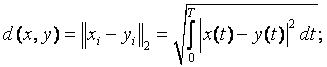
Таким образом, можно определить расстояние между 2я сигналами

   или    

Если (x,y)=0 – сигналы ортогаральны  

ПР.

 - неравенство Шварца.

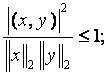
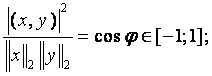
Упрощенная структурная схема приёмника ортогональными сигналами

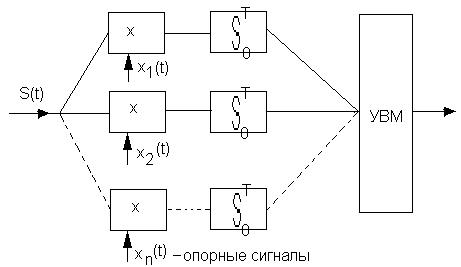
УВМ – устройство выбора максимума

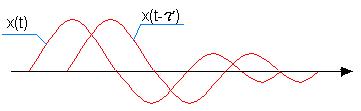
  - взаимно корреляционная функция детерминированных сигналов.

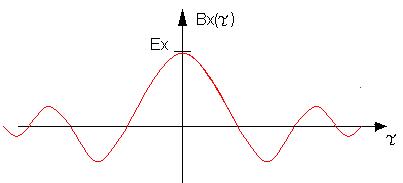
При

 - авто корреляционная функция детерминированных сигналов.

При

ПР.