10.2. Дифференциальные уравнения первого порядка – уравнение, разрешенное относительно производной. Теорема. О существовании и единственности решения (Теорема Ковалевской). Пусть непрерывна в открытой области Д и . Открытая область – это область без своей границы. 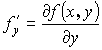– существует и непрерывна в Д, гладкая по . Пусть Тогда имеется решение такое, что , и это решение единственное.   УРП (Дифференциальные уравнения 1-ого порядка с разделяющимися переменными). - УРП, если . 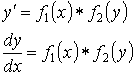- разделение переменных - общее решение данного дифференциального уравнения. 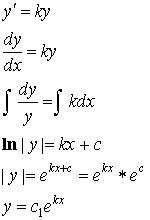Пример: Однородное уравнение 1-ого порядка. - называется однородным если функция , является однородной функцией, нулевого измерения. 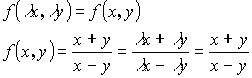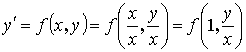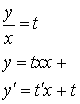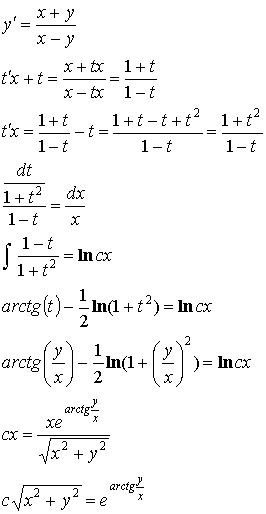- однородная функция n-ого измерения если (0-е измерение) (2-ого порядка) (неоднородная) Введем новую функцию: Уравнение примет вид: - уравнение с разделяющимися переменными Пример: Линейные уравнение 1-ого порядка и их решение Уравнение называется линейным, если его можно записать в следующем виде: , где и - произвольные функции от . - линейное уравнение без правой части. 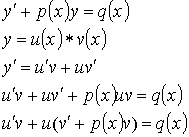Два метода решения линейных уравнений: Метод Бернулли Метод Лагранжа (вариации произвольной постоянной) Метод Бернулли: замена неизвестной функции y(x) на произведение двух неизвестных функций Выберем так, чтобы . Метод Лагранжа: - уравнение без правой части. (2) - удовлетворяет уравнению (2). Пример: 1) 2)

назад | оглавление | вперёд