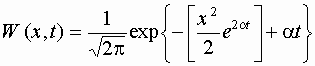СЛУЧАЙНЫЕ ПРОЦЕССЫ. ФУНКЦИИ РАСПРЕДЕЛЕНИЯ И ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ

Цель занятия: Изучение вероятностных характеристик (законов распределения вероятностей), числовых характеристик и свойств случайных сигналов и помех в каналах и системах связи.

Литература:

[ 1 ] – стр. 28 – 38;
[ 2 ] – стр. 166 – 189;
[ 3 ] – стр. 161 – 172;
[ 4 ] – стр. 8 – 10;
[ 5 ] – стр. 133 – 138, 154 – 157.

Контрольные вопросы

1. Что называется случайной функцией?
2. Что называется случайным процессом?
3. Что называется реализацией случайного процесса? Примеры реализаций случайного процесса?
4. Что такое сечение случайного процесса? Что представляет собой случайный процесс в сечении?
5. Как определяется одномерная плотность распределения вероятностей случайного процесса? Что она показывает?
6. Что такое n-мерные функции распределения случайного процесса ? Зачем они нужны при описании случайных процессов?
7. Какой процесс называют чисто случайным? Как связаны n-мерная и одномерная функции распределения чисто случайного процесса?
8. Какие процессы называются марковскими? Какие функции распределения вероятностей используются для их описания?
9. Что называется математическим ожиданием, дисперсией и корреляционной функцией случайного процесса?
10. Что такое нормированная корреляционная функция и интервал корреляции? Как они вычисляются?
11. Какие случайные процессы называются стационарными в узком смысле? Какие в широком?
12. Чему равняется значение функции корреляции стационарного случайного процесса B(t ) при t = 0 ?
13. Какие случайные процессы называются взаимно стационарными?
14. Чем отличается некоррелированность от независимости сечений случайных процессов?
15. Какие процессы называются эргодическими?
16. Как определяются числовые характеристики эргодического случайного процесса?
17. Как используется понятие эргодичности случайных процессов в инженерной практике? Примеры.

Задачи

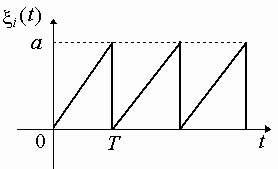
7.1*. Построить график одномерной плотности распределения вероятности случайного напряжения, реализация которого показана на рис. 7.1.

Определить математическое ожидание и дисперсию усреднением по времени одной реализации и усреднением по множеству реализаций.

1	2	3	4	5	6	7	8
c=2	c=1	c=0	c=–2	c=–1	T1=T2	T1=2T2	T1=0,5T2

7.2. Флуктуационные помехи x и h , воздействующие на сигнал в канале связи, некоррелированы имеют гауссовские законы распределения с параметрами mx , s 2x и mh , s 2h соответственно.

Определить их совместную плотность вероятности.

7.3. На рис. 7.2 изображены графики математического ожидания m(t) дисперсии s 2(t) для трех разновидностей случайной помехи, действующей в канале связи: x(t); y(t); z(t). Указать на графике области возможных значений каждой из случайной помехи, считая, что границы этих областей определяются значениями s 2(t).

таблица 7.2

7.4. Известно, что в любой момент времени t распределение случайной помехи x в канале связи определяется законом:

.

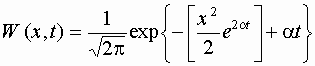Определить математическое ожидание m(t) и дисперсию s 2(t); изобразить на графике возможную область значений случайного процесса x(t), считая, что границы этой области соответствуют 3s . Изобразить также схематически деформацию закона распределения W(x) во времени для трех моментов, для которых a t1 = 0, a t2 = 1, a t3 = 3.

7.5. Показать, что если два случайных сигнала x(t) на входе и y(t) на выходе приёмного устройства в результате преобразований в приемном устройстве связаны линейной зависимостью y = a ± bx, то нормированная корреляционная функция rxy = ± 1.

7.6. Найти одномерную W1(x 1,t) и двумерную W2(x 1,x 2,t1,t2) плотности распределения вероятностей случайного сигнала, приходящего на приемную антенну тропосферной линии связи, если

x (t) = a cosw t + b sinw t,

где w – постоянная угловая частота,

a и b – взаимно независимые случайные величины с
нулевыми средними значениями ma = mb = 0
и дисперсиями s 2a = s 2b = s 2.

7.7*. Определить постоянную составляющую, среднюю мощность переменной составляющей и функцию корреляции реализаций случайных сигналов, передаваемых в многоканальной системе связи:

1) x i (t) = asinw 0t, 2) x i(t) = acosw 0t,

3) x i(t) = asin(w 0t + j ), 4) x i(t) = acos(w 0t + j ),

5) x i(t) = a[1 + sinw 0t], 6) x i(t) = a[1 + cosw 0],

где j – случайная фаза с равномерным законом распределения

.

7.8**. Найти корреляционную функцию B(t ) и интервал корреляции t 0 случайного синхронного телеграфного сигнала, реализации которого имеют случайный равномерно распределенный сдвиг D t относительно начала координат, принимающий в дискретные моменты времени кратные T значения ± A с вероятностью 0,5 независимо от того, какое значение он имел на предыдущем участке (рис. 7.3, а), и одиночной телеграфной посылки (рис. 7.3, б).

7.9. Показать, что взаимная корреляционная функция Bxy(t,t¢ ) стационарной случайной помехи x(t) и , полученной в результате прохождения x(t) через дифференцирующую цепь, удовлетворяет условию:

Bxy(t, t¢ ) = – Bxy(t¢ , t),

т.е. при перемене местами аргументов меняется знак.

7.10. Флуктуационная помеха x в канале связи распределена по гауссовскому закону с характеристиками mx и s x. После прохождения двух параллельных приемных трактов многоканальной системы связи образуются случайные помехи y и z, связанные с x зависимостями y = x2 ; z = x3. Найти взаимные корреляционные функции Bxy, Bxz, Byz.

7.11**. Найти корреляционную функцию, ковариационную функцию, нормированную корреляционную функцию и интервал корреляции t 0 случайного стационарного телеграфного сигнала x(t), изображённого на рис 7.4 и представляющего собой последовательность прямоугольных импульсов равной амплитуды (равной 1) и случайной длительности. Распределения переходов (1® 0 и 0® 1) принимаются независимыми, т.е. распределение значений x(t) (или 0, или 1) подчиняется закону Пуассона.

7.12**. Найти корреляционную функцию дискретного случайного стационарного телеграфного сигнала x(t), изображённого на рис. 7.5. Известно, что случайная величина x(t) может принимать значения +1 и –1 с равной вероятностью, а вероятность независимых перемен знака определяется законом Пуассона (см. 7.11).

Задачу решить независимо от предыдущей; полученный результат сопоставить с результатом решения предыдущей задачи и показать возможность решения данной задачи на основе использования результата предыдущей.

7.13**. Случайный сигнал x(t) рис. 7.6 для передачи по каналу связи дискретизирован по уровню. Известно, что число перемен знака подчиняется закону Пуассона (см. 7.11), кроме того, M{xi}=0, где xi – значение случайной величины на текущем интервале между переменами знака, считаются независимыми. Задано, кроме того, M{xi2}.

Найти корреляционную функцию.

7.14*. Даны корреляционные функции (рис. 7.7) случайных сигналов, передаваемых по каналу связи.

Найти интервал корреляции t 0 для указанных корреляционных функций.

7.15. Найти корреляционную функцию периодического сигнала многоканальной системы связи, представленного рядом Фурье:

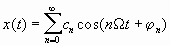
7.16. Найти функцию взаимной корреляции сигнала x1(t) произвольной формы и “узкого импульса”, который может быть представлен функцией x2(t) = x0 d (t – t0).

7.17. Найти функцию взаимной корреляции двух зондирующих “узких” импульсов в гидроакустическом канале связи, сдвинутых между собою на время D t.

7.18. Найти взаимную корреляционную функцию радиолокационных сигналов: периодической последовательности “узких” импульсов и сигнала x1 (t) произвольной формы и с ограниченной длительностью.

7.19. Найти взаимную корреляционную функцию измерительных сигналов x1 (t) и x2 (t), изображённых на рис. 7.8:

7.20. На вход приемника системы связи поступает слабый “периоди-ческий на отрезке” сигнал

x(t) = acos(w t + j ), (0 < t < s )

вместе с шумом, корреляционная функция которого имеет вид :

Сформулировать условия, при которых возможен приём слабого сигнала x(t) и составить структурную схему приемника. Считается, что сигнал и шум между собой некоррелированы.

7.21. Вычислить и изобразить графически корреляционную функцию одиночной кодовой последовательности прямоугольных импульсов длительности t вида:

Вычислить корреляционную функцию этих же последовательностей при периодическом повторении и сравнить с функцией корреляции одиночной последовательности.

7.22. Плотность вероятности двух случайных сигналов X и Y в канале связи выражается формулой :

W2(x,y) = Asin(x + y), (0 £ x £ p /2, 0 £ y £ p /2).

Определить постоянную A, затем найти функции распределения вероятностей: F2 (x,y), F1 (x), F1 (y).

7.23. По законам распределения, найденным в предыдущей задаче, найти вероятности, соответствующие следующим условиям:

7.24. Передаются два случайных сигнала X и Y, известна связь между ними и случайным параметром j :

x = сosj ; y = sinj .

Случайный параметр j распределен равномерно в интервале
[–p ; p ]. Найти нормированную корреляционную функцию rxy(D j ).

7.25. Случайная помеха в канале связи характеризуется гауссовским распределением мгновенных значений

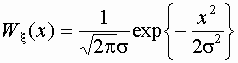
Найти закон распределения помехи z = x1 – x2, если x1 и x2 мгновенные значения помехи, являющиеся по условию независимыми случайными величинами.

7.26 Задана плотность распределения вероятностей двух случайных сигналов x(t) и y(t):

W2(x,y) = 0,5 sin(x+y), (0 £ x £ p /2 ; 0 £ y £ p /2).

Найти математическое ожидание, дисперсию, функцию взаимной корреляции случайных сигналов X и Y, построить корреляционную и нормированную корреляционную матрицы.

7.27. Заданы сигналы y1 и y2, которые образуются в результате преобразования сигналов x1 и x2 в канале связи:

y1 = ax1 + bx2 ; y2 = (x1 + x2)*2 ;

Найти Якобиан и установить, являются ли сигналы y1 и y2 независимыми.

Примечание: Для аудиторной работы с подробным анализом результатов решения рекомендуются задачи 7.1, 7.3, 7.8, 7.21. обратить внимание на возможность применения выводов из результатов решения задач 7.8 и 7.21 для повышения помехоустойчивости систем связи.

* При решении задач, отмеченных *, рекомендуется составить программу на алгоритмическом языке ЭВМ.

** Решение задач, отмеченных **, рекомендуется проиллюстрировать структурной схемой алгоритма.

назад | оглавление | вперёд