СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ СЛУЧАЙНОГО ПРОЦЕССА.
УЗКОПОЛОСНЫЕ И ШИРОКОПОЛОСНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ

Цель занятия: Овладение методами корреляционного и спектрального анализа случайных сигналов и помех в системах связи.

Литература:

[ 1 ] – стр. 36 – 57;
[ 2 ] – стр. 193 – 200, 202 – 212;
[ 3 ] – стр. 165 – 167, 252 – 256;
[ 4 ] – стр. 8 – 12.

Контрольные вопросы

1. Что такое энергетический спектр стационарного случайного процесса? Как он связан с корреляционной функцией?
2. Как определяется эффективная ширина энергетического спектра случайного процесса?
3. Как связаны интервал корреляции и эффективная ширина спектра случайного сигнала?
4. Какие процессы называются узкополосными, какие широкополосными?
5. Что такое “белый шум”? Его свойства?
6. Как определяется корреляционная функция узкополосного случайного процесса?
7. Что такое аналитический сигнал?
8. Что такое огибающая E(t) и начальная фаза j (t) узкополосного случайного процесса? как они связаны с квадратурными составляющими A(t) и B(t) ?
9. Какой закон распределения имеют квадратурные составляющие A(t) и B(t) узкополосного случайного процесса?
10. Какова средняя мощность случайных амплитуд A(t), B(t) и E(t) ?
11. Чему равна нормированная корреляционная функция квадратурных составляющих A(t) и B(t) rAB в совпадающие моменты времени?
12. Как определить совместную функцию плотности распределения квадратурных составляющих A(t) и B(t) узкополосного гауссовского процесса?
13. Какой закон распределения имеют значения огибающей гауссовского случайного процесса, когда:
    • математическое ожидание равно нулю;
    • математическое ожидание не равно нулю?
14. Какой закон распределения имеют значения начальной фазы гауссовского случайного процесса с нулевым математическим ожиданием?

Задачи

8.1*. Определить спектральную плотность случайного телеграфного сигнала x (t), если его функция корреляции имеет вид:

а) (получена в задаче 7.12);

б)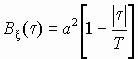 (получена в задаче 7.8);

8.2. На рис.8.1 изображены реализации помех 1(t) и 2(t).

Построить качественно их корреляционные функции и спектральные плотности.

8.3. Рассматривается случайная гармоническая помеха

где W – центрированная амплитуда с дисперсией DW ;

q – случайная фаза, распределенная равномерно в интервале (0, 2p );

w 1 – неслучайный параметр (w 1 > 0).

Случайные величины w и q независимы. Найти характеристики случайной помехи x(t): математическое ожидание, корреляционную функцию. Определить, является ли случайная гармоническая помеха x(t) стационарной и эргодической. Если она стационарна, то найти ее спектральную плотность Gx (w ).

8.4. Рассматривается случайный сигнал на входе приемника, полученный путем сложения от n антенн

,

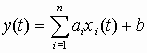где xi (t) – стационарные некоррелированные случайные сигналы
с характеристиками mi ; Bi (t ); Gi (w ), (i = 1, 2, ..., n);

ai , b – действительные числа.

Найти характеристики случайного сигнала y(t).

8.5. Рассматривается сложная мультипликативная помеха:

,

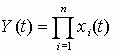где xi (t) – независимые стационарные случайные процессы

с характеристиками mi =0; B i (t ); G i (w ), (i = 1, 2, ..., n).

Найти характеристики помехи Y(t).

8.6. Определить, обладает ли функция

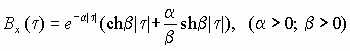
принятого неизвестного сигнала X(t) свойствами корреляционной функции.

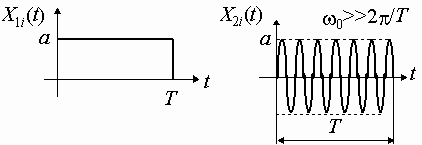
8.7*. Определить и построить графики функций корреляции, спектральных плотностей, вычислить интервалы корреляции и эффективную ширину спектров случайных сигналов X1(t) и X2 (t), реализации которых имеют вид (рис.8.2):

8.8*. Спектральная плотность G(w ) стационарного случайного сигнала X(t) имеет вид

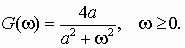
Определить соотношение между эффективной шириной спектра сигнала D w эф и шириной его спектра на уровне 0,5 G(0).

8.9**. Найти корреляционную функцию B(t ) стационарного случайного процесса с равномерной спектральной плотностью:

a) ; –¥ < w < ¥ – “белый” шум ;

б) 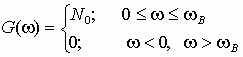– широкополосный процесс;

в)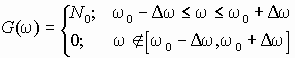

– узкополосный процесс.

8.10*. Спектральная плотность речевого сигнала G(w ) на различных участках фразы имеет вид:

а) , w ³ 0;

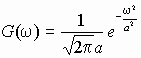б) , w ³ 0;

в) G(w )=2e–aw , a>0, w ³ 0;

г) G(w )=2w , 0 £ w £ w в.

Найти корреляционные функции. Построить графики G(w ) и B(t ).

8.11*. Выяснить разницу между спектральными плотностями случайных сигналов X1(t) и X2(t), передаваемых по каналам связи. Корреляционные функции B1(t ) и B2(t ) имеют вид:

а) B1(t )=B(0) e- a ½ t ½ , a >0,

B2(t )=B(0) e- a ½ t ½ cosw 0t , a > 0, w > > 2p /T;

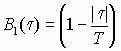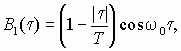б) , 0 £ t £ T;

0 £ t £ T

в) B1 (t ) = B(0) exp (- b 2 t 2),

B2 (t ) = B(0) exp (- b 2 t 2) cosw 0t ;

г) B1 (t ) = B(0), |t | £ t 0,

B2 (t ) = B(0)cosw 0t , |t | £ t 0, w 0 >>2p /Т.

8.12. Показать, что спектральная плотность случайного стационарного сигнала Y(t) с корреляционной функцией

By(t ) = Bx(t ) cosw 0t

определяется на положительных частотах ( при f0>>FЭ, где FЭ – ширина спектра сигнала с корреляционной функцией Bx(t) ) соотношением

Gy(f) = Gx(f – f0),

где Gx(f) – спектральная плотность стационарного сигнала с корреляционной функцией Bx(t ).

8.13. Показать, что изменение в a раз масштаба аргумента корреляционной функции в приемнике системы связи влечет за собой изменение спектральной плотности в соответствии с равенством

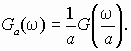
8.14. Найти спектральную плотность детерминированного процесса (элемента сигнала дискретной фазовой модуляции)

x(t) = a cos(w 0t + j 0), (0 £ t £ T)

и дать соответствующие спектральные диаграммы.

8.15. Найти спектральную плотность детерминированного финитного сигнала (элемента сигнала дискретной фазовой модуляции)

x(t) = a cos(w 0t + j 0); (0 £ t £ T),

полагая длительность T достаточной для того, чтобы считать приемлемой аппроксимацию корреляционной функции выражением:

B(t )=(a2/2)cosw 0t .

8.16. Найти спектральную плотность стационарной случайной помехи, действующей на сигнал. Корреляционная функция помехи определяется выражением:

B(t) = a ea ½ t ½ |2d (t )–a (signt )2 |.

8.17. Имеется стационарный случайный сигнал x(t) с корреляционной функцией

B(t) = (sint )/t .

Найти корреляционную функцию, дисперсию и спектральную плотность его производной y(t)= dx(t)/dt, полученной на выходе дифференцирующей цепи.

8.18. Случайный сигнал x(t) имеет корреляционную функцию

Bx (t) = ea ½ t ½ (chb |t |+(a /b )shb |t |), (a > 0, b > 0).

Случайный сигнал на выходе дифференцирующего устройства равен y(t)=dx(t)/dt. Найти его корреляционную функцию By(t ) и спектральную плотность Gy(w ).

8.19. Найти спектральную плотность марковского гауссовского процесса, для которого нормированная функция корреляции равна

r(t ) = a ea ½ t ½ e–a |t |.

8.20. Найти спектральную плотность квазислучайного фототелеграфного сигнала, имеющего закон распределения

Wx(t) = (l t)2k sech l t½ 2k½ , (k = 0,1,2,...)

и нормированную корреляционную функцию

r(t) = sech(l t ) cos(l t ).

8.21.** Известно, что плотности распределения вероятностей мгновенных значений флуктуационной помехи в двух независимых сечениях x и y являются гауссовскими с нулевыми математическими ожиданиями и одинаковыми дисперсиями, т.е.

;

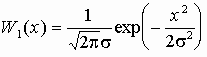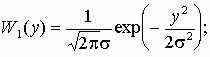
ax = 0 ; ay = 0 ; s x = s y = s .

Рассматривая x и y как координаты точки в декартовой системе, найти законы распределения E и j , т. е. модуля и фазы в полярной системе координат; связь между случайными переменными известна:

x = E cosj ; y = E sinj .

8.22. Показать, что огибающую аналитического сигнала Sa(t) можно находить по формуле:

,

где – функция, комплексно сопряжённая к функции Sа(t);

8.23. Доказать следующие свойства аналитического сигнала:

Sa (t) = S(t) = E(t), если

, если

E(t)³ S(t).

8.24. Преобразовать по Гильберту сигналы дискретной фазовой модуляции x(t) = a cosw 0t и x(t) = a sinw 0t.

8.25. Для сигнала дискретной амплитудной модуляции x(t)=ai cosw 0t, (ai = 0, 1) построить аналитический сигнал xа(t).

8.26. Дан непериодический сигнал x(t), имеющий спектральную функцию S(jw ). Допустим, что построен сигнал , у которого спектр “повернут” на p /2, т.е. спектральная функция сигнала определяется выражением

S(jw ) = S(jw )exp{–j(p /2) signw },

где sign w = 1, если w > 0 и sign w = –1, если w < 0.

Найти связь между x(t) и во временной области.

8.27**. Сигнал многоканальной системы связи представлен в виде:

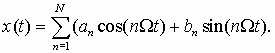
Записать этот сигнал в виде огибающей и фазы

x(t) = E(t) cosy (t).

8.28**. Дана гармоническая помеха

x(t) = a1сosw 1t + a2сosw 2t,

представить ее в виде

x(t) = E(t) cos(w t + q (t) + j 0),

сначала для частоты w =w 1, затем для частоты w =w 0, где w 0 = (w 1 + w 2)/2.

Решение провести двумя способами. По первому способу получить решение, не прибегая к понятию аналитического сигнала, т.е. выполняя известные операции сложения гармонических колебаний; по второму – с использованием понятия аналитического сигнала.

8.29**. Дан сигнал , являющийся типичным примером сигнала в многоканальных системах связи. Получить выражение аналитического сигнала в общем виде, а затем для частного случая cn = c, j n = j . Линейный член выделить по отношению к средней частоте w ср = w 0 + [(N+1)/2]W .

8.30. Сигнал x(t) задан своей спектральной плотностью вида:

S(jw ) = S1(w ) – jS2(w ) = 1, (w 1 < w < w 2),

постоянной в диапазоне частот от w 1 до w 2. Найти временную запись сигнала x(t) и затем представить ее в форме аналитического сигнала. Рассмотреть частный случай при w 1 = 0.

Примечание: Для аудиторной работы с подробным анализом результатов решения рекомендуются задачи: 8.1, 8.7, 8.9. Следует обратить внимание на связь временной реализации случайного процесса со спектральной плотностью и корреляционной функцией, интервала корреляции с эффективной шириной спектра, на изменение корреляционной функции и спектральной плотности при переходе от реализации сигнала видеоимпульса к радиоимпульсу, а так же на корреляционные функции узкополосных случайных процессов.

* При решении задач, отмеченных *, рекомендуется составить программу вычислений на алгоритмическом языке ЭВМ.

** При решении задач, отмеченных **, решение рекомендуется проиллюстрировать структурной схемой алгоритма.

назад | оглавление | вперёд