Теория электрической связи 

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №9

назад | оглавление | вперёд

  

ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ СИГНАЛОВ В РАДИОТЕХНИЧЕСКИХ УСТРОЙСТВАХ

Цель занятия: Изучение качественных и количественных изменений характеристик случайных сигналов и помех в линейных и нелинейных электрических цепях различного вида.

Литература:

[ 1 ] – стр. 86 – 89;
[ 2 ] – стр. 299 – 310, 347 – 354;
[ 3 ] – стр. 268 – 288.

Контрольные вопросы

  1. Как классифицируются радиотехнические устройства при решении задач преобразования случайных сигналов этими устройствами?
  2. Какие два типа задач решаются при анализе результатов преобразования случайных сигналов радиотехническими устройствами?
  3. В чем отличие линейных радиотехнических устройств с постоянными и переменными параметрами?
  4. Каким образом связаны импульсная и передаточная характеристики линейного радиотехнического устройства?
  5. Как определяется временная функция сигнала на выходе линейного инерционного устройства?
  6. Чем объяснить нормализацию случайного сигнала на выходе линейного инерционного радиотехнического устройства при воздействии на его вход произвольного случайного сигнала?
  7. Как определяется энергетический спектр и функция корреляции сигнала на выходе линейного инерционного устройства?
  8. Как изменяются свойства случайного сигнала (шума) с нормальным законом распределения в результате его преобразования в линейном устройстве?
  9. Как определяется закон распределения случайных величин, функционально связанных с другими случайными величинами, закон распределения которых известен?
  10. Как определяется временная функция сигнала на выходе нелинейного безынерционного устройства?
  11. Каким образом определяется одномерная и n–мерная плотность распределения вероятностей случайного сигнала на выходе нелинейного
    безынерционного устройства?

Задачи

1

2

3

4

5

6

K(w )=A,
w –D w £ w £ w +D w ;
K(w )=0,
w –D w > w >w +D w

7

8

K(w )=A, 0 £ w £ w в;
K(w )=0, w >w в

9.1**. На электрическую цепь, показанную на рис. 9.1, воздействует белый шум x (t). Определить и построить график энергетического спектра и функцию корреляции шума y(t) на выходе. Найти дисперсию шума на выходе устройства.

9.2**. На вход дифференциального устройства поступает случайный сигнал x (t) с математическим ожиданием mx (t) = sin(t) и корреляционной функцией

Bx (t1, t2) = s 2x exp{–a (t1 – t2)2}

Определить математическое ожидание, функцию корреляции и дисперсию на выходе устройства.

9.3. Случайный сигнал, корреляционная функция которого

B(t ) = exp(–at ),

воздействует на вход линейного инерционного устройства с АЧХ:

.

Определить и построить график корреляционной функции на выходе устройства.

9.4. Определить и построить график распределения случайного сигнала на выходе:

а) линейного детектора огибающей;

б) квадратичного детектора огибающей, когда на входе действует случайный сигнал, представляющий собой гауссовский процесс с нулевым математическим ожиданием.

9.5. На вход безынерционного устройства, характеристика которого показана на рис. 9.2, действует стационарный гауссовский шум x(t) с нулевым математическим ожиданием. Определить плотность распределения вероятностей W(y) шума y(t) на выходе устройства.

9.6. Показать, что при квадратичном преобразовании y = ax2 стационарного гауссовского шума, двумерная плотность распределения вероятностей которого имеет вид:

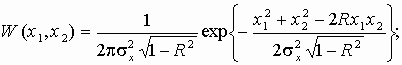
коэффициент корреляции шума на выходе равен квадрату коэффициента корреляции входного шума. Как изменяется средняя мощность процесса?

9.7**. На приёмное устройство, состоящее из усилителя промежуточной частоты (УПЧ), квадратичного детектора огибающей и RC–фильтра нижних частот воздействует стационарный белый шум x (t) со спектральной плотностью Gx (w ) = N0. Передаточная функция УПЧ имеет вид:

а импульсная функция g(t) фильтра нижних частот равна

g(t) = g e–g t.

1

y = ax 2

2

y = ax 2,
x ³ 0; a > 0

3

y = ax ,
x ³ 0; a > 0

4

y = b , x > a ;
y = ax , 0 £ x £ a ;

5

y = ax , x ³ a
y = 0, x < a

6

y = –b , x < –a ;
y= a x , – a £ x £ a ;

7

y = b , x ³ 0;
y = –b , x < 0;

8

y= b , x > a ;
y = 0, –a £ x £ a
y = –b , x < –a

Определить :

а) плотность распределения вероятности W(h ) шума h (t) на выходе квадратичного детектора огибающей, а также среднее значение mh , функцию корреляции Bh (t ) и дисперсию s 2h ;

б) среднее значение my, функцию корреляции By(t ) и дисперсию s 2y на выходе RC–фильтра нижних частот.

9.8. Плотность распределения амплитуды сигнала на выходе канала связи с замираниями имеет вид (закон Релея)

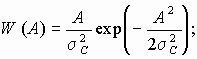
где s с2 – средняя мощность сигнала.

Определить и построить плотности распределения отношения сигнал/шум W(h) и W(h2), учитывая, что величины h2 и A связаны функциональной зависимостью h2 = A2/(2s п2), где s п2 – средняя мощность шума на выходе канала связи.

9.9. На вход дифференцирующего устройства поступает случайный сигнал x (t) с математическим ожиданием mx (t)=sint и корреляционной функцией Bx (t1,t2) = s x 2exp[–a (t2–t1)].

Определить математическое ожидание, функцию корреляции и дисперсию на выходе устройства.

Примечание: Для аудиторной работы с подробным анализом результатов решения могут быть рекомендованы задачи 9.1, 9.2, 9.5, 9.6, позволяющие выяснить влияние линейных инерционных и нелинейных безынерционных преобразований на функцию корреляции и спектр случайного сигнала.

** Решение задач, отмеченных **, рекомендуется проиллюстрировать структурной схемой алгоритма.

назад | оглавление | вперёд