Лекция №6

                     -  обобщенный ряд Фурье.

      Обобщенный ряд Фурье представляет собой некоторый сигнал относительно полного ортонормированного базиса.

Пример:

Аппаратурная реализация спектрального анализа

Рис. Анализатор спектра.

Ошибка аппроксимации зависит от числа ветвей.

Замечание по поводу полноты базиса Фурье

 - этот базис является полным .

Замечание: реальные сигналы всегда удовлетворяют условиям Дирихле.

      Если t – вне интервала (-T/2 , T/2) , то будет описывать периодическую функцию.

Непрерывное (интегральное ) представление сигналов

           Счетный базис                                      ядро интегрированного представления

i – дискретная переменная

            Спектр                                                        спектральная плотность

  - функция из зависимого базиса

 - сопряженное ядро

Условие самосопряженности базиса

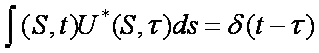
для ортонормированного базиса                        для самосопряженного ядра

Пример:

 - самосопряженное ядро

 - обратное преобразование Фурье

  - прямое преобразование Фурье

- обобщенная формула Релея представления сигналов через преобразование Фурье

Пример:

          - самосопряженное ядро

        Функция, которая линейна, называется сигналом x(t), фактически является спектральной плотностью сигнала относительно самосопряженного ядра